 |
Главная |
Пределпроизведениясходящихсячисловыхпоследовательностей
|
из
5.00
|
Произведениесходящихсяпоследовательностейестьсходящаясяпоследовательность, пределкоторойравенпроизведениюпределовпоследовательностей {xn} и {yn}.
Доказательство. Пустьa и b – естьсоответственнопределыпоследовательностей {xn} и {yn}.Тогдапоопределению
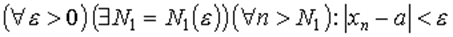

ВыберемM = max {N1, N2} длятого, чтобынеравенствавыполнялись, начиная с одного и тогожеN. Рассмотримразность
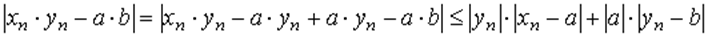 .
.
Таккакпоследовательностьуnимеетконечныйпредел, тоонаограничена и поэтомусуществуеттакоеположительноечислоA, чтодляn > Nбудетвыполнено | yn | <A. И поэтомуабсолютнаявеличинаразности

можетбытьсделанокакугодномалой, начиная с некоторогономераN. Этоозначает, чтопоследовательность {xn·yn} сходится и имеетсвоимпределомчислоa·b.
17) Теорема о переходе к пределу в неравенствах.
Пусть функции  и
и  имеют пределы
имеют пределы
А и В в точке  и
и  , для всех
, для всех  .
.
Тогда  .
.
18) Теорема о промежуточной последовательности.
Пусть  ,
,  ,
,  - две сходящиеся последовательности, причем
- две сходящиеся последовательности, причем 
 .Последовательность
.Последовательность  удовлетворяет неравенству :
удовлетворяет неравенству :  .
.
Тогда 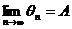 .
.
21. (замечательный предел)
Последовательность  имеет предел, равный числу e=2,71….
имеет предел, равный числу e=2,71….
ДОК. Напомним формулу бинома Ньютона:  , где
, где  - коэффициенты бинома. Применим формулу для
- коэффициенты бинома. Применим формулу для 

 . При увеличении n число слагаемых в сумме увеличивается, а каждое слагаемое также увеличивается, т.е.
. При увеличении n число слагаемых в сумме увеличивается, а каждое слагаемое также увеличивается, т.е.  монотонно возрастающая последовательность. Докажем ее ограниченность сверху.
монотонно возрастающая последовательность. Докажем ее ограниченность сверху.

Тогда по теореме  имеет предел.
имеет предел.
УПРАЖНЕНИЯ. (1) Доказать, что если последовательность  сходящаяся, то последовательность
сходящаяся, то последовательность  также сходящаяся. (2) Справедливо ли утверждение : сумма двух бесконечно больших
также сходящаяся. (2) Справедливо ли утверждение : сумма двух бесконечно больших
последовательностей является бесконечно большой последовательностью ? (обосновать) (3) Доказать, что произведение двух бесконечно больших последовательностей есть бесконечно большая последовательность.
Рассмотрим функцию  и точку
и точку  такую, что
такую, что  . В частности, точка
. В частности, точка  может быть внутренней точкой для E :
может быть внутренней точкой для E :  .
.
ОПР.(КОШИ) Число А называется пределом функции  в точке
в точке  , обозначение
, обозначение  , если
, если 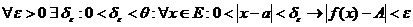 .
.
ОПР.(ГЕЙНЕ) Число А называется пределом функции  в точке
в точке  , обозначение
, обозначение  , если
, если 
Множество V на числовой оси называется открытым, если 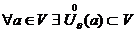 . Любое открытое множество V(a), содержащее точку a, называют окрестностью точки a.
. Любое открытое множество V(a), содержащее точку a, называют окрестностью точки a.
ОПР.(ТОПОЛОГИЧЕСКОЕ) Число А называется пределом функции  в точке
в точке  , обозначение
, обозначение  , если
, если
 .
.
ТЕОРЕМА 1 Определения по Гейне и по Коши предела функции в точке эквивалентны, т.е. если число А является пределом функции по Коши, то оно же является пределом по Гейне и
наоборот.
ДОК. (1) Пусть  по Коши :
по Коши : 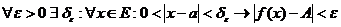 .
.
Пусть 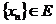 произвольная последовательность, для которой
произвольная последовательность, для которой  .Тогда
.Тогда  ,т.е.
,т.е. 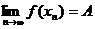 .
.
(2) Пусть  по Гейне.
по Гейне.
Предположим, что число А не является пределом функции  по Коши. Тогда
по Коши. Тогда  .
.
Построенная последовательность  сходящаяся и
сходящаяся и  . Тогда
. Тогда  . Полученное противоречие доказывает, что число А является пределом функции по Коши.
. Полученное противоречие доказывает, что число А является пределом функции по Коши.
ОПР. Функция  называется ограниченной в окрестности
называется ограниченной в окрестности  , если существует число М, для которого
, если существует число М, для которого
 .
.

23.Предел промежуточной функции
Если в некоторой окрестности точки х0 выполняется неравенство g (x) < f (x) < p (x) и

то

Доказательство. Так как

то
(  ε > 0 ) (
ε > 0 ) (  δ1 = δ1 (ε) > 0 ) (
δ1 = δ1 (ε) > 0 ) (  0 < | x - x0 | < δ1 ) : | g (x) – A | < ε
0 < | x - x0 | < δ1 ) : | g (x) – A | < ε
Так как
 ,
,
то
(  ε > 0 ) (
ε > 0 ) (  δ2 = δ2 (ε) > 0 ) (
δ2 = δ2 (ε) > 0 ) (  0 < | x - x0 | < δ2 ) : | p (x) – A | < ε
0 < | x - x0 | < δ2 ) : | p (x) – A | < ε
Пусть δ = min(δ1,δ2} то " 0 < |x - x0| < δ имеем
A– ε < g( x) < f ( x) < p( x) < A + ε
то есть
(  ε > 0 ) (
ε > 0 ) (  δ = δ (ε) > 0 ) (
δ = δ (ε) > 0 ) (  0 < | x - x0 | < δ ) : | f (x) – A | < ε.
0 < | x - x0 | < δ ) : | f (x) – A | < ε.
Это означает, что

24Предельный переход в неравенстве.
Пусть в некоторой выколотой δ – окрестности точки х0 функции f (x) и g (x) определены и выполнено неравенство f (x) < g (x). Пусть существуют пределы
 и
и 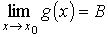
тогда справедливо неравенство А ≤ B.
Доказательство. Пусть это не так,пусть А > B. Выберем как угодно малое положительное число ε таким, чтобы окрестности точек А и В не пересекались
(A – ε; A + ε ) ∩ (B – ε; B + ε ) ) = Ø
Кроме того по предположению

Знак между интервалами означает, что интервал (A - ε; A + ε) лежит правее интервала (B - ε; B + ε).
Из существования пределов функций f (x) и g (x) в точке х0 следует
(  ε > 0 ) (
ε > 0 ) (  δ1 = δ1 (ε) > 0, δ1 < Δ) (
δ1 = δ1 (ε) > 0, δ1 < Δ) (  0 < | x - x0 | < δ1 ) : | f (x) – A | < ε,
0 < | x - x0 | < δ1 ) : | f (x) – A | < ε,
и
(  ε > 0 ) (
ε > 0 ) (  δ2 = δ2 (ε) > 0, δ2 < Δ) (
δ2 = δ2 (ε) > 0, δ2 < Δ) (  0 < | x - x0 | < δ2 ) : | g (x) – B | < ε,
0 < | x - x0 | < δ2 ) : | g (x) – B | < ε,
Если принять δ = min {δ1,δ2} < δ, то для 0 < | x - x0| < δ следует неравенство f (x) > g(x). Но это противоречит условию теоремы, значит, наше предположение А > B неверное.








№33
ТЕОРЕМА ( 1- я теорема Вейерштрасса)
Всякая непрерывная функция  на отрезке ограничена на этом отрезке.
на отрезке ограничена на этом отрезке.
ДОК. Предположим противное: функция  на отрезке [a;b] неограниченна ®
на отрезке [a;b] неограниченна ®  . Последовательность
. Последовательность  ограничена по построению, поэтому по теореме у нее есть предельная точка
ограничена по построению, поэтому по теореме у нее есть предельная точка  . Поскольку функция
. Поскольку функция  непрерывна в точке c, она ограничена в окрестности этой точки ( теорема об ограниченности функции, имеющей предел),
непрерывна в точке c, она ограничена в окрестности этой точки ( теорема об ограниченности функции, имеющей предел),
т.е.  . Тогда в окрестности
. Тогда в окрестности  может находиться не более конечного числа членов последовательности
может находиться не более конечного числа членов последовательности  , что противоречит тому, что c– предельная точка последовательности
, что противоречит тому, что c– предельная точка последовательности  .
.
Доказано, что множество  значений функции
значений функции  ограничено. Тогда по теореме о точной верхней и нижней грани существует
ограничено. Тогда по теореме о точной верхней и нижней грани существует  и
и  .
.
ОПР. Если 
 , то А называется наименьшим значением функции
, то А называется наименьшим значением функции  на отрезке [a;b].
на отрезке [a;b].
Обозначение  .
.
ОПР. Если 
 , то В называется наибольшим значением функции
, то В называется наибольшим значением функции  наотрезке [a;b].
наотрезке [a;b].
Обозначение  .
.
№34
ТЕОРЕМА .(2 – я теорема Вейерштрасса)
Непрерывная функция на отрезке принимает наименьшее и наибольшее значения.
ДОК. (1) Пусть  . Тогда, по определению точной нижней грани,
. Тогда, по определению точной нижней грани,  . Последовательность
. Последовательность  ограничена,поэтому у нее есть предельная точка c1
ограничена,поэтому у нее есть предельная точка c1  . Тогда у нее есть подпоследовательность
. Тогда у нее есть подпоследовательность 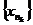 , для которой
, для которой  и по теореме о промежуточной последовательности
и по теореме о промежуточной последовательности  .
.
Поскольку функция  непрерывна в точке
непрерывна в точке  ,
,  , т.е.
, т.е. 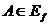 .
.
(2) Пусть  . Тогда, по определению точной верхней грани,
. Тогда, по определению точной верхней грани,  . Последовательность
. Последовательность  ограничена, поэтому у нее есть предельная точка c2
ограничена, поэтому у нее есть предельная точка c2  . Тогда у нее есть подпоследовательность
. Тогда у нее есть подпоследовательность 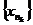 , для которой
, для которой 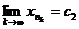 , и по теореме о промежуточной последовательности
, и по теореме о промежуточной последовательности  . Поскольку функция
. Поскольку функция  непрерывна в точке
непрерывна в точке  ,
,  , т.е.
, т.е.  .
.
35.Теорема о нуле непрерывной функции.
Теорема.
Пусть функция  непрерывна на отрезке
непрерывна на отрезке 
Тогда 
Д-во:
1.Разделим отрезок 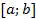 пополам, т.е.
пополам, т.е. 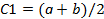 , если
, если  , то точку нашли.
, то точку нашли.
Если  , то выбираем один из полученных отрезков (либо [а;с1], либо [c1;b]), на концах которого значения функции разного знака.
, то выбираем один из полученных отрезков (либо [а;с1], либо [c1;b]), на концах которого значения функции разного знака.
2. Делим ещё раз и тд.
3. Получили последовательность вложенных отрезков, длина которых  0 , т.е. получили посл-ть стягивающихся отрезков.
0 , т.е. получили посл-ть стягивающихся отрезков.
По теореме о системе стягивающихся отрезков (существует точка С) 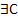 , которая принадлежит всем вложенным отрезкам, т.е. системе стягивающихся отрезков.
, которая принадлежит всем вложенным отрезкам, т.е. системе стягивающихся отрезков.
При этом, если  , то из непрерывности функции
, то из непрерывности функции  следует, что (существует некоторая окрестность точки C)
следует, что (существует некоторая окрестность точки C)  , в пределах которой
, в пределах которой  сохраняет знак, но это противоречит способу построения вложенных отрезков. Значит,
сохраняет знак, но это противоречит способу построения вложенных отрезков. Значит,  .
.
Теорема доказана.
36.Теорема о промежуточных значениях непрерывной функции.
Теорема.
Еслиф-ияf (x) непрерывна на отрезке [a;b]  , то для
, то для 
|
из
5.00
|
Обсуждение в статье: Пределпроизведениясходящихсячисловыхпоследовательностей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

