 |
Главная |
Реализация типовых задач на компьютере с помощью ППП Excel
|
из
5.00
|
ВВЕДЕНИЕ
Компьютерное моделирование экономических процессов становится не объемлемым элементом подготовки современного экономиста. Данное учебное пособие ориентировано на формирование у студентов навыков практического выполнения достаточно сложного комплекса расчетов по эконометрике и проведению с ними вычислительных экспериментов.
В учебно-методическом пособии рассмотрены вопросы построения экономико-математических моделей основных типов задач эконометрики и способы их решения средствами табличного редактора Microsoft Excel.
В пособие включены задания по всем темам, предусмотренных рабочей программой курса «Эконометрика». Задания по каждой теме содержат справочную информацию по расчетным формулам и методам, используемым при выполнении заданий. Чтобы облегчить понимание и ускорить овладение учебным материалом, в начале каждой темы приведено подробное решение типового задания с соответствующим выводом результатов. Навыки, полученные при решении типового задания, закрепляются в процессе самостоятельной работы над выполнением контрольного задания.
Задания практикума могут выполняться как с использованием Excel, так и любого статистического или эконометрического пакета (STATISTICA, SPSS, STATS, STATGRAPHICS). Однако автор предусмотрел выполнение компьютерных типовых задач в среде табличного процессора Excel, как наиболее известной и доступной.
ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ
Решение типовых задач
Пример 1.
По семи территориям Уральского района за 200Х г. известны значения двух признаков (таблица 1).
Таблица 1
Значения признаков по территориям Уральского района
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская республика | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Для характеристики зависимости у от х рассчитать параметры следующих функций: а) линейной; б) степенной; в) показательной; г) равносторонней гиперболы. Оценить каждую модель через среднюю ошибку аппроксимации А и F-критерий Фишера.
Решение
1а. Для расчета параметров a и b линейной регрессии у=a+bх решаем систему нормальных уравнений относительно а и b:
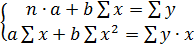 (1)
(1)
По исходным данным рассчитаем нужные неизвестные: ∑y, ∑x, ∑yx, ∑x², ∑y². Данные расчет представлены на рисунке 1 и 2.
b = 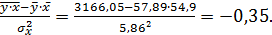
a = y̅ - b∙x̅ = 57,89-0,35∙54,9=76,9
Уравнение регрессии: 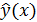 = 76,88 - 0,35х. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %. Рассчитаем линейный коэффициент парной корреляции:
= 76,88 - 0,35х. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %. Рассчитаем линейный коэффициент парной корреляции:
rxy = 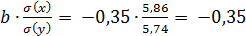 4
4
Связь умеренная, обратная.
Определим коэффициент детерминации:
r²xy = (-0,354)² = 0,125
Вариация результата на 12,5% объясняется вариацией фактора х. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения 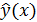 . Найдем величину средней ошибки аппроксимации
. Найдем величину средней ошибки аппроксимации 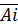 .
.
В среднем расчетные значения отклоняются от фактических на 8,1%.
Рассчитаем F-критерий:
Fфакт = 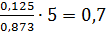
Поскольку 1 < F < ∞, следует рассмотреть 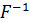
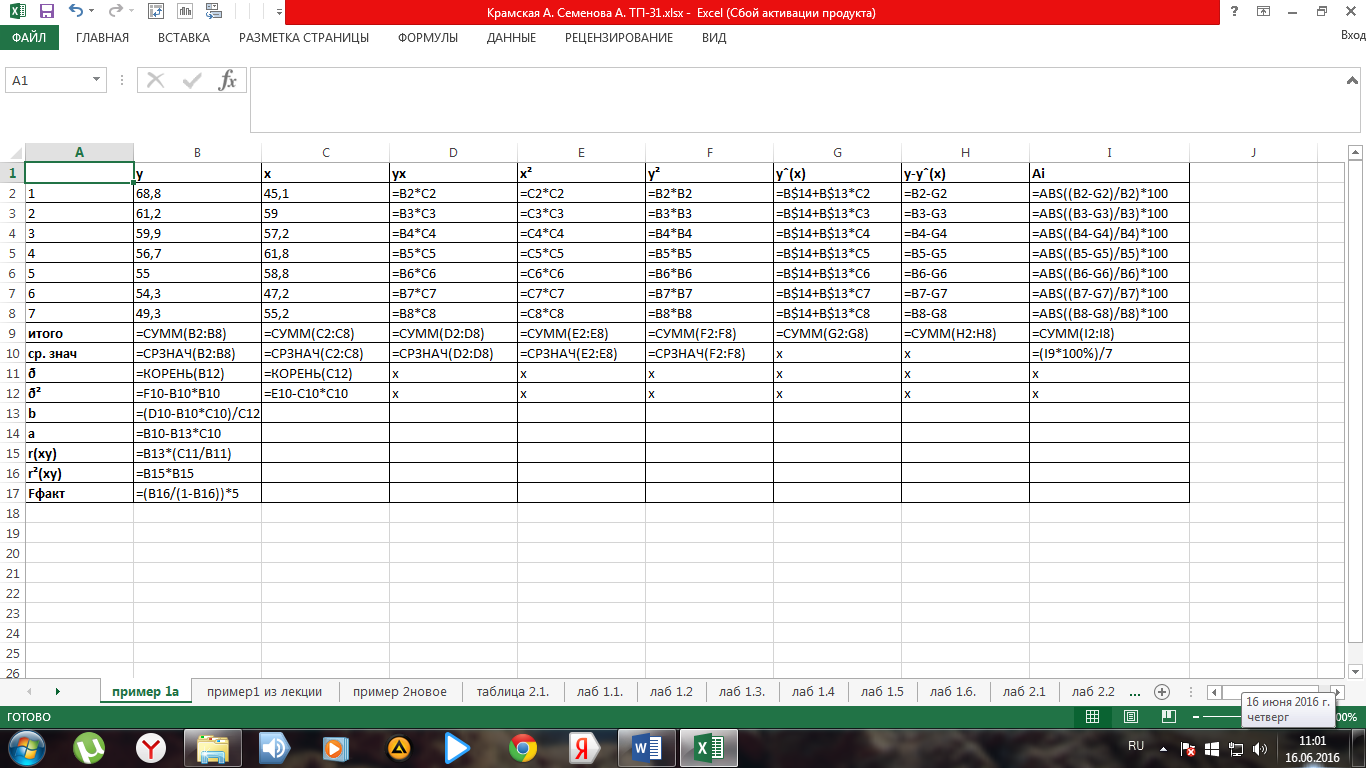
Рис. 1. Фрагмент листа электронной таблицы Microsoft Excel с расчетными формулами примера 1а
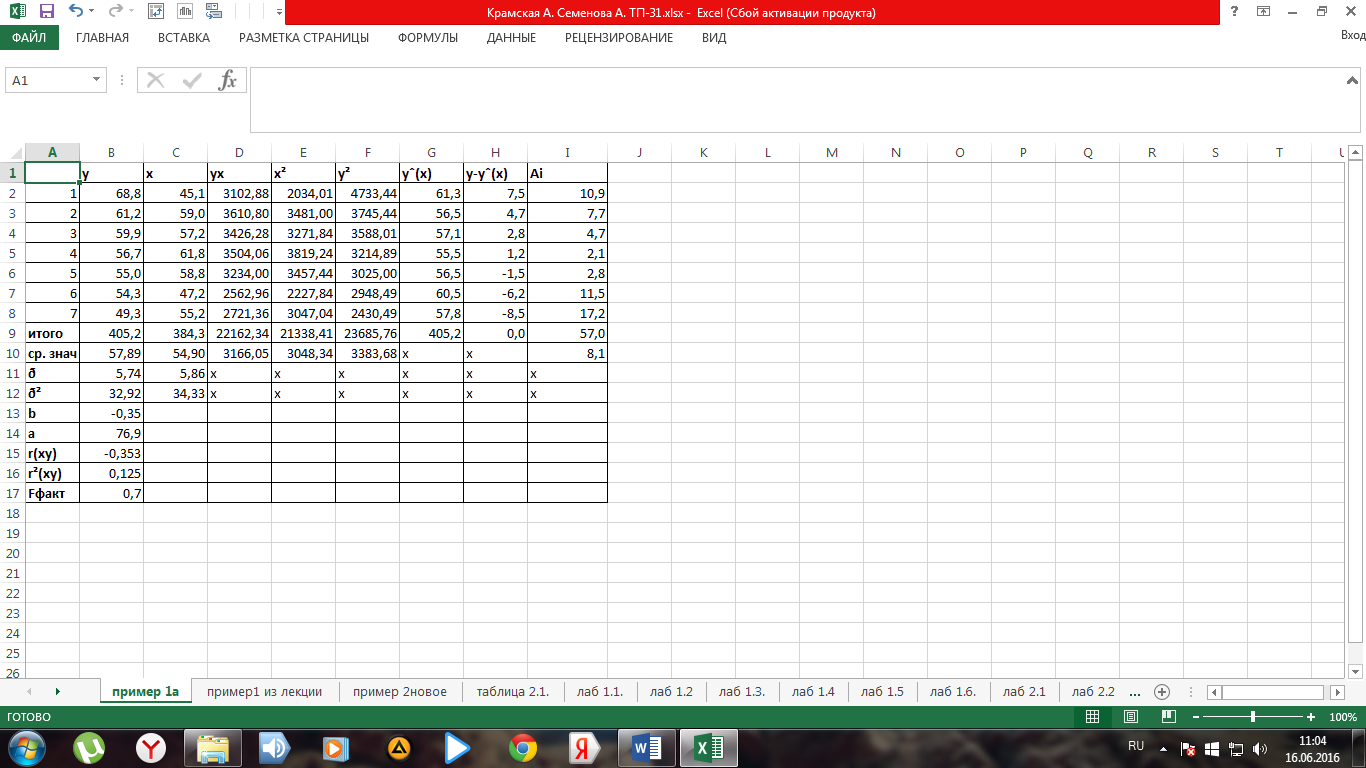
Рис. 2. Фрагмент листа электронной таблицы Microsoft Excel с решением примера 1а
Полученное значение указывает на необходимость принять гипотезу о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
1б. Построению степенной модели у = а∙ 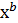 предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
lgy = lga + b∙1gx
Y = C + b∙X,
где Y=lg y, X=lg x, C = lg a.
Расчет представлен на рисунке 3 и 4.
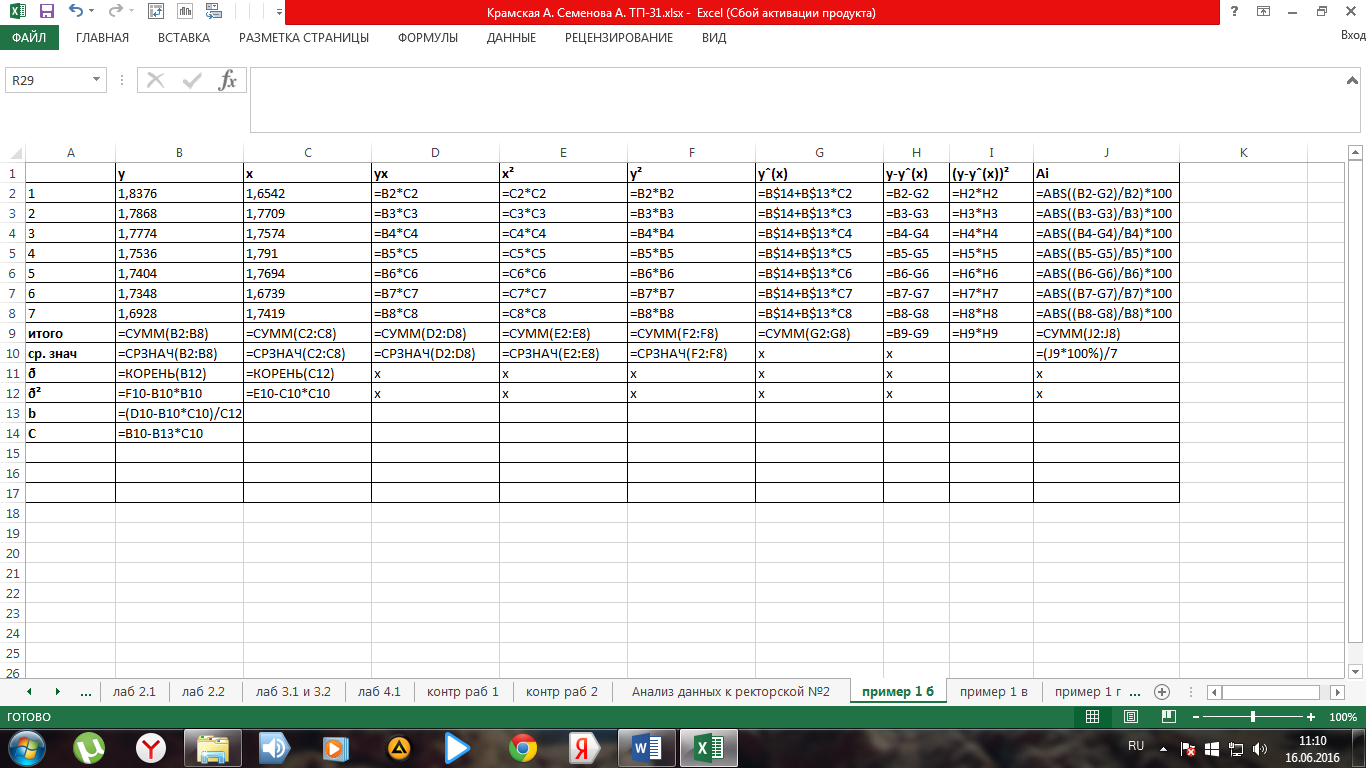
Рис. 3. Фрагмент листа электронной таблицы Microsoft Excel с расчетными формулами примера 1б
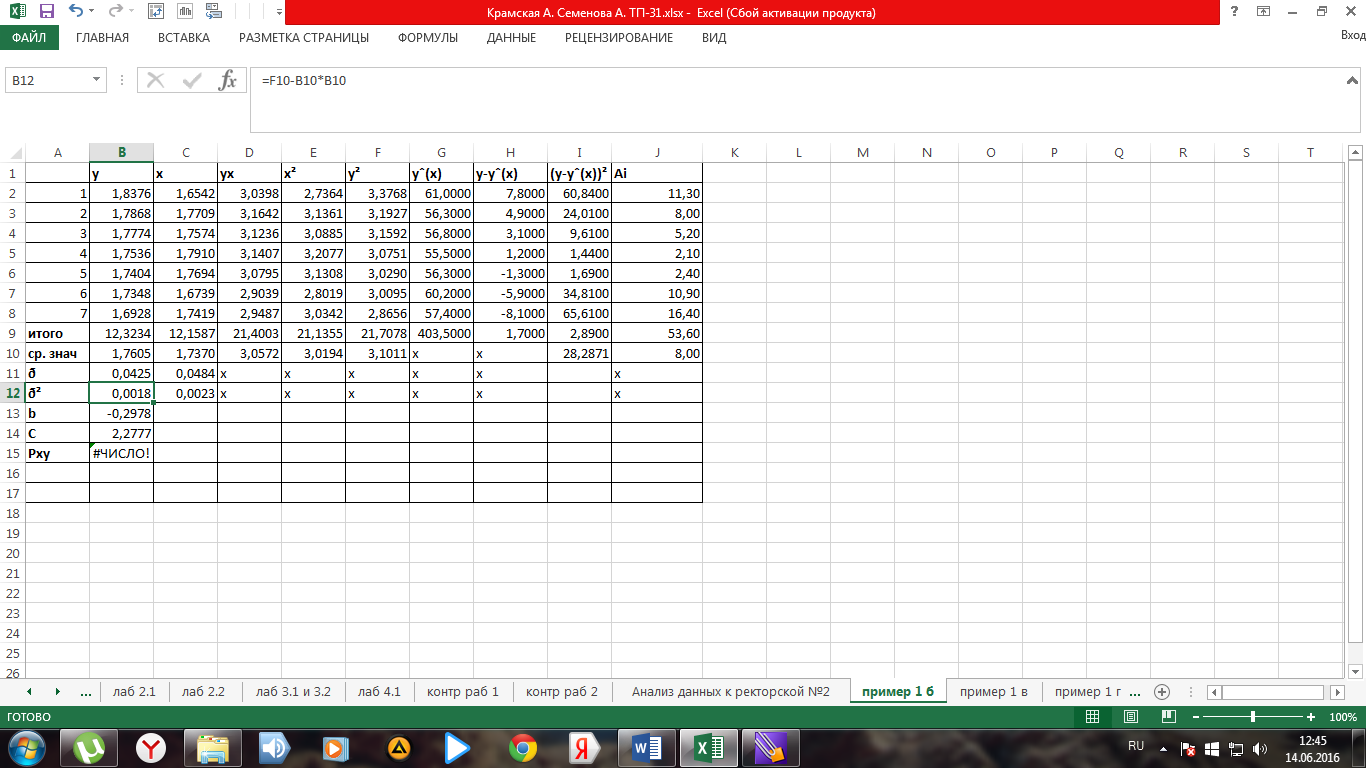
Рис. 4. Фрагмент листа электронной таблицы Microsoft Excel с решением примера 1б
Рассчитаем C и b:
b = 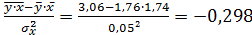 ,
,
C = y̅ - b∙x̅ =1,7605+0,298∙1,7170= 2,278.
Получим линейное уравнение: Y = 2,278 -0,298∙X.
Выполнив его потенцирование, получим:
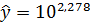 ∙
∙ 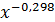 = 189,7∙
= 189,7∙ 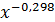
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 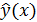 . По ним рассчитаем показатели: тесноты связи - индекс корреляции ρху и среднюю ошибку аппроксимации
. По ним рассчитаем показатели: тесноты связи - индекс корреляции ρху и среднюю ошибку аппроксимации 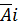 :
:
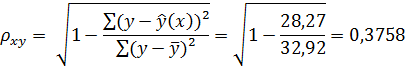
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 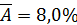
Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь.
1в. Построению уравнения показательной кривой у= 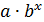 предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
lg y = lg a + x ∙lg b
Y = С +В∙х,
где Y = lg y, С = lg а, В = lg b.
Расчет представлен на рисунке 5 и 6.
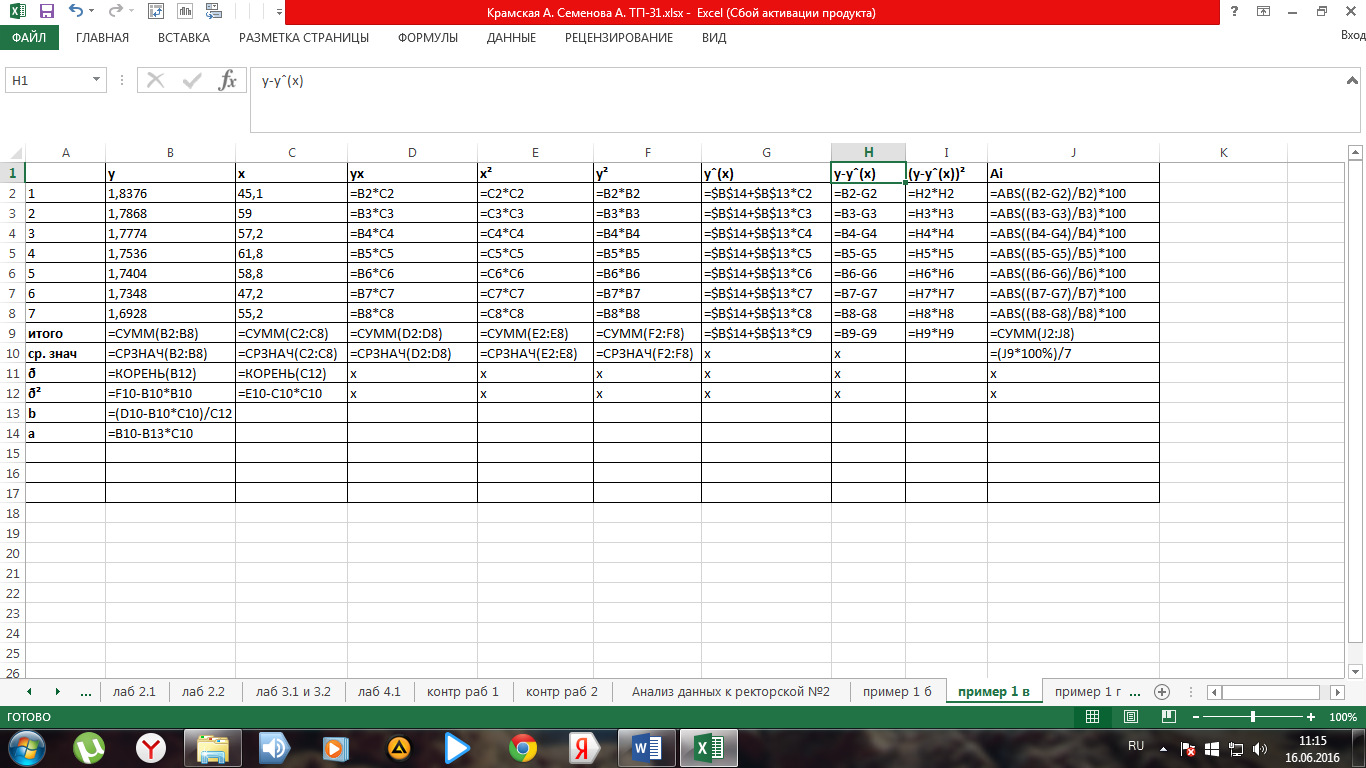
Рис. 5. Фрагмент листа электронной таблицы Microsoft Excel с расчетными формулами примера 1в
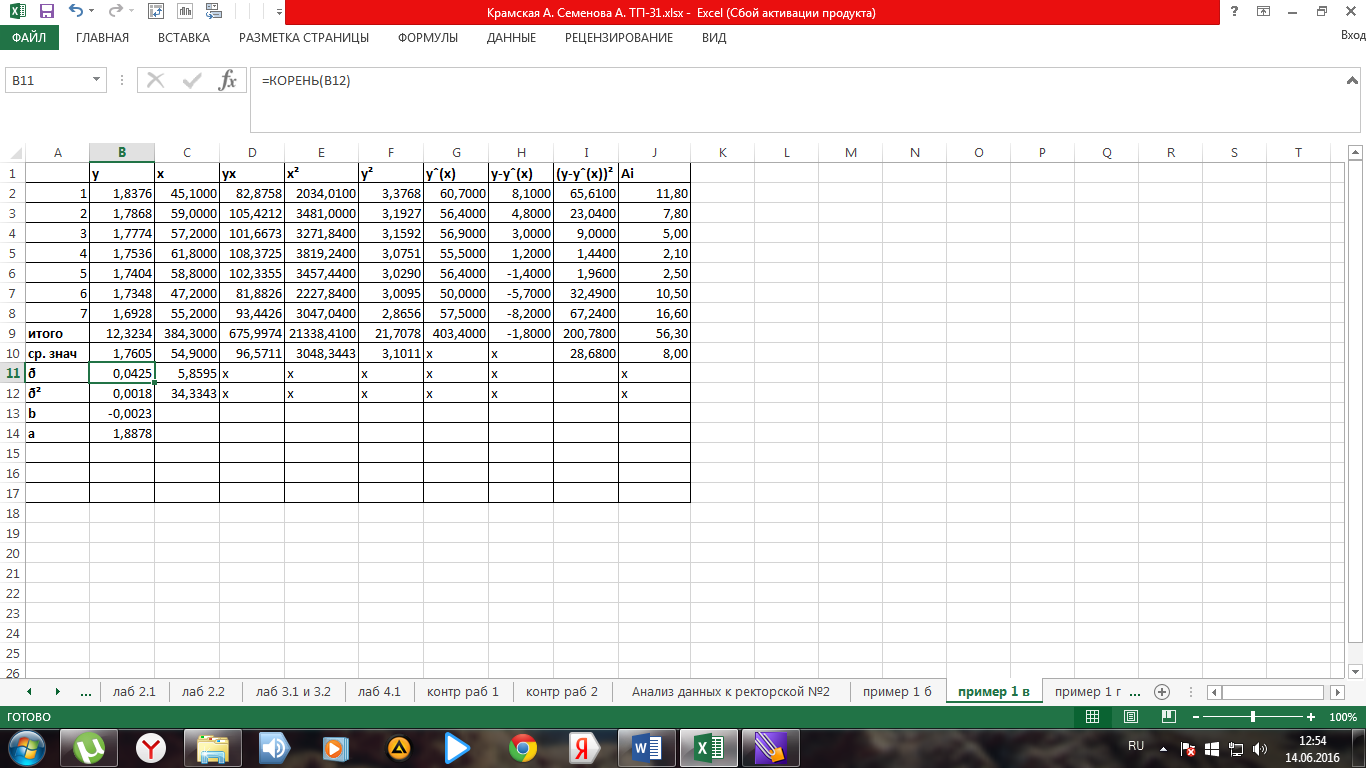
Рис. 6. Фрагмент листа электронной таблицы Microsoft Excel с решением примера 1в
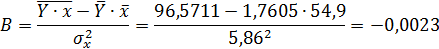
A= 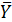 -B∙
-B∙ 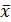 = 1,7605+0,0023∙54,9=1,887.
= 1,7605+0,0023∙54,9=1,887.
Получено линейное уравнение: 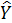 =1,887-0,0023∙x.
=1,887-0,0023∙x.
Произведем потенцирование полученного уравнения и запишем его в обычной форме:
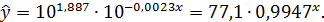
Тесноту связи оценим через индекс корреляции ρху:
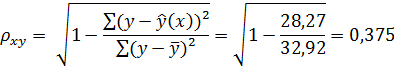
Связь умеренная. А = 8,0%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, она описывает изучаемую зависимость.
1г.Уравнение равносторонней гиперболы 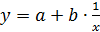 линеаризуется при замене:
линеаризуется при замене: 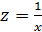 . Тогда
. Тогда 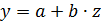 . Для расчетов используем данные рис. 7 и 8.
. Для расчетов используем данные рис. 7 и 8.
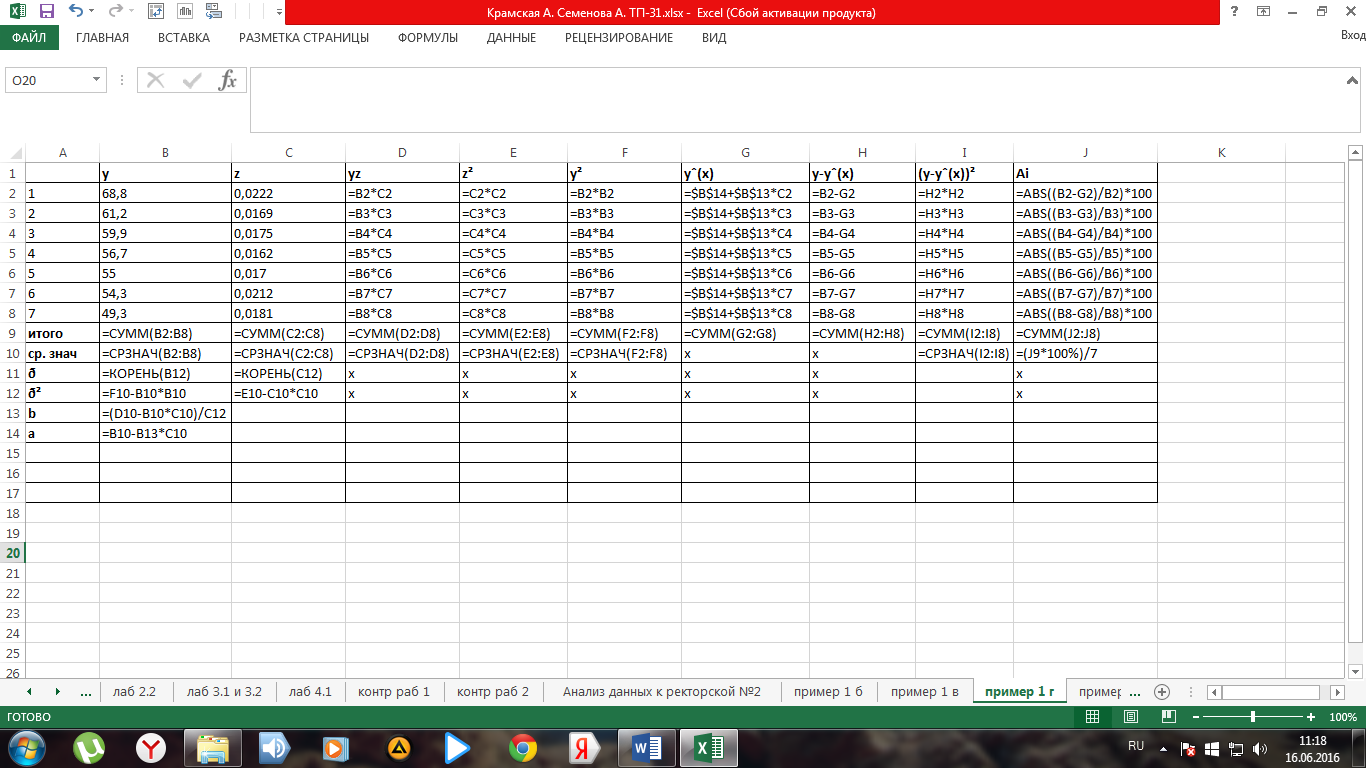
Рис. 7. Фрагмент листа электронной таблицы Microsoft Excel с расчетными формулами примера 1г
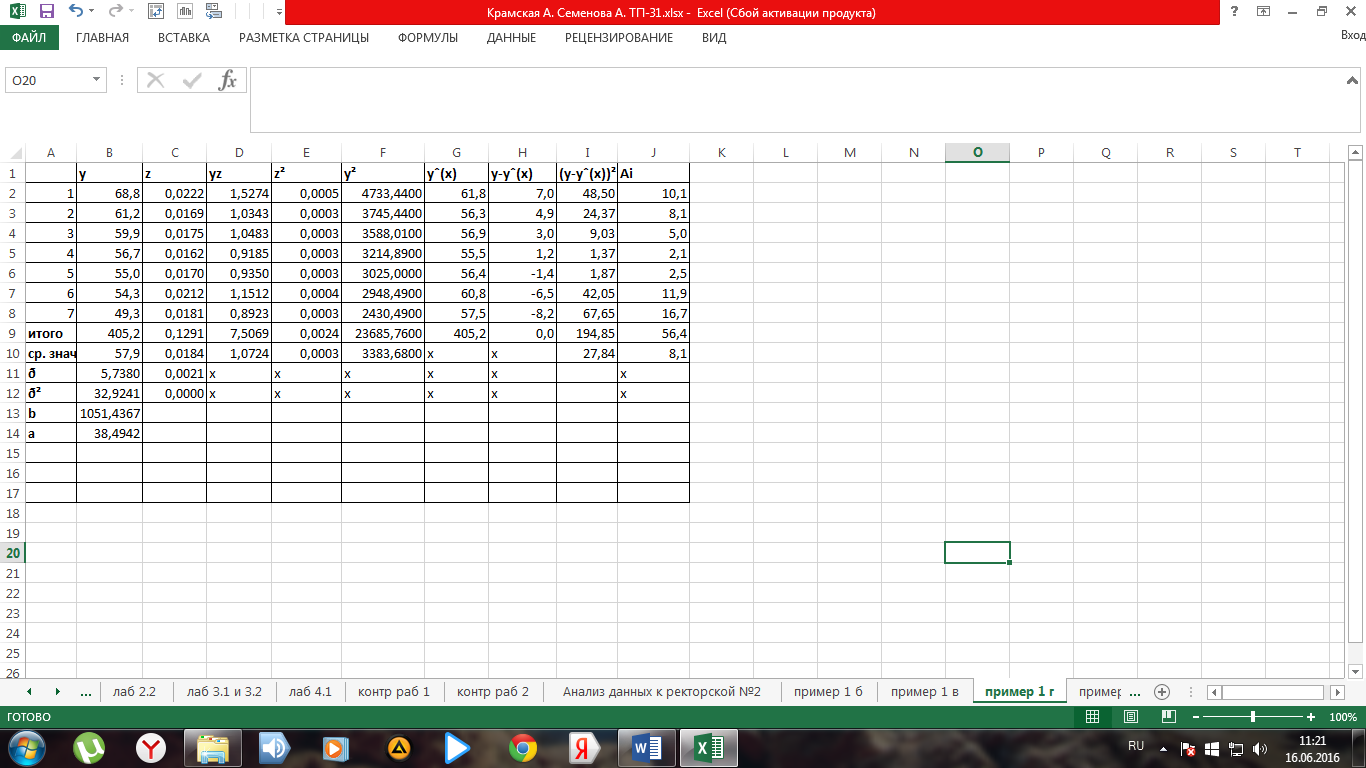 Рис. 8. Фрагмент листа электронной таблицы Microsoft Excel с решением примера 1г
Рис. 8. Фрагмент листа электронной таблицы Microsoft Excel с решением примера 1г
Значение параметров регрессии a и b составили:
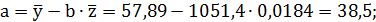
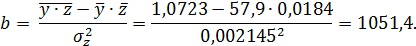
Получено уравнение: 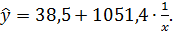
Индекс корреляции: 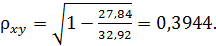
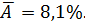 По уравнению равносторонней гиперболы получено наибольшая оценка тесноты связи:
По уравнению равносторонней гиперболы получено наибольшая оценка тесноты связи: 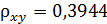 (по сравнению с линейной, степенной и показательной регрессиями).
(по сравнению с линейной, степенной и показательной регрессиями). 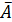 остается на допустимом уровне:
остается на допустимом уровне:
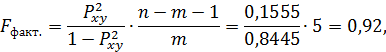
где 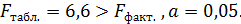
Следовательно, принимается гипотеза 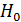 о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
Пример 2.
По территориям региона приводятся данные за 200Х г. (таблица 2).
Таблица 2
Значения признаков по территориям
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,х | Среднедневная заработная плата, руб., у |
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимумах, составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение
1. Расчет параметров уравнения линейной регрессии представлен на рисунке 9 и 10.
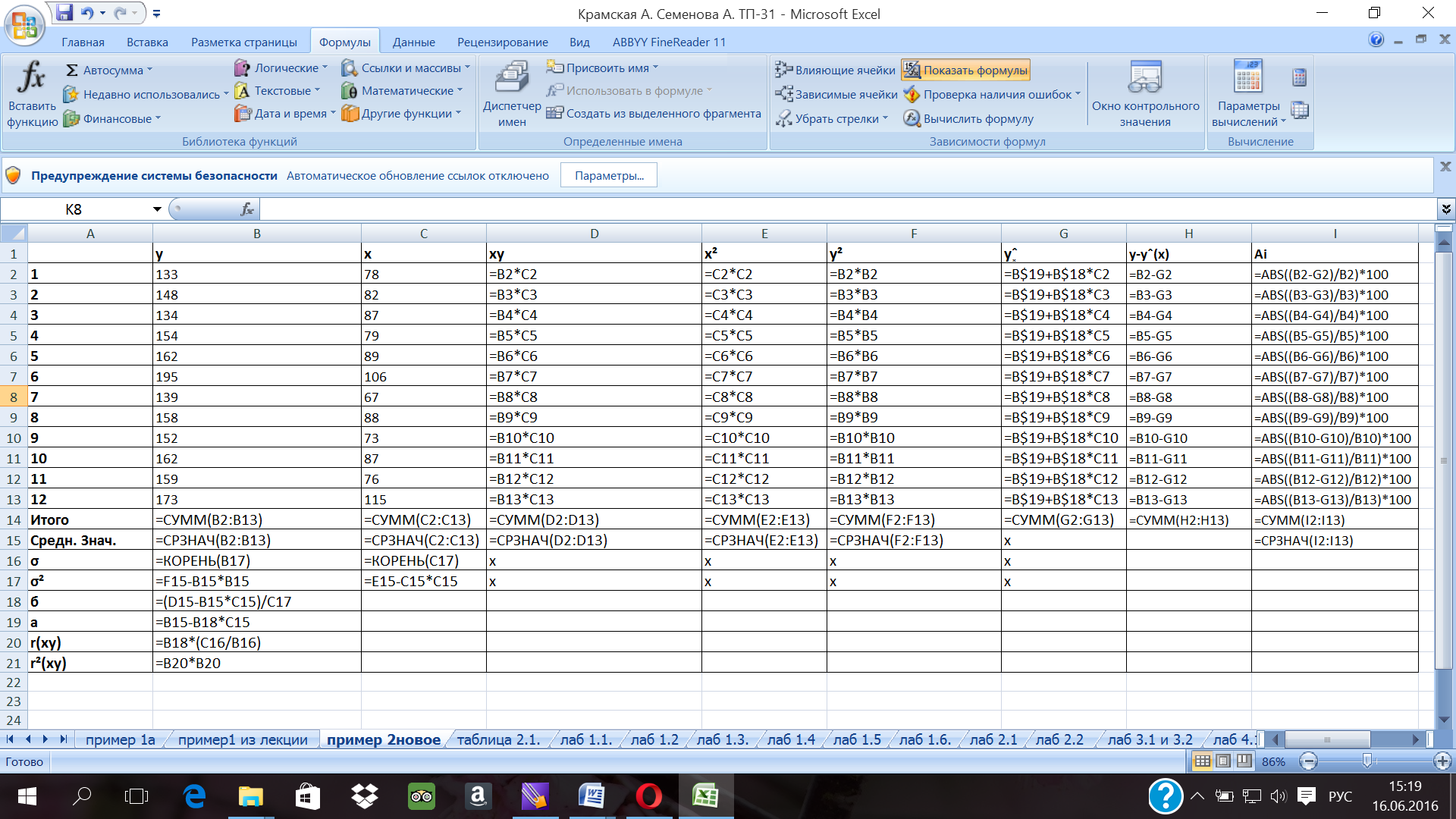
Рис. 9. Фрагмент листа электронной таблицы Microsoft Excel с расчетными формулами примера 2
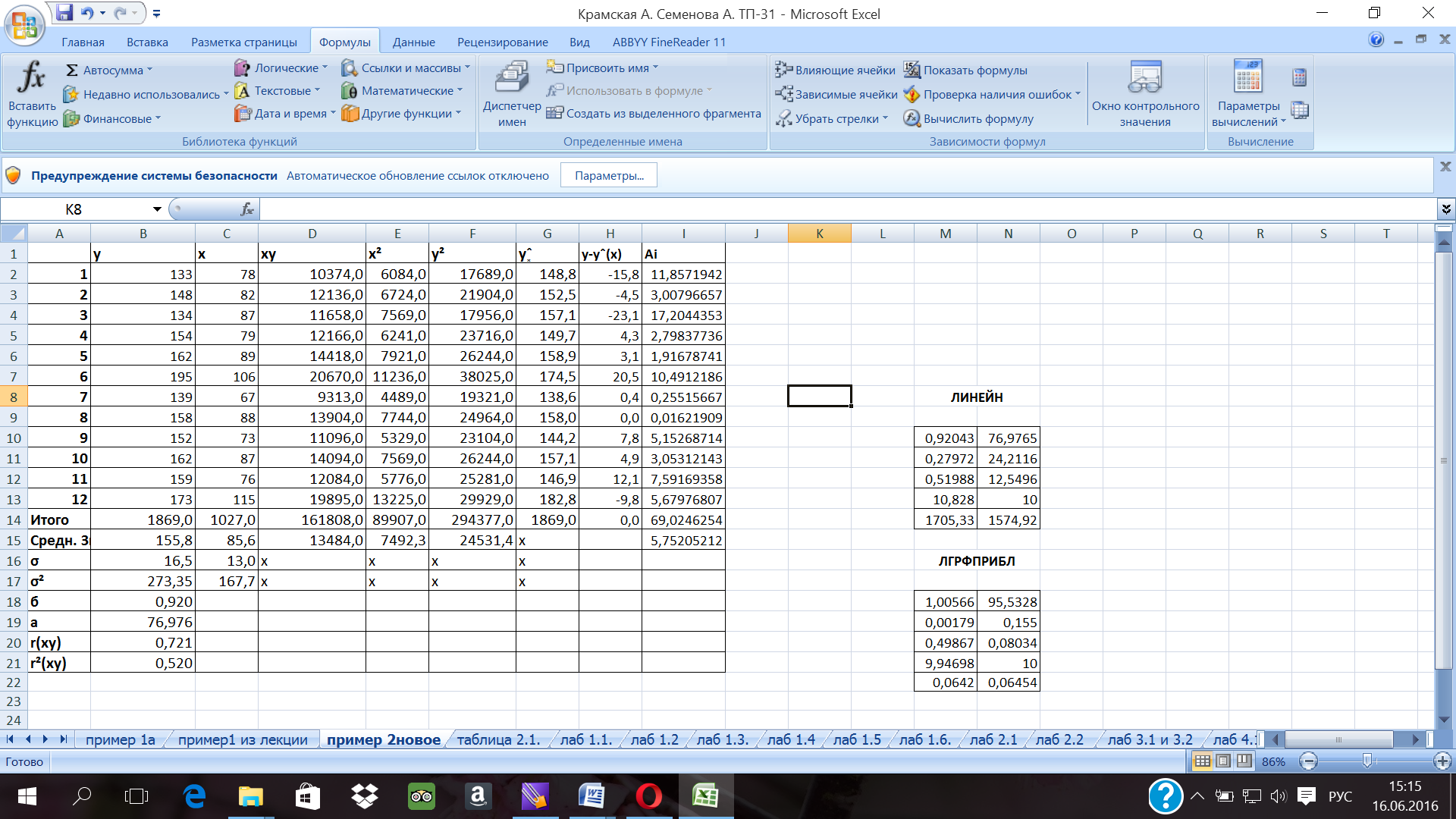
Рис.10. Фрагмент листа электронной таблицы Microsoft Excel с решением примера 2
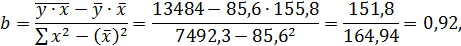
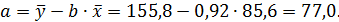
Получено уравнение регрессии: 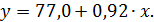
C увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
2. Тесноту линейной связи оценит коэффициент корреляции:
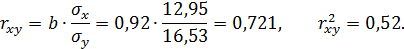
Это означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х - среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации:
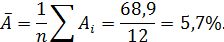
Качество построенной модели оценивается как хорошее, так как 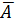 не превышает 8 - 10%.
не превышает 8 - 10%.
3. Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля: 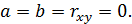
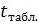 для числа степеней свободы
для числа степеней свободы 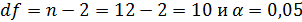 составит 2,23.
составит 2,23.
Определим случайные ошибки 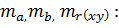

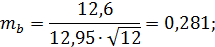
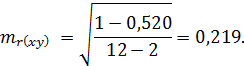
Тогда
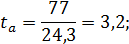
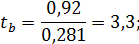
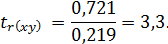
Фактические значения t-статистики превосходят табличные значения:
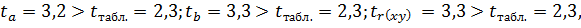 поэтому гипотеза Н0 отклоняется, т. е. a, b и
поэтому гипотеза Н0 отклоняется, т. е. a, b и 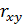 не случайно отличаются от нуля, а статистически значимы.
не случайно отличаются от нуля, а статистически значимы.
Рассчитаем доверительный интервал для a и b. Для этого определим предельную ошибку для каждого показателя:
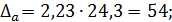
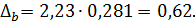
Доверительные интервалы:
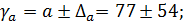
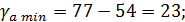
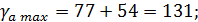
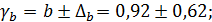
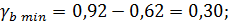
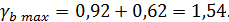
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью р = 1- 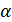 = 0,95 параметры a и b, находясь в указанных границах, не принимают нулевых значений, т. е. не являются статистически незначимыми и существенно отличны от нуля.
= 0,95 параметры a и b, находясь в указанных границах, не принимают нулевых значений, т. е. не являются статистически незначимыми и существенно отличны от нуля.
4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: 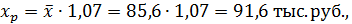 тогда прогнозное значение прожиточного минимума составит:
тогда прогнозное значение прожиточного минимума составит:
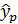 = 77 + 0,92 ∙ 91,6 = 161 тыс. руб.
= 77 + 0,92 ∙ 91,6 = 161 тыс. руб.
5. Ошибка прогноза составит:
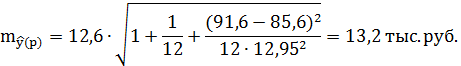
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:
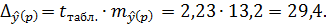
Доверительный интервал прогноза:
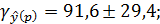
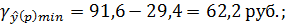
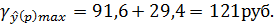
Выполненный прогноз среднемесячной заработной платы оказался надежным (р = 1 - 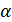 = 1 - 0,05 = 0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала
= 1 - 0,05 = 0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала 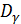 составляет 1,95 раза:
составляет 1,95 раза:
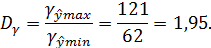
Пример 3.
По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции у от факторов, приведенных в таблице 3.
Таблица 3
Зависимость себестоимость единицы продукции у от факторов.
| Признак-фактор | Уравнение парной регрессии | Среднее значение фактора |
| Объем производства, млн. руб., x1 | 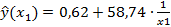
| 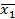 =2,64 =2,64
|
| Трудоемкость единицы прод., чел./час, x2 | 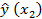 = 9,30+9,83∙ = 9,30+9,83∙ 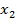
| 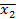 = 1,38 = 1,38
|
| Оптовая цена за 1 т энергоносителя, млн руб., x3 | 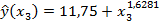
| 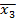 = 1,503 = 1,503
|
| Доля прибыли, изымаемой государством, %, x4 | 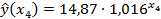
| 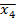 = 26,3 = 26,3
|
1) Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат;
2) Ранжировать факторы по силе влияния.
Решение
1. Для уравнения равносторонней гиперболы
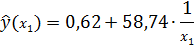
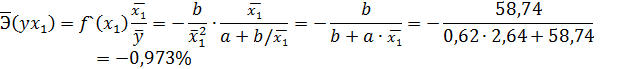
Для уравнения прямой 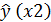 = 9,30+9,83∙
= 9,30+9,83∙ 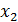 :
:
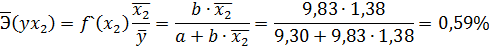
Для уравнения степенной зависимости
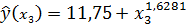
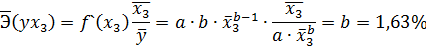
Для уравнения показательной зависимости
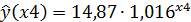
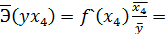 a∙
a∙ 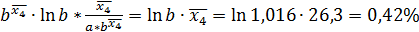
2. Сравнивая значения 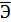 ухi, ранжируем хj по силе их влияния на себестоимость единицы продукции:
ухi, ранжируем хj по силе их влияния на себестоимость единицы продукции:
а) 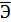 ух3 = 1,63% ; в)
ух3 = 1,63% ; в) 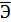 уx2 = 0,59% ;
уx2 = 0,59% ;
б) 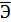 yx1= -0,973% ; г)
yx1= -0,973% ; г) 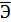 уx4 = 0,42% .
уx4 = 0,42% .
Для формирования уровня себестоимости продукции группы предприятий первоочередное значение имеют цены на энергоносители; в гораздо меньшей степени влияют трудоемкость продукции и отчисляемая часть прибыли. Фактором снижения себестоимости выступает размер производства: с ростом его на 1% себестоимость единицы продукции снижается на -0,97%.
Пример 4.
Зависимость потребления продукта А от среднедушевого дохода по данным 20 семей характеризуется следующим образом: уравнение регрессии 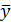 х = 2 ∙
х = 2 ∙ 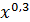 ; индекс корреляции ρху = 0,9; остаточная дисперсия
; индекс корреляции ρху = 0,9; остаточная дисперсия 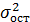 = 0,06.
= 0,06.
Провести дисперсионный анализ полученных результатов. Решение
Результаты дисперсионного анализа приведены в таблица 4.
Таблица 4
Результаты дисперсионного анализа
| Вариация результата y | Число степеней свободы | Сумма квадратов отклонений, S | Дисперсия на одну степень свободы, D | Fфакт | Fтабл а = 0,05, k1 =1, k2 = 18 |
| Общая | df=n-1 = 19 | 6,316 | - | - | - |
| Факторная | k1 = m= 1 | 5,116 | 5,116 | 76,7 | 4,41 |
| Остаточная | k2 =п-т - 1 = 18 | 1,200 | 0,0667 | - | - |
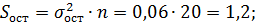
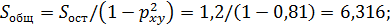
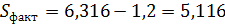
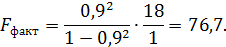
В силу того, что Fфакт = 76,7 > Fтабл = 4,4, гипотеза о случайности различий факторной и остаточной дисперсий отклоняется. Эти различия существенны, статистически значимы, уравнение надежно, значимо, показатель тесноты связи надежен и отражает устойчивую зависимость потребления продукта А от среднедушевого дохода.
Реализация типовых задач на компьютере с помощью ППП Excel
1. Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии у = а + b ∙ х.
Порядок вычисления следующий:
1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
2) выделите область пустых ячеек 5x2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1x2 - для получения только оценок коэффициентов регрессии;
3) активизируйте Мастер функций любым из способов:
а)в главном меню выберитеВставка/Функция;
б)на панели инструментовСтандартная щелкните по кнопке Вставка функции;
4) в окне Категория (рис.11) выберитеСтатистические, в окне Функция -ЛИНЕЙН. Щелкните по кнопкеОК;
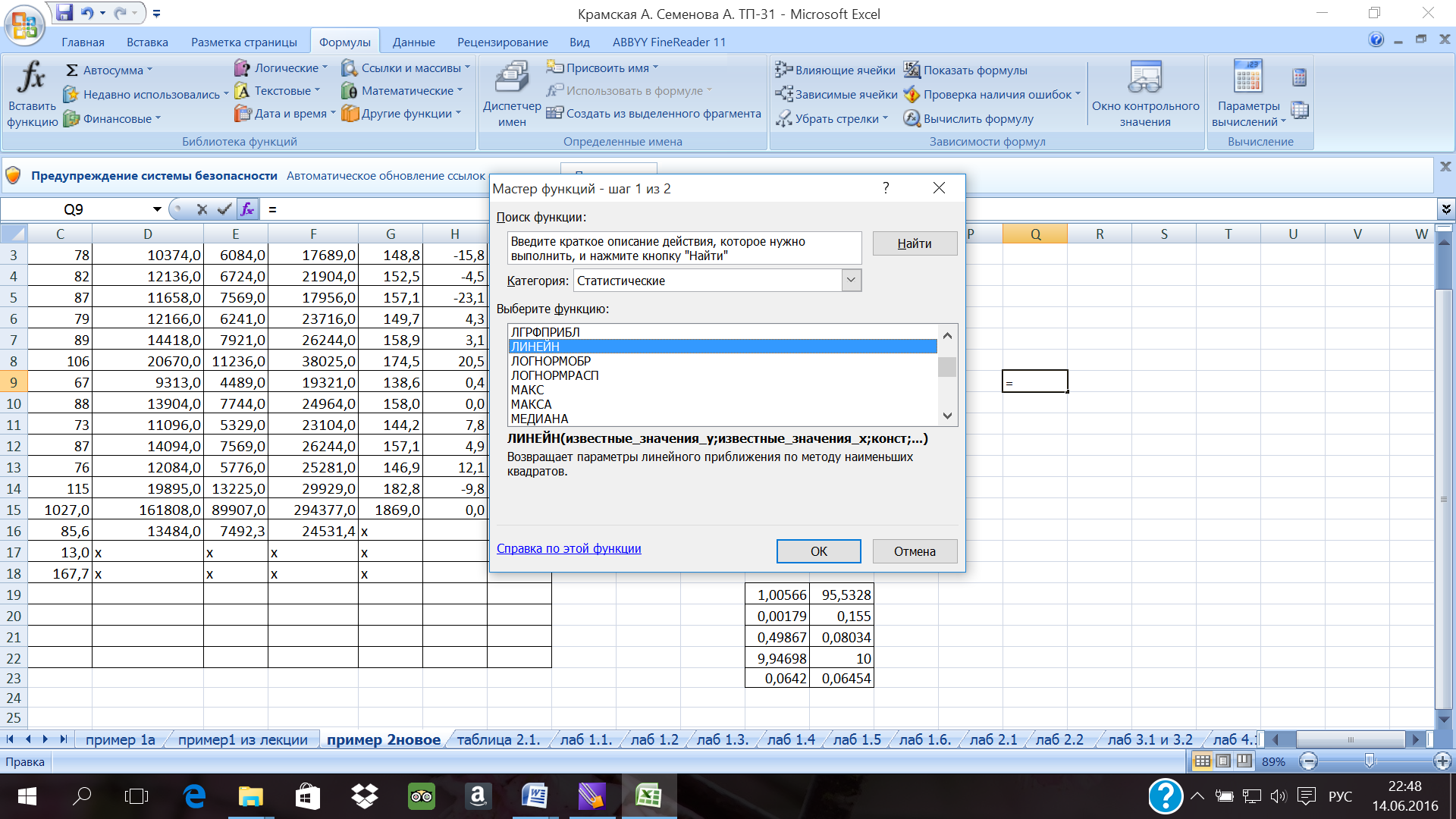
Рис. 11. Диалоговое окно «Мастер функций»
5) заполните аргументы функции (рис. 12):
Известные_значения_у - диапазон, содержащий данные результативного признака;
Известные_значения_х - диапазон, содержащий данные факторов независимого признака;
Константа - логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0; Статистика - логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика - 0, то выводятся только оценки параметров уравнения. Щелкните по кнопке ОК;
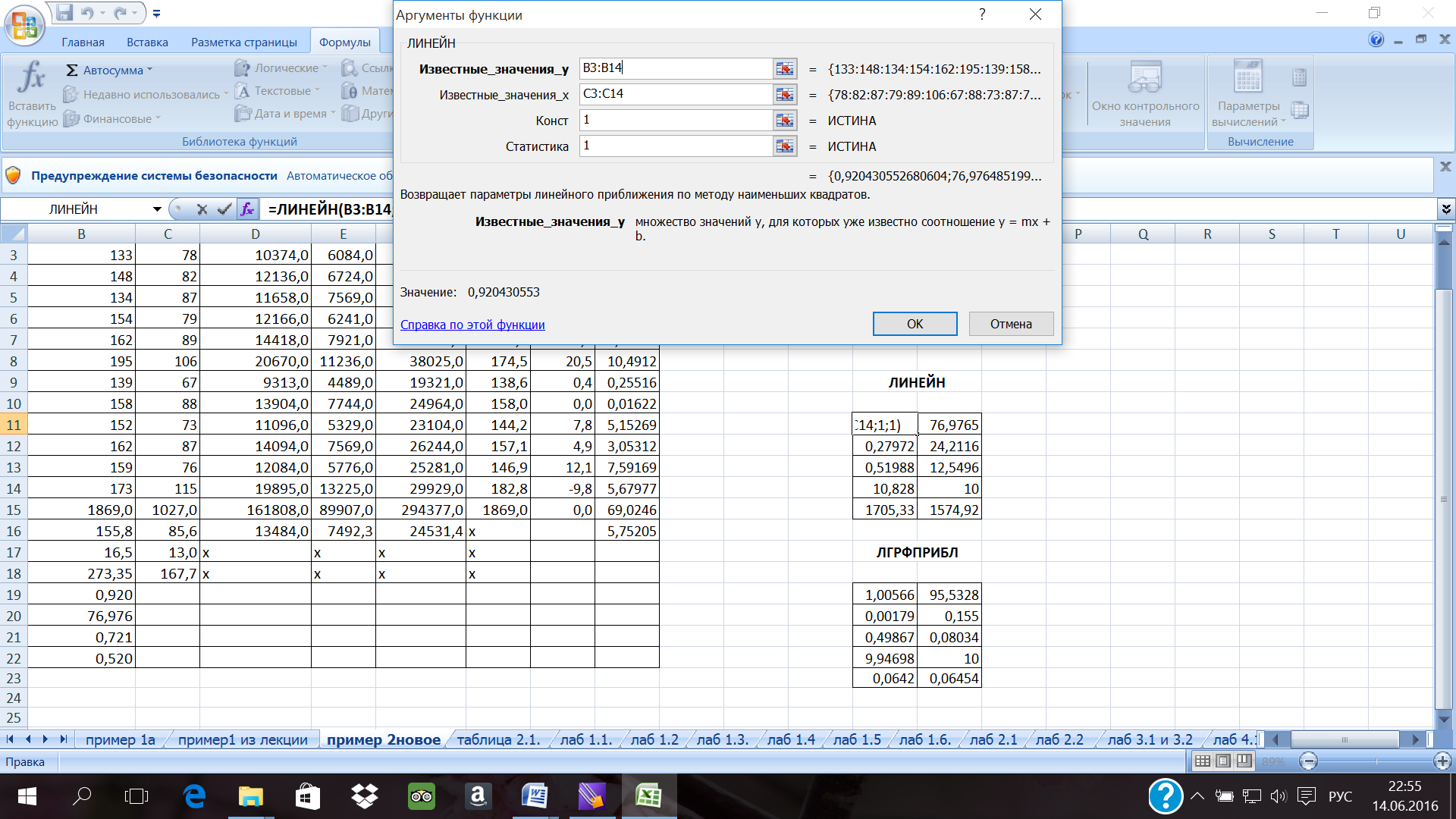
Рис. 12. Диалоговое окно ввода аргументов функции ЛИНЕЙН
6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем - на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме (таб. 5).
Таблица 5
Регрессионная статистика
| Значение коэффициента b | Значение коэффициента а |
| Среднеквадратическое отклонение b | Среднеквадратическое отклонение а |
| Коэффициент детерминации R2 | Среднеквадратическое отклонение у |
| F-статистика | Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
Для вычисления параметров экспоненциальной кривой 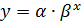 в MS Excel применяется встроенная статистическая функцияЛГРФПРИБЛ. Порядок вычисления аналогичен применению функцииЛИНЕЙН.
в MS Excel применяется встроенная статистическая функцияЛГРФПРИБЛ. Порядок вычисления аналогичен применению функцииЛИНЕЙН.
Для данных из примера 2 результат вычисления функции ЛИНЕЙН представлен на рис. 13, функцииЛГРФПРИБЛ - на рис. 14.
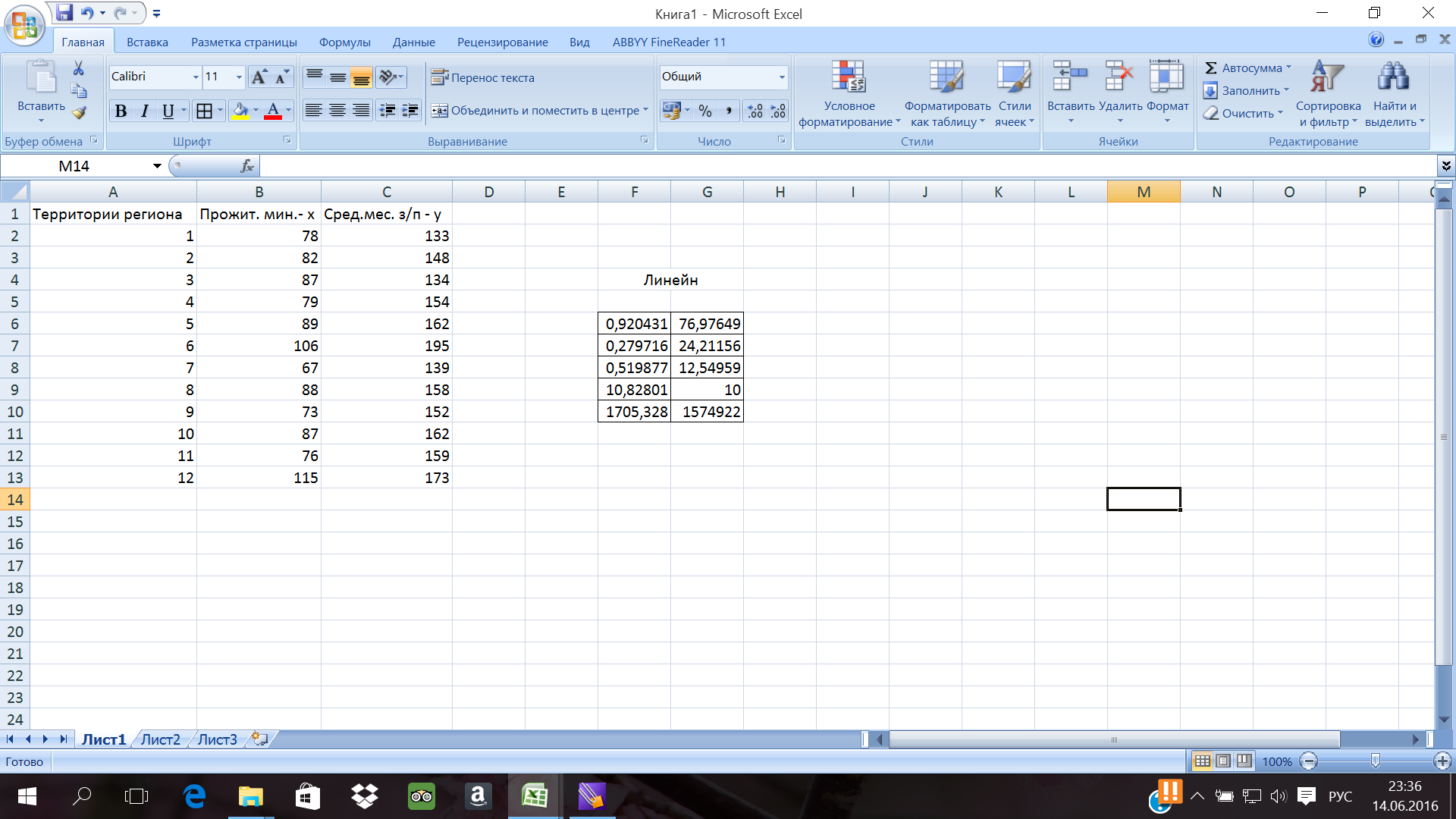
Рис. 13. Результат вычисления функции ЛИНЕЙН
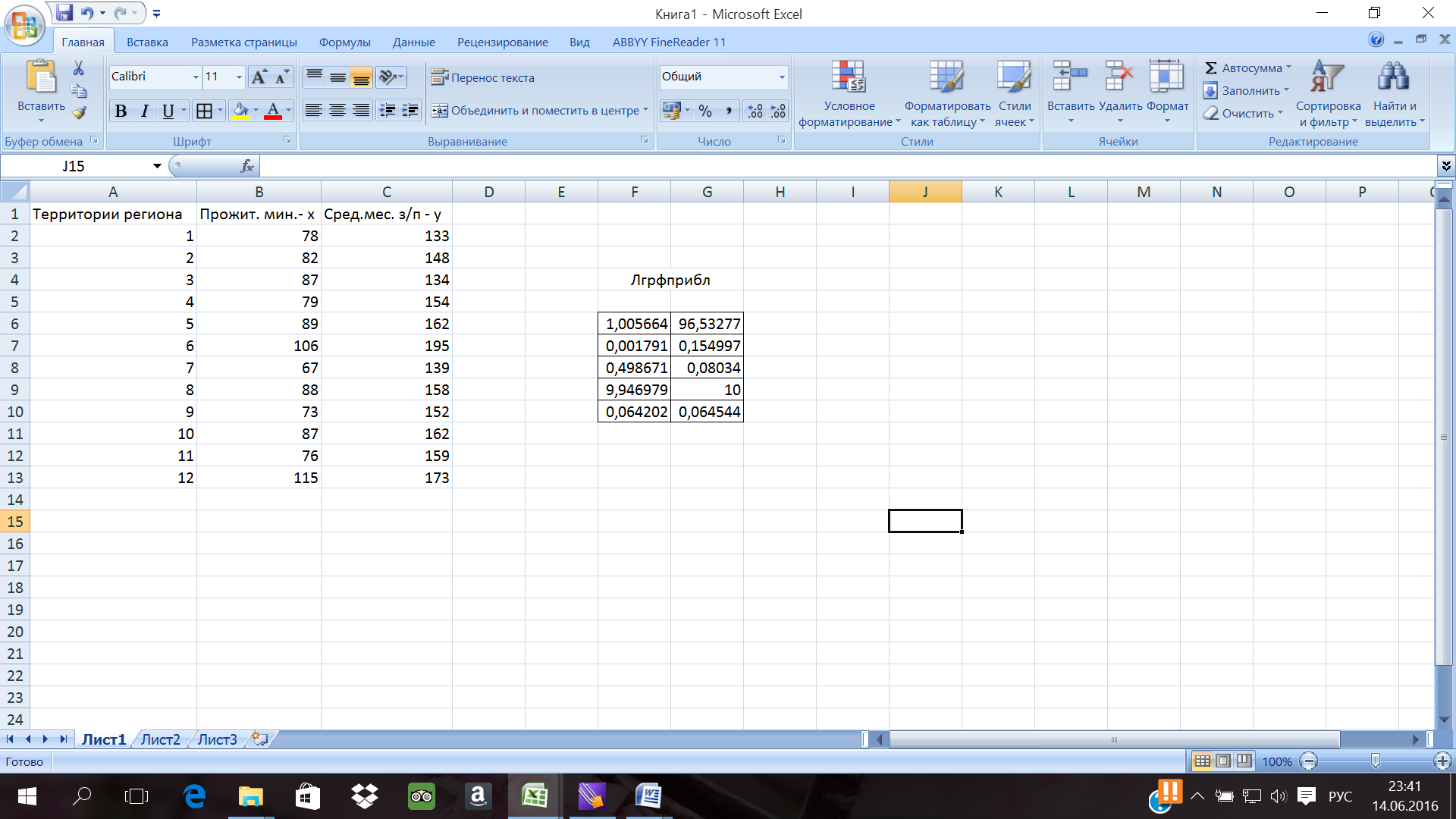
Рис. 14. Результат вычисления функции ЛГРФПРИБЛ
2. С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности Порядок действий следующий.
1) проверьте доступ к пакету анализа В главном меню последовательно выберите Сервис /Надстройки. Установите флажок Пакет анализа (рис. 15);
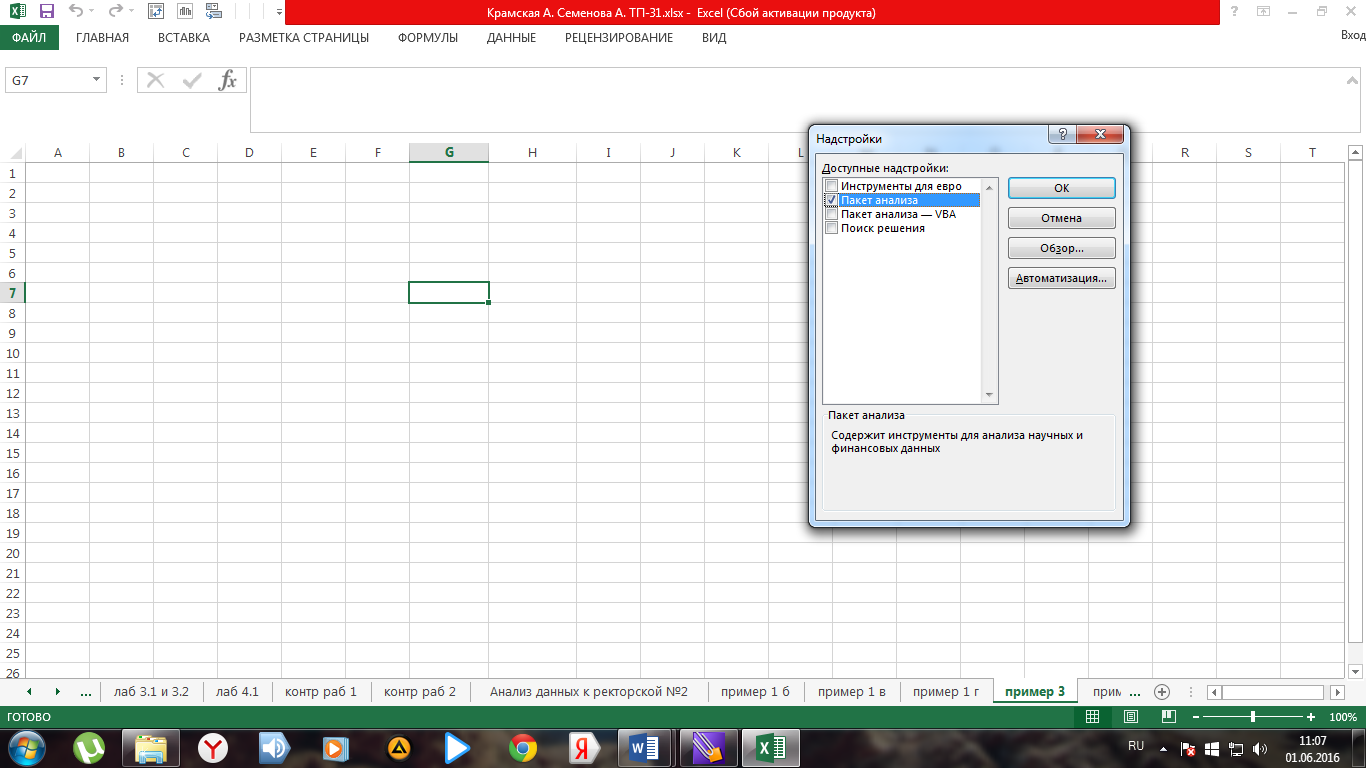
Рис.15. Подключение надстройки Пакет анализа
2) в главном меню выберите Сервис/Анализ данных/Регрессия.
Щелкните по кнопке ОК;
3) заполните диалоговое окно ввода данных и параметров вывода (рис.16)
Входной интервал Y - диапазон, содержащий данные результативного признака,
Входной интервал X - диапазон, содержащий данные факторов независимого признака;
Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа - ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист - можно задать произвольное имя нового листа.
Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.
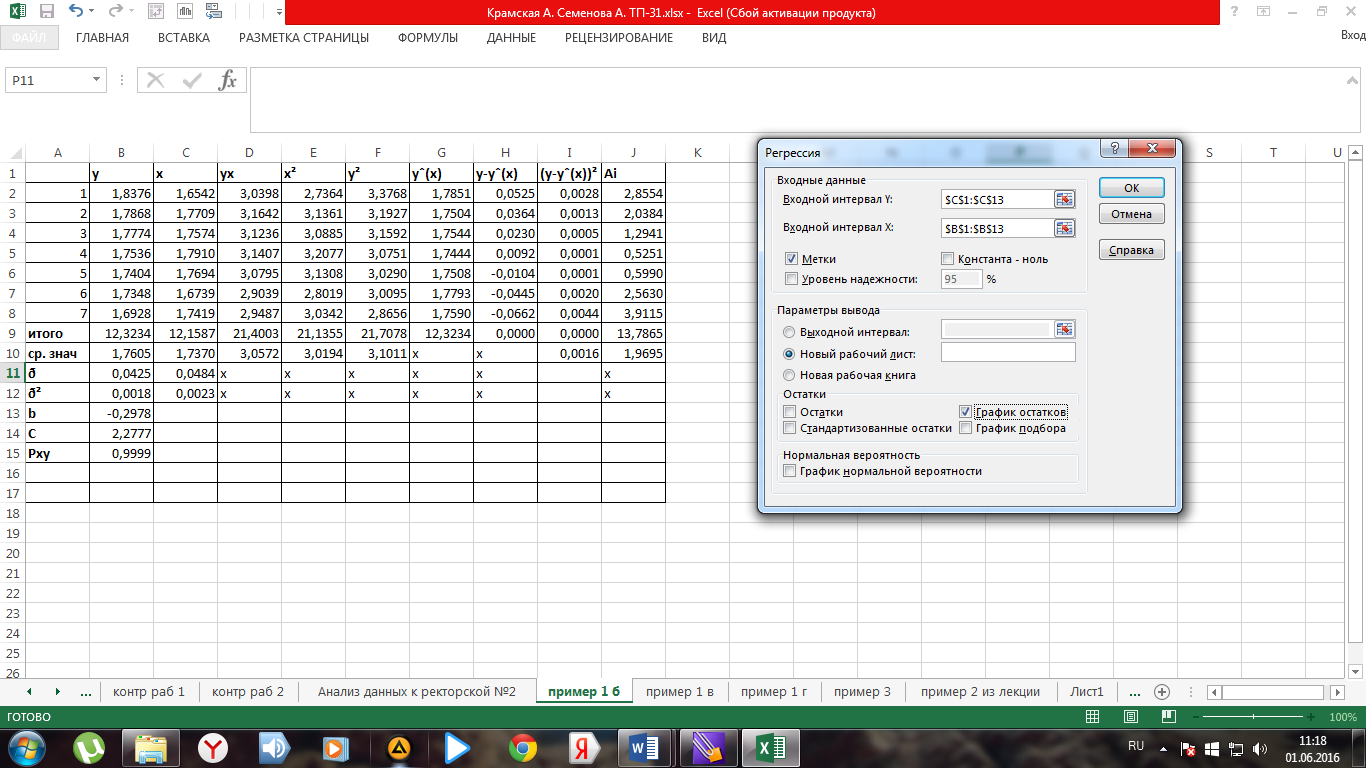
Рис. 16. Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных из примера 2 представлены на рис. 17.
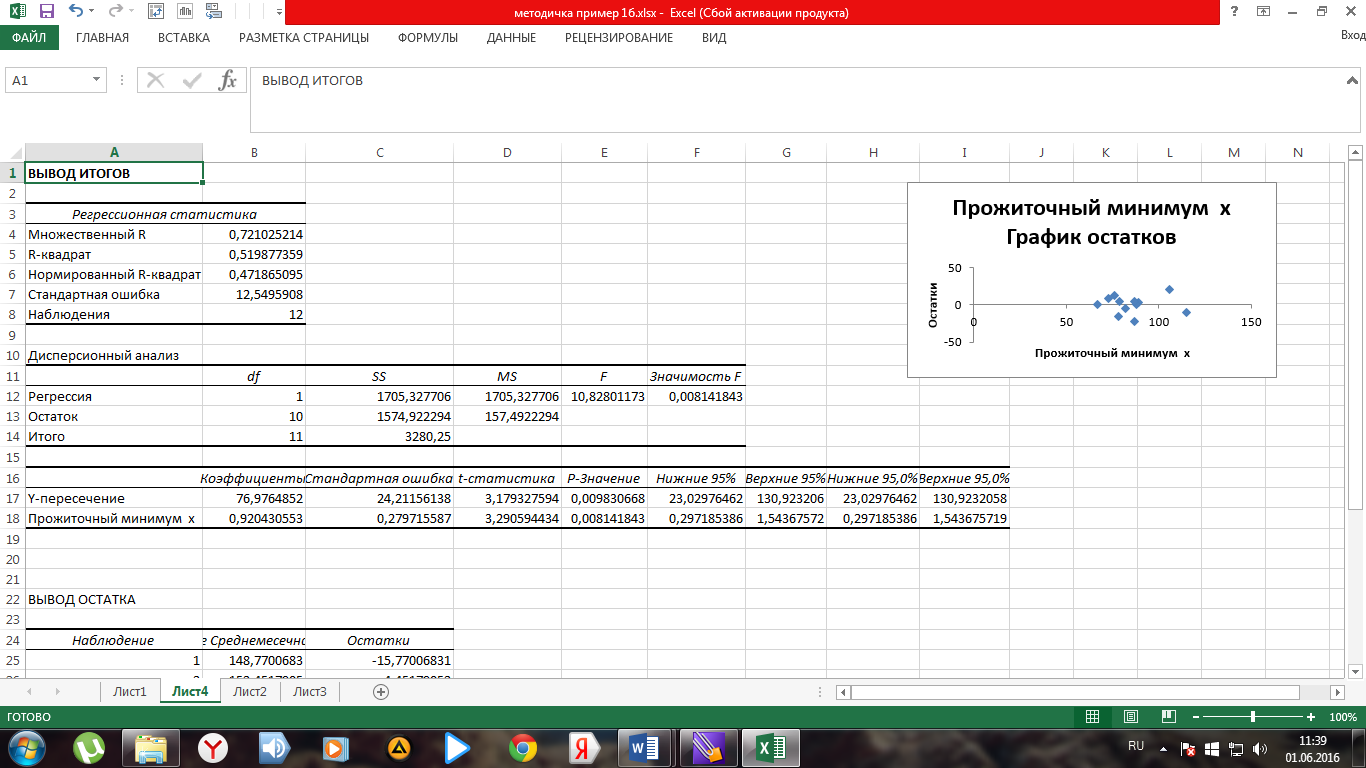
Рис. 17. Результат применения инструмента Регрессия
Задание 1.
Выполнить по вариантам контрольные задания 1-26, представленные в Приложении 1.
|
из
5.00
|
Обсуждение в статье: Реализация типовых задач на компьютере с помощью ППП Excel |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

