 |
Главная |
Квантовые числа. Принцип Паули.
|
из
5.00
|
Представление Бора об определенных орбитах, по которым движутся электроны в атоме, оказалось весьма условным. На самом деле движение электрона в атоме очень мало похоже на движение планет или спутников. Физический смысл имеет только вероятность обнаружить электрон в том или ином месте, описываемая квадратом модуля волновой функции |Ψ|2. Оказалось, что состояние электрона в атоме характеризуется целым набором квантовых чисел:
1) главное квантовое числоn - определяет энергию и орбиту электрона (n = 1,2,3…).
2) орбитальное квантовое число l – определяет форму орбиты и момент импульса:
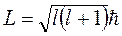 ,
,  = 0, 1, 2… (n – 1)
= 0, 1, 2… (n – 1)
3) магнитное квантовое числоm – определяет проекцию орбитального момента импульса электрона на некоторое произвольно выбранное направление z внешнего магнитного поля. Для каждого значения  вектор
вектор  ориентируется только так, чтобы его проекция
ориентируется только так, чтобы его проекция 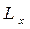 была равна
была равна
 ,
,
При данном значении  магнитное квантовое число принимает значения: 0, ±1, ±2,…. ±
магнитное квантовое число принимает значения: 0, ±1, ±2,…. ±  , т.е. всего (2l + 1) значений.
, т.е. всего (2l + 1) значений.
Таким образом, каждое квантовое состояние электрона в атоме характеризуется набором целых чисел – n , l , m – квантовых чисел.
4) электрон имеет собственную характеристику, связанную с вращением электрона вокруг собственной оси – спин (S) (от англ. spin – вращать)– собственный механический и магнитный момент. Для электронов спиновое квантовое число принимает всего два значения
 .
.
Собственный момент импульса электрона определяется через спиновое квантовое число по формуле:
LS = ћ 
Опытным путем было установлено, что отношение собственного магнитного и механического моментов электрона равно:
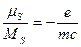 ,
,
где µS = собственный магнитный момент электрона; m – масса электрона; е - заряд электрона.
Спином обладают все элементарные частицы. По величине спина элементарные частицы делятся на фермионы и бозоны.
Частицы, обладающие нулевым или целым спином называются бозонами (фотон, α – частица), подчиняются статистике Бозе – Эйнштейна, описываются симметричной волновой функцией, не подчиняются принципу Паули.
Частицы, обладающие полуцелым спином называются фермионами (электроны), подчиняются статистике Ферми – Дирака, описываются антисимметричной волновой функцией, подчиняются принципу Паули.
Принцип Паули гласит: в одном и том же атоме не может быть двух (и более) электронов с четырьмя одинаковыми квантовыми числами.
Или: не существует даже 2 фермионов, находящихся в одном квантовом состоянии.
Максимальное число электронов, находящихся в состояниях, определяемых данным квантовым числом равно:
Z(n) = 
Рентгеновские спектры
Рентгеновские спектры – это спектры испускания и поглощения рентгеновского излучения (10-9 до 10-12м).
 Рентгеновские спектры состоят из нескольких серий, обозначаемых К, L , M , N и О. Каждая серия содержит небольшой набор отдельных линий, обозначенных в порядке убывания λ индексами: α, β, γ и т.д.
Рентгеновские спектры состоят из нескольких серий, обозначаемых К, L , M , N и О. Каждая серия содержит небольшой набор отдельных линий, обозначенных в порядке убывания λ индексами: α, β, γ и т.д.
Механизм возникновения рентгеновских спектров следующий: под влиянием внешнего электрона или высокоэнергетического фотона вырывается один из двух электронов К оболочки атома. Тогда на его место может перейти электрон с более удаленных от ядра оболочек L , M , N… Такие переходы сопровождаются испусканием рентгеновских квантов и возникновению спектральных линий К – серии. Самой длинноволновой линией К – серии является Кα – линия. К – серия сопровождается обязательно другими сериями, т.к. появляются вакансии в оболочках L , M , N…
Эти спектры исследовал англ. физик Мозли и установил, что частоты возрастают с увеличением порядкового номера:
ν = R(Z-σ)2 (  )
)
R – постоянная Ридберга;
ν – частота, соответствующая данной линии рентгеновского излучения;
m = 1, 2, 3 – определяет рентгеновскую серию;
n = m +1,… - определяет отдельную линию серии;
σ – постоянная экранирования.
Смысл постоянной экранирования заключается в том, что на электрон, совершающий переход, действует не весь заряд ядра Ze, а заряд е(Z – σ), ослабленный экранирующим действием других электронов. Например, для Кα – линии σ = 1 и закон Мозли будет иметь вид:
ν = R(Z – 1)2 ( 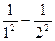 )
)
|
из
5.00
|
Обсуждение в статье: Квантовые числа. Принцип Паули. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

