 |
Главная |
Лабораторная работа № 4. Нелинейная парная регрессия
|
из
5.00
|
Цель работы. Освоение способов перехода от нелинейной взаимосвязи зависимой и объясняющей переменной к линейной модели; освоение построения по выборочным данным нелинейной модели парной регрессии; оценка значимости построенной модели и ее прогностических свойств; оценка точности и надежности параметров модели; построение прогнозов значений зависимой переменной в MS Excel 2010. Интерпретация модели.
Краткие сведения. В парной линейной регрессии взаимосвязь наблюдаемых в выборке значений  зависимой переменной
зависимой переменной  и значений
и значений  фактора X описывается линейной по
фактора X описывается линейной по  и линейной по параметрам зависимостью
и линейной по параметрам зависимостью  . Она не всегда наилучшим образом отражает существующую взаимосвязь
. Она не всегда наилучшим образом отражает существующую взаимосвязь  и X. Поэтому наряду с парной линейной регрессией рассматривают и нелинейные модели парной регрессии, в которых исследуются нелинейные взаимосвязи
и X. Поэтому наряду с парной линейной регрессией рассматривают и нелинейные модели парной регрессии, в которых исследуются нелинейные взаимосвязи  и
и  .
.
Различают два класса нелинейных моделей регрессии:
· регрессии, нелинейные относительно объясняющих переменных, но линейные относительно параметров модели, например,  ,
, 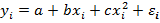 или
или 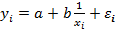 ;
;
· регрессии нелинейные по параметрам, например,  или
или  .
.
1. Нелинейные по объясняющим переменным, но линейные по параметрам, уравнения регрессии введением новых объясняющих переменных сводятся к линейным регрессионным уравнениям и оцениваются методом наименьших квадратов. Например: нелинейная модель  введением новой переменной
введением новой переменной  приводится к линейной модели парной регрессии
приводится к линейной модели парной регрессии 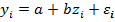 ; нелинейная модель
; нелинейная модель 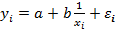 введением новой объясняющей переменной
введением новой объясняющей переменной  также приводится к линейной модели парной регрессии
также приводится к линейной модели парной регрессии 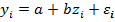 ; нелинейная модель
; нелинейная модель 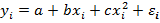 введением новой объясняющей переменной
введением новой объясняющей переменной 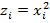 приводится к линейной модели множественной регрессии
приводится к линейной модели множественной регрессии  . Параметры нелинейных по объясняющим переменным, но линейных по параметрам, уравнений регрессии совпадают с параметрами преобразованного линейного уравнения регрессии. Ошибки регрессии
. Параметры нелинейных по объясняющим переменным, но линейных по параметрам, уравнений регрессии совпадают с параметрами преобразованного линейного уравнения регрессии. Ошибки регрессии  преобразованной линейной модели должны удовлетворять предпосылкам линейной регрессии. Оценки метода наименьших квадратов параметров преобразованной линейной модели являются оценками параметров исходной нелинейной модели. Например, для нелинейной модели
преобразованной линейной модели должны удовлетворять предпосылкам линейной регрессии. Оценки метода наименьших квадратов параметров преобразованной линейной модели являются оценками параметров исходной нелинейной модели. Например, для нелинейной модели 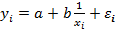 оцененным уравнением регрессии будет
оцененным уравнением регрессии будет 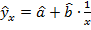 , где
, где  и
и  оценки метода наименьших квадратов линейной модели
оценки метода наименьших квадратов линейной модели 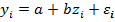 с
с  . При этом нужно помнить, что свойства оценок параметров и модели (получаемые, например, с помощью функции «Регрессия» в MS Excel) относятся к преобразованной линейной модели, а не к исходной нелинейной модели.
. При этом нужно помнить, что свойства оценок параметров и модели (получаемые, например, с помощью функции «Регрессия» в MS Excel) относятся к преобразованной линейной модели, а не к исходной нелинейной модели.
2. Регрессии нелинейные по параметрам разделяются на внутренне линейные и внутренне нелинейные модели. Внутренне линейные модели с помощью соответствующих преобразований приводятся к линейному виду и затем оцениваются методом наименьших квадратов. Внутренне нелинейные модели не могут быть приведены к линейному виду. Внутренне нелинейные модели оцениваются специальными методами. В работе рассматриваются только внутренне линейные модели.
Рассмотрим наиболее широко применяемые при моделировании социально-экономических процессов внутренне линейные модели регрессии и их преобразования к линейному виду.
Мультипликативная модель (степенная с постоянной эластичностью 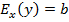 )
)
 ,
,
 – мультипликативная случайная ошибка регрессии. Эта модель нелинейная относительно оцениваемых параметров a и b. Прологарифмировав это уравнение, получим
– мультипликативная случайная ошибка регрессии. Эта модель нелинейная относительно оцениваемых параметров a и b. Прологарифмировав это уравнение, получим
 .
.
Введя новые величины 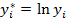 ,
,  ,
,  и
и 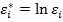 , получим линейное уравнение
, получим линейное уравнение
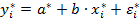 ,
,
в котором ошибки регрессии 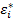 должны удовлетворять предпосылкам линейной регрессии. Получив МНК оценки
должны удовлетворять предпосылкам линейной регрессии. Получив МНК оценки  и
и  параметров линеаризованной модели, одновременно получаем оценку параметра b нелинейной модели, а оценка параметра a находится как
параметров линеаризованной модели, одновременно получаем оценку параметра b нелинейной модели, а оценка параметра a находится как  .
.
Экспоненциальная модель (с постоянным темпом прироста b )
 (или
(или 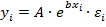 ).
).
Прологарифмировав получим 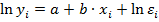 . Введя новые величины
. Введя новые величины 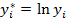 и
и 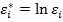 , получим линейное уравнение
, получим линейное уравнение
 ,
,
в котором ошибки регрессии 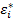 должны удовлетворять предпосылкам линейной регрессии. МНК оценки
должны удовлетворять предпосылкам линейной регрессии. МНК оценки  и
и  параметров линеаризованной модели являются оценками параметров исходной нелинейной модели.
параметров линеаризованной модели являются оценками параметров исходной нелинейной модели.
Экспоненциальная модель
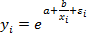 (или
(или  ).
).
Прологарифмировав получим  . Введя новую зависимую переменную
. Введя новую зависимую переменную 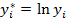 и новую объясняющую переменную
и новую объясняющую переменную 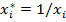 , получим линейное уравнение
, получим линейное уравнение
 .
.
МНК оценки  и
и  параметров линеаризованной модели являются оценками параметров исходной нелинейной модели.
параметров линеаризованной модели являются оценками параметров исходной нелинейной модели.
Показательная модель (с постоянным темпом прироста равным lnb )
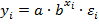
логарифмированием приводится к виду 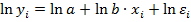 и введением новых величин
и введением новых величин 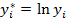 ,
,  и
и 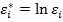 преобразуется в линейную модель
преобразуется в линейную модель  . Ошибки регрессии
. Ошибки регрессии 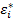 должны удовлетворять предпосылкам линейной регрессии. По МНК оценкам
должны удовлетворять предпосылкам линейной регрессии. По МНК оценкам  и
и  параметров линеаризованной модели, оценки параметров a и b показательной модели находятся как
параметров линеаризованной модели, оценки параметров a и b показательной модели находятся как  и
и  .
.
Обратная модель

приводится к линеаризованному виду 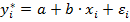 с помощью замены
с помощью замены 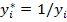 . Более сложная обратная модель (логистическая)
. Более сложная обратная модель (логистическая)

приводится к линеаризованному виду 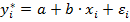 с помощью замены
с помощью замены  . В обеих случаях МНК оценки
. В обеих случаях МНК оценки  и
и  параметров линеаризованной модели являются оценками параметров обратной модели.
параметров линеаризованной модели являются оценками параметров обратной модели.
Примеры внутренне нелинейных моделей (не приводимых к линейным по параметрам зависимостям):  ,
,  ,
, 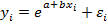 ,
, 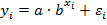 ,
,
 ,
,  .
.
Линеаризация многофакторных нелинейных регрессионных моделей производится с использованием тех же приемов. Например, производственная функция Кобба-Дугласа  логарифмированием приводится к виду
логарифмированием приводится к виду  и заменами
и заменами 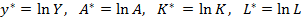 преобразуется к линейному по параметрам уравнение
преобразуется к линейному по параметрам уравнение 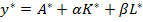 .
.
Для сопоставления различных линейных и нелинейных регрессионных моделей по их прогностическому качеству используются индекс корреляции (корреляционное отношение)

и средняя ошибка аппроксимации
 .
.
Здесь  – рассчитанные по уравнению регрессии значения зависимой переменной,
– рассчитанные по уравнению регрессии значения зависимой переменной,  – выборочная средняя значений зависимой переменной, n – объем выборки. Индекс корреляции характеризует разброс выборочных значений относительно линии регрессии
– выборочная средняя значений зависимой переменной, n – объем выборки. Индекс корреляции характеризует разброс выборочных значений относительно линии регрессии 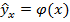 .
.  , чем больше значение
, чем больше значение  , тем меньше разброс выборочных значений вокруг линии регрессии (тем лучше качество подгонки уравнения регрессии к выборочным данным). Если
, тем меньше разброс выборочных значений вокруг линии регрессии (тем лучше качество подгонки уравнения регрессии к выборочным данным). Если  равно или близко к нулю, то оцененная модель непригодна, она не объясняет изменение зависимой переменной изменением объясняющей переменной, т. е. построенная модель не лучше модели
равно или близко к нулю, то оцененная модель непригодна, она не объясняет изменение зависимой переменной изменением объясняющей переменной, т. е. построенная модель не лучше модели 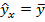 . Квадрат индекса корреляции называется коэффициентом детерминации
. Квадрат индекса корреляции называется коэффициентом детерминации  . Он показывает долю вариации зависимой переменной Y объясняемую вариацией фактора X в построенной модели регрессии. Средняя ошибка аппроксимации A характеризует среднее относительное отклонение выборочных значений от построенной линии регрессии
. Он показывает долю вариации зависимой переменной Y объясняемую вариацией фактора X в построенной модели регрессии. Средняя ошибка аппроксимации A характеризует среднее относительное отклонение выборочных значений от построенной линии регрессии 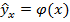 .
.
Статистическая значимость уравнения нелинейного регрессии проводится по F- критерию Фишера  , который имеет F-распределение Фишера-Снедекора с
, который имеет F-распределение Фишера-Снедекора с  и
и  степенями свободы, где
степенями свободы, где  – число коэффициентов в уравнении регрессии, а n – объем выборки. Оцененное уравнение нелинейной регрессии статистически незначимо, если вычисленное значение F- критерия меньше критического
– число коэффициентов в уравнении регрессии, а n – объем выборки. Оцененное уравнение нелинейной регрессии статистически незначимо, если вычисленное значение F- критерия меньше критического 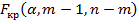 . Если
. Если  , то оцененное уравнение нелинейной регрессии статистически значимо, т.е. влияние фактора
, то оцененное уравнение нелинейной регрессии статистически значимо, т.е. влияние фактора 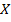 на исследуемый признак
на исследуемый признак  может быть описано оцененным уравнением нелинейной регрессии.
может быть описано оцененным уравнением нелинейной регрессии.  – квантиль уровня
– квантиль уровня 
 -распределения Фишера-Снедекора с
-распределения Фишера-Снедекора с  и
и  степенями свободы.
степенями свободы.
Содержание лабораторной работы.
1. Ввод данных и построение диаграммы рассеяния для подбора подходящей нелинейной по фактору или внутренне линейной регрессионной модели.
2. Построение линейной модели парной регрессии и нахождение для нее средней ошибки аппроксимации.
3. Выбор нелинейной модели, и приведение ее к линейному виду, преобразование переменных.
4. Оценка линеаризованной модели и ее значимости, нахождение оценок параметров нелинейной модели и запись оцененной нелинейной модели.
5. Построение прогнозов среднего зависимой переменной для выборочных значений фактора (регрессора), построение линии регрессии наложенной на диаграмму рассеяния, нахождение индекса корреляции и средней ошибки аппроксимации.
6. Проверка статистической значимости уравнения нелинейной регрессии.
7. Сравнение линейной и нелинейной регрессионных моделей.
8. Интерпретация модели и общее заключение.
Выполнение работы в MS Excel.
Построение в MS Excel парной нелинейной регрессии и сопоставление ее с линейной регрессией проведем на примере построения регрессионной зависимости себестоимости добычи единицы объема газа Y (центы) от процента жидкости в добываемом газе X. Данные наблюдений по десяти скважинам приведены в нижеследующей таблице.
| X | 13,3 | 16,9 | 19,9 | 23,2 | 26,3 | 28,7 | 30,1 | 35,1 | 37,4 | 42,6 |
| Y | 3,4 | 5,1 | 4,8 | 6,7 | 6,0 | 6,3 | 9,5 | 9,9 | 11,6 | 13,8 |
Ввод данных. В ячейках А1-А11 расположим значения Х, а в ячейках В1-В11 значения Y. Построение диаграммы рассеяния осуществляется также как в работе 3. По диаграмме рассеяния (рис. 9) можем предположить, что имеющиеся данные могут быть описаны линейной регрессией  или нелинейной регрессией (например, мультипликативной или экспоненциальной моделью). На рис.9 приведены также значения преобразованных переменных для мультипликативной и экспоненциальной модели и диаграммы рассеяния для новых переменных.
или нелинейной регрессией (например, мультипликативной или экспоненциальной моделью). На рис.9 приведены также значения преобразованных переменных для мультипликативной и экспоненциальной модели и диаграммы рассеяния для новых переменных.
Линейную регрессионную модель оценим следуя работе 3. Ее результаты приведены на рис. 10. Для вычисления средней ошибки аппроксимации  к таблице «Вывод остатков» добавим столбец для значений
к таблице «Вывод остатков» добавим столбец для значений  . В рассматриваемом примере этот столбец занимает ячейки D 54- D 64, см. рис.10. Для вычисления
. В рассматриваемом примере этот столбец занимает ячейки D 54- D 64, см. рис.10. Для вычисления  воспользуемся функцией ABC нахождения модуля числа в группе «Математические» вкладки «Формулы». Выделим ячейку D 55 и, учитывая расположение на листе величин
воспользуемся функцией ABC нахождения модуля числа в группе «Математические» вкладки «Формулы». Выделим ячейку D 55 и, учитывая расположение на листе величин  и
и  , в строке формул введем =ABS(C55/B2). По Enter в ячейке D 55 получим искомое значение. Копируя эту формулу в ячейки D 56- D 64, получим остальные значения
, в строке формул введем =ABS(C55/B2). По Enter в ячейке D 55 получим искомое значение. Копируя эту формулу в ячейки D 56- D 64, получим остальные значения 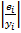 . Среднюю ошибку аппроксимации найдем, используя операцию нахождения среднего значения СРЗНАЧ в группе «Статистические» вкладки «Формулы». Для этого выделим ячейку Е55 и в строке формул введем =СРЗНАЧ( D 55: D 64)*100. По ОК получим искомое значение. В примере 14,96%, см. рис 10.
. Среднюю ошибку аппроксимации найдем, используя операцию нахождения среднего значения СРЗНАЧ в группе «Статистические» вкладки «Формулы». Для этого выделим ячейку Е55 и в строке формул введем =СРЗНАЧ( D 55: D 64)*100. По ОК получим искомое значение. В примере 14,96%, см. рис 10.

Рис. 9. Преобразования переменных и диаграммы рассеяния
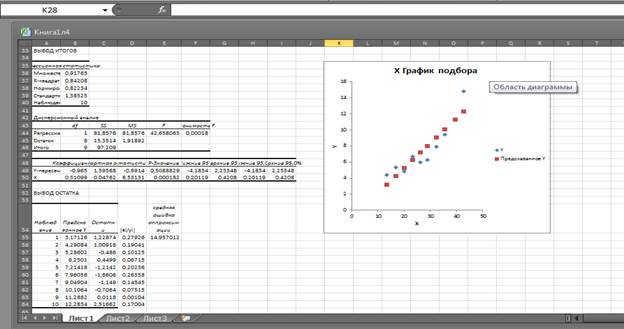
Рис. 10. Линейная регрессия
Выбор нелинейной модели, ее линеаризация и оценка параметров нелинейной модели. Для мультипликативной  и экспоненциальной
и экспоненциальной  моделей проведем необходимые преобразования переменных. Мультипликативная модель сводится к линейной введением новых переменных
моделей проведем необходимые преобразования переменных. Мультипликативная модель сводится к линейной введением новых переменных 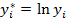 ,
,  ; а экспоненциальная заменой
; а экспоненциальная заменой 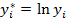 . Значения
. Значения  разместим в ячейках С1-С11, а значения
разместим в ячейках С1-С11, а значения 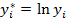 в ячейках D 1- D 11. Построим также диаграммы рассеяния для преобразованных переменных, близость выборочных точек к некоторой прямой свидетельствует о приемлемости рассматриваемой нелинейной регрессии, см. рис. 9. Оценки параметров линеаризованных моделей проведем также как и в работе 3. Результаты приведены на рис.11 – 12.
в ячейках D 1- D 11. Построим также диаграммы рассеяния для преобразованных переменных, близость выборочных точек к некоторой прямой свидетельствует о приемлемости рассматриваемой нелинейной регрессии, см. рис. 9. Оценки параметров линеаризованных моделей проведем также как и в работе 3. Результаты приведены на рис.11 – 12.
Мультипликативная модель. Результаты регрессии для линеаризованной модели  показывают значимость оцененного уравнения и его параметров. Для линеаризованной модели получены следующие оценки ее параметров
показывают значимость оцененного уравнения и его параметров. Для линеаризованной модели получены следующие оценки ее параметров  . Для нелинейной модели
. Для нелинейной модели  найдем оценки ее параметров: для нахождения оценки параметра
найдем оценки ее параметров: для нахождения оценки параметра 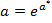 выделим, например, ячейку М92 и в строке формул введем =ЕХР(В86), в этой ячейке получим искомое значение
выделим, например, ячейку М92 и в строке формул введем =ЕХР(В86), в этой ячейке получим искомое значение  ; оценка параметра
; оценка параметра  для нелинейной модели совпадает с его значением для линеаризованной модели. Оцененная мультипликативная модель имеет вид
для нелинейной модели совпадает с его значением для линеаризованной модели. Оцененная мультипликативная модель имеет вид
 .
.
Нахождение прогнозных значений зависимой переменной по нелинейной модели, вычисление средней ошибки аппроксимации и индекса корреляции. К таблице «Вывод остатка», расположенной в примере в ячейках А93-С103, добавим следующие столбцы. В ячейках D93-D103 столбец «предсказанное по НМ» - прогнозных значений  В ячейках Е93-Е103 столбец «остатки по НМ» - значений остатков
В ячейках Е93-Е103 столбец «остатки по НМ» - значений остатков  нелинейной модели. В ячейках F93-F103 столбец
нелинейной модели. В ячейках F93-F103 столбец 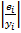 – относительных ошибок аппроксимации. В ячейках G93-G103 столбец «
– относительных ошибок аппроксимации. В ячейках G93-G103 столбец «  » - отклонений выборочных значений
» - отклонений выборочных значений  от их среднего
от их среднего  . В ячейках Н93-Н103 столбец «предсказанное
. В ячейках Н93-Н103 столбец «предсказанное  – сред.Y» - отклонений предсказанных значений
– сред.Y» - отклонений предсказанных значений  от среднего
от среднего  .
.
Вычисление прогнозного значения  . Выделим ячейку D 94 и в строке формул введем =EXP(B94).По Enter в этой ячейке получим искомое значение
. Выделим ячейку D 94 и в строке формул введем =EXP(B94).По Enter в этой ячейке получим искомое значение 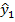 . Аналогично вычисляются другие значения
. Аналогично вычисляются другие значения  . Для вычисления остатков нелинейной модели
. Для вычисления остатков нелинейной модели  выделим ячейку Е94 и в строке формул введем =B2-D94, по Enter в этой ячейке получим искомое значение
выделим ячейку Е94 и в строке формул введем =B2-D94, по Enter в этой ячейке получим искомое значение  . Скопировав эту формулу в ячейки Е95-Е103, получим значения других остатков.
. Скопировав эту формулу в ячейки Е95-Е103, получим значения других остатков.
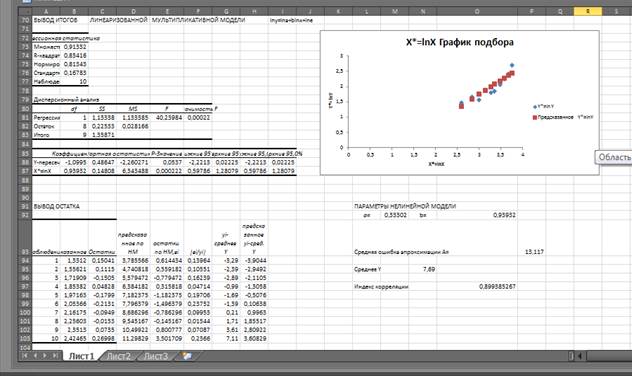
Рис. 11. Оценка нелинейной мультипликативной модели
Для вычисления относительных ошибок аппроксимации 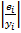 выделим ячейку F 94 и в строке формул введем =ABS(E94/B2), по Enter в этой ячейке получим искомое значение
выделим ячейку F 94 и в строке формул введем =ABS(E94/B2), по Enter в этой ячейке получим искомое значение  Скопировав эту формулу в ячейки F95-F103, получим остальные значения
Скопировав эту формулу в ячейки F95-F103, получим остальные значения 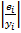 .
.
Для вычисления отклонений  найдем выборочное среднее
найдем выборочное среднее  . Выделив ячейку N 95 и введя в строке формул =СРЗНАЧ(B2:B11), получим значение выборочного среднего
. Выделив ячейку N 95 и введя в строке формул =СРЗНАЧ(B2:B11), получим значение выборочного среднего  , равное в примере 7,69. Выделив ячейку G 94 и введя в строке формул =B2-7,69, по Enter в этой ячейке получим
, равное в примере 7,69. Выделив ячейку G 94 и введя в строке формул =B2-7,69, по Enter в этой ячейке получим 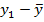 . Скопировав эту формулу в ячейки G95-G103, получим остальные значения
. Скопировав эту формулу в ячейки G95-G103, получим остальные значения  . Для нахождения отклонений предсказанных значений
. Для нахождения отклонений предсказанных значений  от среднего
от среднего  выделим ячейку Н94 и в строке формул введем =D94-7,69, по Enter в этой ячейке получим
выделим ячейку Н94 и в строке формул введем =D94-7,69, по Enter в этой ячейке получим 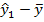 . Скопировав эту формулу в ячейки Н95-Н103, получим остальные значения
. Скопировав эту формулу в ячейки Н95-Н103, получим остальные значения  .
.
Среднюю ошибку аппроксимации мультипликативной модели найдем, используя вычисленные ранее относительные ошибки аппроксимации 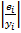 и функцию СРЗНАЧ вычисления выборочного среднего. В ячейку Р93 введем =СРЗНАЧ(F94:F103)*100. По Enter получим значение средней ошибки аппроксимации мультипликативной модели, равное в примере 13,117%.
и функцию СРЗНАЧ вычисления выборочного среднего. В ячейку Р93 введем =СРЗНАЧ(F94:F103)*100. По Enter получим значение средней ошибки аппроксимации мультипликативной модели, равное в примере 13,117%.
Нахождение индекса корреляции мультипликативной модели. Выделим ячейку О97, в строке формул введем =КОРЕНЬ(1-(СУММКВ(E94:E103))/СУММКВ(G94:G103)). По Enter получим в этой ячейке значение индекса корреляции, равное в примере 0,8996.
Экспоненциальная модель. Результаты регрессии для линеаризованной модели  приведены на рис.12. Они показывают значимость оцененного уравнения и его параметров. Оценки параметров линеаризованной модели
приведены на рис.12. Они показывают значимость оцененного уравнения и его параметров. Оценки параметров линеаризованной модели  являются также оценками параметров нелинейной модели
являются также оценками параметров нелинейной модели 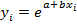 . Оцененная экспоненциальная модель имеет вид
. Оцененная экспоненциальная модель имеет вид  .
.
Для нахождения прогнозных значений зависимой переменной по экспоненциальной модели, вычисления средней ошибки аппроксимации и индекса корреляции к таблице «Вывод остатка», расположенной в примере в ячейках А131-С141, добавим следующие столбцы. В ячейках D131-D141 столбец «предсказанное по НМ» - прогнозных значений 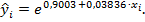 В ячейках Е131-Е141 столбец «остатки по НМ» - значений остатков
В ячейках Е131-Е141 столбец «остатки по НМ» - значений остатков  экспоненциальной модели. В ячейках F131-F141 столбец
экспоненциальной модели. В ячейках F131-F141 столбец 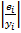 – относительных ошибок аппроксимации.
– относительных ошибок аппроксимации.
Вычисление прогнозных значения  . Выделим ячейку D 132 и введем в строке формул =EXP( B 124+ B 125* A 2). По Enter в этой ячейке получим искомое значение
. Выделим ячейку D 132 и введем в строке формул =EXP( B 124+ B 125* A 2). По Enter в этой ячейке получим искомое значение 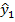 . Аналогично вычисляются другие значения
. Аналогично вычисляются другие значения  . Для вычисления остатков регрессии нелинейной модели,
. Для вычисления остатков регрессии нелинейной модели,  , выделим ячейку Е132 и в строке формул введем =B2-D132, по Enter в этой ячейке получим искомое значение
, выделим ячейку Е132 и в строке формул введем =B2-D132, по Enter в этой ячейке получим искомое значение  . Скопировав эту формулу в ячейки Е133-Е141, получим значения других остатков. Для вычисления относительных ошибок аппроксимации
. Скопировав эту формулу в ячейки Е133-Е141, получим значения других остатков. Для вычисления относительных ошибок аппроксимации 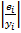 , выделим ячейку F 132 и в строке формул введем =ABS(E132/B2), по Enter в этой ячейке получим искомое значение
, выделим ячейку F 132 и в строке формул введем =ABS(E132/B2), по Enter в этой ячейке получим искомое значение  , копируя эту формулу в ячейки F95-F103, получим остальные значения
, копируя эту формулу в ячейки F95-F103, получим остальные значения 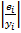 .
.

Рис.12. Оценка нелинейной экспоненциальной модели
Среднюю ошибку аппроксимации экспоненциальной модели найдем, используя вычисленные относительные ошибки аппроксимации 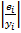 . Выделим ячейку Р132 и в строке формул введем =СРЗНАЧ(F132:F141)*100. По Enter получим значение средней ошибки аппроксимации мультипликативной модели, равное в примере 9,56%.
. Выделим ячейку Р132 и в строке формул введем =СРЗНАЧ(F132:F141)*100. По Enter получим значение средней ошибки аппроксимации мультипликативной модели, равное в примере 9,56%.
Нахождение индекса корреляции экспоненциальной модели. Выделим ячейку Р97 и в строке формул введем =КОРЕНЬ(1-(СУММКВ(E132:E141))/СУММКВ(G94:G103)). По Enter получим в этой ячейке значение индекса корреляции, равное в примере 0,957.
Построение графиков нелинейной регрессии и диаграммы рассеяния. Для совмещения диаграммы рассеяния с графиками мультипликативной и экспоненциальной уравнений регрессии скопируем в ячейки А146-156 выборочные значения  , в ячейки В146-156 выборочные значения
, в ячейки В146-156 выборочные значения  , в ячейки С146-156 вычисленные по мультипликативной модели значения зависимой переменной
, в ячейки С146-156 вычисленные по мультипликативной модели значения зависимой переменной  , в ячейки D146-156 вычисленные по экспоненциальной модели значения зависимой переменной
, в ячейки D146-156 вычисленные по экспоненциальной модели значения зависимой переменной  . В вкладке «Вставка» в группе «Диаграммы» выберем вид «Точечная», в группе «Макеты диаграмм» выберем «Макет 1», в группе «Данные» выберем «Выбрать данные». В открывшемся окне «Выбор источника данных» в поле «Диапазон данных для диаграммы» укажем ячейки с данными А147: D 156. По ОК получим необходимую диаграмму, см. рис. 13. Средствами MS Excel проводится корректировка заголовка и надписей осей на диаграмме.
. В вкладке «Вставка» в группе «Диаграммы» выберем вид «Точечная», в группе «Макеты диаграмм» выберем «Макет 1», в группе «Данные» выберем «Выбрать данные». В открывшемся окне «Выбор источника данных» в поле «Диапазон данных для диаграммы» укажем ячейки с данными А147: D 156. По ОК получим необходимую диаграмму, см. рис. 13. Средствами MS Excel проводится корректировка заголовка и надписей осей на диаграмме.
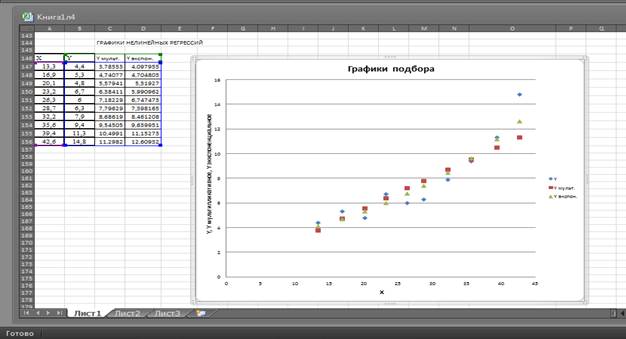
Рис. 13. Линии нелинейных регрессий и диаграмма рассеяния
Интерпретация модели и общее заключение. Построенная мультипликативная модель  значима и согласуется с выборочными данными. Об этом свидетельствуют значение индекса корреляции
значима и согласуется с выборочными данными. Об этом свидетельствуют значение индекса корреляции  и средняя ошибка аппроксимации
и средняя ошибка аппроксимации 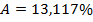 . Коэффициент детерминации
. Коэффициент детерминации  , т.е. 80,8% вариации себестоимости добычи единицы объема газа объясняется в этой модели вариацией процента жидкости в добываемом газе. Среднее относительное отклонение выборочных данных от линии регрессии составляет 13,12%, что больше допустимого уровня. Мультипликативная модель обладает постоянной эластичностью, равной параметру b . В построенной мультипликативной модели b =0,9393, следовательно, увеличение содержания процента жидкости на 1% приводит в среднем к увеличению себестоимости добычи газа на 0,9393%.
, т.е. 80,8% вариации себестоимости добычи единицы объема газа объясняется в этой модели вариацией процента жидкости в добываемом газе. Среднее относительное отклонение выборочных данных от линии регрессии составляет 13,12%, что больше допустимого уровня. Мультипликативная модель обладает постоянной эластичностью, равной параметру b . В построенной мультипликативной модели b =0,9393, следовательно, увеличение содержания процента жидкости на 1% приводит в среднем к увеличению себестоимости добычи газа на 0,9393%.
Экспоненциальная модель  также значима и лучше чем мультипликативная модель согласуется с выборочными данными. Об этом свидетельствуют значение индекса корреляции
также значима и лучше чем мультипликативная модель согласуется с выборочными данными. Об этом свидетельствуют значение индекса корреляции  и средняя ошибка аппроксимации
и средняя ошибка аппроксимации  . Коэффициент детерминации
. Коэффициент детерминации  , т.е. 91,58% вариации себестоимости добычи единицы объема газа объясняется в экспоненциальной модели вариацией процента жидкости в добываемом газе. Среднее относительное отклонение выборочных данных от линии регрессии составляет 9,53%, что является приемлемой ошибкой аппроксимации. Экспоненциальная модель обладает постоянным темпом прироста, равным параметру b . В построенной экспоненциальной модели b =0,03836, следовательно, увеличение содержания жидкости в добываемом газе на 1% приводит к увеличению себестоимости добычи газа на 3,836%.
, т.е. 91,58% вариации себестоимости добычи единицы объема газа объясняется в экспоненциальной модели вариацией процента жидкости в добываемом газе. Среднее относительное отклонение выборочных данных от линии регрессии составляет 9,53%, что является приемлемой ошибкой аппроксимации. Экспоненциальная модель обладает постоянным темпом прироста, равным параметру b . В построенной экспоненциальной модели b =0,03836, следовательно, увеличение содержания жидкости в добываемом газе на 1% приводит к увеличению себестоимости добычи газа на 3,836%.
Линейная регрессионная модель  дает среднюю ошибка аппроксимации 14,96% и коэффициент детерминации
дает среднюю ошибка аппроксимации 14,96% и коэффициент детерминации  , т.е. линейная модель объясняет только 84,2% вариации себестоимости добычи газа вариацией процента содержания в нем жидкости.
, т.е. линейная модель объясняет только 84,2% вариации себестоимости добычи газа вариацией процента содержания в нем жидкости.
Таким образом, из рассмотренных регрессионных зависимостей лучшими аппроксимационными свойствами обладает экспоненциальная модель 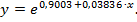
Контрольные вопросы.
1. В чем отличие регрессионных моделей нелинейных только по факторам и нелинейных по параметрам?
2. В чем отличие внутренне линейных и внутренне нелинейных регрессионных моделей?
3. Приведите примеры внутренне линейных моделей. Как осуществляется их линеаризация?
4. Как оцениваются параметры внутренне линейных моделей?
5. Приведите примеры внутренне нелинейных моделей.
6. Какие показатели корреляции используются при анализе нелинейных взаимосвязей?
7. Как определяется и что характеризует средняя ошибка аппроксимации?
8. Как определяется и что характеризует индекс корреляции?
9. По каким критериям отбираются нелинейные регрессионные модели?
10. Как определяется и что характеризует коэффициент эластичности?
11. Как определяется темп прироста и что он характеризует?
|
из
5.00
|
Обсуждение в статье: Лабораторная работа № 4. Нелинейная парная регрессия |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

