НАИБОЛЕЕ ПОПУЛЯРНЫЕ СХЕМЫ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ: «ОБЩАЯ ШИНА», «ЛИНЕЙКА», «КОЛЬЦО», «ТОР», «РЕШЕТКА».

Схемы обмена между вычислителями:

1. Общая шина. Структура вычислительной сети типа «Общая шина» описывается графом GS=(M, S*), где M ={m_i}, i=0, …, N-1 – множество вычислителей, N≥3, S* в каждый момент времени t_k = {t₁, …, t_k} состоит из одного ребра S_i,j (i,j M), а множество вершин t_k определяет моменты реконфигурации сети.

2. Линейка. Структура ВС типа «Линейка» описывается графом GS=(M, S*), где M ={m_i}, i=0, …, N-1 – множество вычислителей, N≥3, S* состоит из ребер S_i,(i+1), i=0, …, N-2.

*Каждый вычислитель кроме первого и последнего, связан друг с другом. Минус такой схемы: Отказ одного вычислителя приводит всю систему к сбою.

3. Кольцо. Структура ВС типа «Кольцо» описывается графом GS=(M, S*), где M ={m_i}, i=0, …, N-1 – множество вычислителей, N≥3, S* состоит из ребер S_i,(i+1)modN, i=0, …, N-1.

*Каждый вычислитель связан друг с другом. Функция mod(N) – строит ребро между первым и последним вычислителями.

4. Решетка. Структура ВС типа «Решетка» описывается графом GS=(M, S*), где M={m_i}, i= 0, …,N-1, N>5; S* состоит из множества ребер S_i,k j {0, …,Y-1}, k {0, …, L-1}, причем L×Y=N.

Ребро проводиться между вершинами, определяемыми декартовым произведением [j] ×[k]. Две вершины соединяются ребром, если их декартовы произведения отличаются друг от друга на 1 по координате k или j соответственно.

Тор – см. след. вопрос.

СТРУКТУРА ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ ТИПА ДВУМЕРНЫЙ ТОР, N-МЕРНЫЙ ДВОИЧНЫЙ ГИПЕРКУБ.

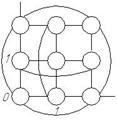Двумерный тор.

*Здесь между собой соединяются граничные вычислители (возможно, все), т.е. те, которые имеют max или min координату по одной из осей. (минус: появляются дополнительные шины). Другими словами можно сказать, что двумерный тор- это ВС «2D-решетка», противоположные грани которой соединены, обеспечивая обмен данными между первым и последним элементами строки/столбца.

Структура ВС типа «двумерный тор» описывается графом GS=(M,S*), где M= 0, …, N-1, N≥7; S* состоит из ребер S_i,k j {0, …,Y-1}, k {0, …, L-1}, причем L×Y=N.

Ребро проводиться между вершинами, определяемыми декартовым произведением [j] ×[k]. Две вершины соединяются ребром, если их декартовы произведения отличаются друг от друга на 1 по любой координате или на L-1 по координате k или на Y-1 по координате j.

N-мерный двоичный гиперкуб.

Структура ВС типа «двоичный гиперкуб» описывается графом GS=(M,S*), где М={m_i}, i=0, …,N-1, N≥4, вершины имеют номера N_i=2^p, p=0,1,…,n-1, где n – размерность гиперкуба.

Каждая вершина V_i задается двоичным числом

q(V_i)=p_vi,0… p_vi,n-1.

Между вершинами V_i и V_j проводиться ребро, если их двоичные номера q(V_i) и q(V_j) различаются только одним разрядом.

РЕАЛИЗАЦИЯ ОБМЕНА ИНФОРМАЦИЕЙ В СТРУКТУРЕ ТИПА «ОБОБЩЕННЫЙ ND-КУБ» И «ND-ТОР»

Обобщенный nd-куб.

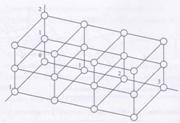Структура ВС типа «обобщенный nd-куб» описывается графом GS=(M,S*), где М={m_i}, i=0, …,N-1, N≥5.

По каждой координате j=1, …,n откладываются точки (вершины) с номерами 0,1,…,N_j-1, где N_j – размерность куба по координате j.

Множество вершин задается декартовым произведением [N₁-1] ×[N₂-1] ×…×[N_n-1]; N₁ ∙N₂ ∙…∙N_n=N. Две вершины соединяются ребром, если декартовы произведения отличаются друг от друга на 1 по координате N_j, j {1, …, n}.

Обобщенный nd-тор.

Структура ВС типа «Обобщенный nd-тор» описывается графом GS=(M,S*), где М={m_i}, i=0, …,N-1.

По каждой координате j=1,…,n, вводятся точки 0,1, …, N_j-1, где N_j размерность тора по координате j.

Множество вершин графа задается декартовым произведением [N₁-1] ×[N₂-1] ×…×[N_n-1].

Множество ребер сети S* строиться следующем образом: две вершины соединяются ребром, если их декартово произведение отличается друг от друга на 1 или на N_j -1 по координате j. (картинки 2D и 3D на след. странице)