|
Главная |
Теорема 4.5. Теорема синусов для трехгранного угла.
|
из
5.00
|
Справедливо равенство

где alpha, beta, gamma – плоские углы трехгранного угла; A, B, C – противолежащие им двугранные углы.
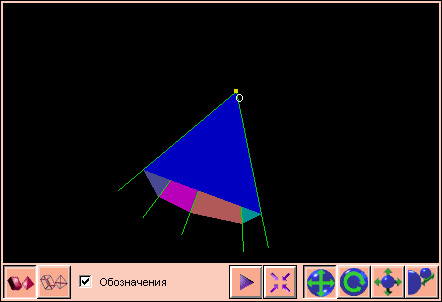
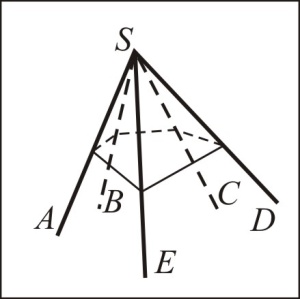
Пусть дан трехгранный угол с вершиной S и ребрами SA, SB и SC, двугранные углы при которых равны соответственно A, B и C. Возьмем какую-нибудь точку P на ребре SA. Пусть O – ее проекция на плоскость SBC. Пусть R – проекция точки O на ребро SC, а Q – проекция точки O на ребро SB (чертеж 4.4.5).

На рисунке изображен тот случай, когда точка O попала вовнутрь угла BSC. Однако отметим, что все наши рассуждения не изменятся, если эта точка попадет вне или на сторону угла BSC. Из теоремы о трех перпендикулярах следует, что угол PRO равен C, а угол PQO равен B, поскольку каждый из них есть линейный угол двугранного угла при соответствующем ребре. Найдем длину отрезка PO двумя способами. С одной стороны, PO = PR sin C = SP sin beta sin C. С другой стороны, имеем PO = PQ sin B = SP sin gamma sin B. Приравниваем:
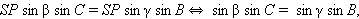
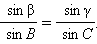
Второе равенство устанавливается аналогично. Теорема доказана.
Определение 4.6.
Несколько плоских углов с общим началом O, из которых никакие два не лежат в одной плоскости, образуют многогранный угол (чертеж 4.4.5). Эти плоские углы при вершине многогранного угла называются гранями, а стороны этих углов – ребрами, точка O – вершиной многогранного угла. По числу граней многогранный угол называется трехгранным, четырехгранным и т.д. Если все грани многогранного угла находятся с одной стороны от каждой из плоскостей его граней, угол называется выпуклым. В данном курсе рассматриваются только выпуклые многогранные углы.
| |
| Чертеж 4.4.6. |
Теорема 4.6.
Каждый плоский угол многогранного угла меньше суммы всех остальных его плоских углов.
Теорема 4.7.
Сумма плоских углов выпуклого многогранного угла меньше 360°.








Определение. Многогранным углом называется геометрическая фигура, являющаяся объединением плоских углов, удовлетворяющих перечисленным ниже требованиям, и части пространства, для которой эти углы служат границей. Требования к плоским углам многогранного угла:
1) Никакие два угла не имеют общих точек, кроме их общей вершины или стороны.
2) У каждого из таких углов каждая сторона является общей со стороной только одного такого угла.
3) Никакие два угла с общей стороной не лежат в одной плоскости.
Плоские углы, образующие многогранный угол, называются его гранями, а их стороны – рёбрами.
 Из определения следует, что вершины всех плоских углов совпадают. Эта точка называется вершиной многогранного угла.
Из определения следует, что вершины всех плоских углов совпадают. Эта точка называется вершиной многогранного угла.
Многогранный угол называется выпуклым, если он лежит по одну сторону от плоскости каждой его грани.
По числу граней многогранный угол может быть трёхгранным, четырёхгранным, …, n-гранным.
На рисунке изображён пятигранный угол SABCDE. Его вершиной является точка S, гранями – плоские углы ASB, BSC, CSD, DSE и ESA, рёбрами – лучи SA, SB, SC, SD, SE.
Двугранный угол исключён из числа многогранных углов в виду неопределённости в выборе его вершины.
Каждые две грани, имеющие общее ребро, определяют двугранный угол многогранного угла.
В элементарной математике обычно рассматриваются выпуклые многогранные углы, плоские углы которых меньше 180°.
 Два трёхгранных угла называются равными, если равны их соответственные элементы: плоские углы и двугранные углы.
Два трёхгранных угла называются равными, если равны их соответственные элементы: плоские углы и двугранные углы.
Точка X называется внутренней точкой трёхгранного угла SABC, если луч SX пересекает плоскость ABC в точке, которая является внутренней точкой треугольника ABC.
Геометрическое место внутренних точек трёхгранного угла, равноудалённых от его граней, называется пространственной биссектрисой этого угла.
Свойства многогранных углов.
Теорема 1 (Свойство плоских углов трехгранного угла). Градусная мера каждого плоского угла трехгранного угла меньше суммы градусных мер двух других плоских углов.

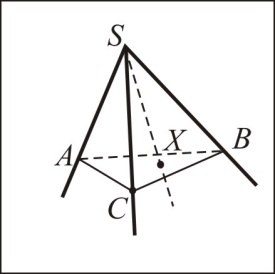
1) Рассмотрим трехгранный угол SABC. Пусть угол ASB его наибольший плоский угол. Покажем, что 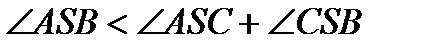 .
.
2) Построим в плоскости ASB угол ASK, равный углу ASC. От точки S на луче SK отложим отрезок SM. На луче SC отложим SN = SM. Через точку M в плоскости ASB проведем прямую до пересечения с лучами SA и SB в точках R и P. Соединим точки R и P с точкой N. Получим равные треугольники SRM и SRN (по двум сторонам и углу между ними). Из равенства треугольников следует равенство сторон RM = RN.
3) Согласно неравенству треугольника в треугольнике RPN RP < RN + NP, т.е. RM+ MP < RN + NP, откуда
MP < NP.
4) В треугольниках SPM и SPN по две равные стороны, следовательно, против большей стороны лежит больший угол, т.е. 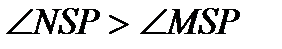 , прибавляя к обеим частям этого неравенства по равным углам RSM и RSN, получим
, прибавляя к обеим частям этого неравенства по равным углам RSM и RSN, получим  .‡
.‡
Теорема 2 (Свойство плоских углов многогранного угла). Сумма градусных мер всех плоских углов выпуклого многогранного угла меньше 360º.
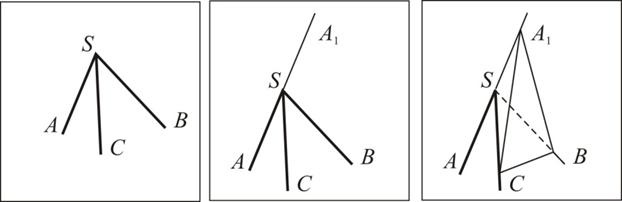 Доказательство проведем для трехгранного угла.
Доказательство проведем для трехгранного угла.
1) Рассмотрим трехгранный угол SABC. Построим луч SA1, противоположный лучу SA.
2) Рассмотрим трехгранный угол SA1BC. Его плоскими углами являются ÐBSC, ÐA1SC=  , ÐA1SB=
, ÐA1SB=  . Применим к ним теорему 1, получим:
. Применим к ним теорему 1, получим:

 +
+  ,т.е
,т.е  . ‡
. ‡
Теорема 3.Если два плоских угла трехгранного угла равны, то их общее ребро проектируется на биссектрису третьего плоского угла или ее продолжение.
Доказательство оформить самостоятельно.
Рассмотрим зависимости между плоскими и двугранными углами многогранного угла.
Теорема косинусов для трехгранного угла. Косинус плоского угла трехгранного угла равен произведению косинусов двух остальных плоских углов, сложенному с произведением синусов этих же углов и косинуса двугранного угла, противолежащего этому плоскому двугранному углу.
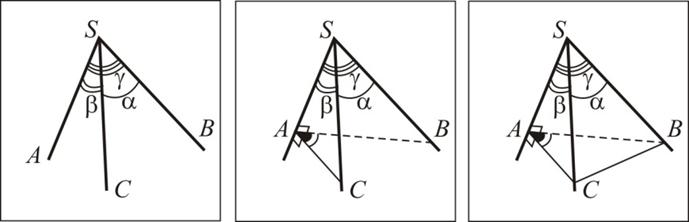 1) Пусть в трехгранном угле SABC плоские углы ÐCSB = α, ÐASC =β, ÐASB = γ , а двугранный угол при ребре SА равен A. Докажем, что:
1) Пусть в трехгранном угле SABC плоские углы ÐCSB = α, ÐASC =β, ÐASB = γ , а двугранный угол при ребре SА равен A. Докажем, что:

2) Построим линейный угол двугранного угла при ребре SА. (Из точки A проведем перпендикуляры AB и AС к ребру SA в гранях ASB и ASС.)
3) D BAC : по теореме косинусов  (1).
(1).
D BSC:по теореме косинусов 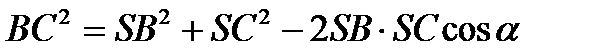 (2).
(2).
Из равенств (1) и (2) следует  =
= 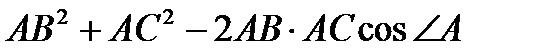 (3)
(3)
4) DASB (ÐA = 90°):  ,
,
DASС (ÐA = 90°):  ,
,
Из равенства 3, получим: 
Разделив обе части этого равенства на произведение SB∙SC, получим
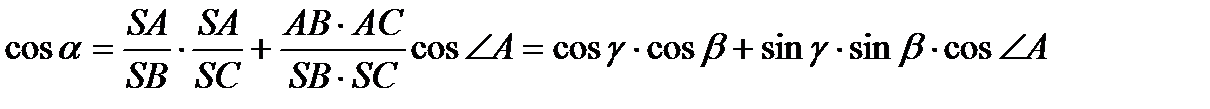 .‡
.‡
Доказательство для случая тупых плоских углов следует из приведенного доказательства заменой данных тупых углов смежными им углами.
Теорема синусов для трехгранного угла.В трехгранном угле синусы плоских углов пропорциональны синусам противолежащих им двугранных углов, т.е. 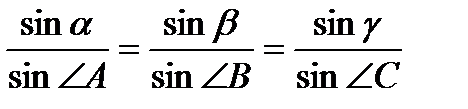 .
.
Доказательство следует из теоремы косинусов для трёхгранного угла. Проведите его самостоятельно по следующему плану:
1. Выразите косинусы двугранных углов, используя формулы теоремы косинусов для трёхгранного угла.
2. Выразите квадраты косинусов этих углов.
3. Выразите квадраты синусов этих углов, используя равенство  .
.
4. Убедитесь в равенстве отношений, указанных в условии теоремы.
Многогранники
Конечная система многогранников, заданных в определенном порядке, называется цепочкой, соединяющей многоугольники, если два смежных многоугольника (Рi и Pi+1 ) где i=1, 2,…n-1)не лежат в одной плоскости и имеют общую сторону (связывающая сторона), а любые два несмежных многоугольника PiPmi<m-1 , 3 ≤m≤n, либо не имеют ни одной общей точки, либо имеют только общую вершину, которая является концом всех связывающих сторон пар многоугольников PiPi+1…Pm-1, Pm.
1.1.Геометрическое тело. Определение многогранника. Виды многогранников
Определение. Точка M фигуры F, расположенной в пространстве, называется граничной точкой фигуры F,если на сколь угодно малом расстоянии от точки M найдутся точки, как принадлежащие фигуре F, так и не принадлежащие этой фигуре.
Множество всех граничных точек фигуры называется её границей.
Определение. Точка M фигуры F, расположенной в пространстве, называется внутренней точкой фигуры F,если существует шар с центром в этой точке, каждая точка которого принадлежит фигуре F.
Множество всех внутренних точек фигуры называется её внутренностью.
Фигура называется ограниченной, если все её точки принадлежат некоторому шару.
Определение. Геометрическим телом называется ограниченная фигура в пространстве, обладающая следующими свойствами:
1) у неё есть внутренние точки, и любые две из них можно соединить ломаной, каждая точка которой является внутренней точкой фигуры;
2) фигура содержит свою границу и её граница совпадает с границей её внутренности.
Граница тела называется его поверхностью.
Определение. Многогранником называется геометрическое тело, поверхность которого состоит из конечного числа многоугольников, любые два смежные из которых не лежат в одной плоскости.
Многоугольники, образующие границу многогранника, называются гранями, их стороны – рёбрами, а вершины – вершинами многогранника.
Многогранники подразделяются на выпуклые и невыпуклые многогранники.
Многогранник называется выпуклым, если он расположен по одну сторону от каждой из плоскостей, содержащих его грани. Многогранник, не являющийся выпуклым, называется невыпуклым.


Свойства многогранников
1.Любые две внутренние точки многогранника можно соединить ломаной, целиком состоящей из внутренних точек.
2.Любая ломаная, в частности отрезок, соединяющая внутреннюю точку многогранника с точкой внешней по отношению к нему, пересекает его поверхность по крайней мере в общей точке.
3. Какова бы ни была внутренняя точка многогранника, существует шар с центром в этой точке, внутри которого лежат все точки многогранника.
4. Любой луч, исходящий из внутренней точки многогранника, пересекает его поверхность по крайне мере в одной точке.
5.Любые две внешние точки относительно многогранника можно соединить ломаной, целиком состоящей из внешних точек.
В школьных учебниках геометрии многогранниками обычно называются тела, поверхности которых состоят из конечного числа многоугольников, называемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника.
Многогранник называется выпуклым, если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками содержит и соединяющий их отрезок.
На рисунке 1 приведены примеры выпуклых и невыпуклых многогранников.

Рассмотрим некоторые свойства выпуклых многогранников.
Свойство 1.В выпуклом многограннике все грани являются выпуклыми многоугольниками.
Доказательство. Пусть F - какая-нибудь грань многогранника M, и A, B – точки, принадлежащие грани F (рис. 2). Из условия выпуклости многогранника M, следует, что отрезок AB целиком содержится в многограннике M. Поскольку этот отрезок лежит в плоскости многоугольника F, он будет целиком содержаться и в этом многоугольнике, т.е. F - выпуклый многоугольник.

Свойство 2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.
Доказательство. Пусть M - выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку Sмногогранника M, т.е. такую его точку, которая не принадлежит ни одной грани многогранника M. Соединим точку S с вершинами многогранника M отрезками (рис. 3). Заметим, что в силу выпуклости многогранника M, все эти отрезки содержатся в M. Рассмотрим пирамиды с вершиной S, основаниями которых являются грани многогранника M. Эти пирамиды целиком содержатся в M, и все вместе составляют многогранник M.
Свойство 3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.
Доказательство. Предположим противное, т.е. существуют точки A и B многогранника M, лежащие по разные стороны от плоскости некоторой его грани N (рис. 4). Рассмотрим пирамиды с вершинами в точках A, B, основаниями которых является грань N. В силу выпуклости многогранника, эти пирамиды целиком в нем содержатся. Это противоречит тому, что N является гранью многогранника M.
Для выпуклых многогранников имеет место свойство, связывающее число его вершин, ребер и граней, доказанное в 1752 году Леонардом Эйлером, и получившее название теоремы Эйлера.
Прежде чем его сформулировать рассмотрим известные нам многогранники и заполним следующую таблицу, в которой В - число вершин, Р - ребер и Г - граней данного многогранника:
| Название многогранника | В | Р | Г |
| Треугольная пирамида | |||
| Четырехугольная пирамида | |||
| Треугольная призма | |||
| Четырехугольная призма | |||
| n-угольная пирамида | n+1 | 2n | n+1 |
| n-угольная призма | 2n | 3n | n+2 |
| n-угольная усеченная пирамида | 2n | 3n | n+2 |
Из этой таблицы непосредственно видно, что для всех выбранных многогранников имеет место равенство В - Р + Г = 2. Оказывается, что это равенство справедливо не только для этих многогранников, но и для произвольного выпуклого многогранника.
Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство
В - Р + Г = 2,
где В - число вершин, Р - число ребер и Г - число граней данного многогранника.
Доказательство.Для доказательства этого равенства представим поверхность данного многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости. Получим многоугольник (образованный ребрами удаленной грани многогранника), разбитый на более мелкие многоугольники (образованные остальными гранями многогранника).
Заметим, что многоугольники можно деформировать, увеличивать, уменьшать или даже искривлять их стороны, лишь бы при этом не происходило разрывов сторон. Число вершин, ребер и граней при этом не изменится.
Докажем, что для полученного разбиения многоугольника на более мелкие многоугольники имеет место равенство
(*) В - Р + Г ' = 1,
где В – общее число вершин, Р – общее число ребер и Г ' – число многоугольников, входящих в разбиение. Ясно, что Г '= Г – 1, где Г – число граней данного многогранника.
Докажем, что равенство (*) не изменится, если в каком-нибудь многоугольнике данного разбиения провести диагональ (рис. 5, а). Действительно,после проведения такой диагонали в новом разбиении будет В вершин, Р+1 ребер и количество многоугольников увеличится на единицу. Следовательно, имеем
В - (Р + 1) + (Г '+1) = В – Р + Г '.

Пользуясь этим свойством, проведем диагонали, разбивающие входящие многоугольники на треугольники, и для полученного разбиения покажем выполнимость равенства (*) (рис. 5, б). Для этого будем последовательно убирать внешние ребра, уменьшая количество треугольников. При этом возможны два случая:
а) для удаления треугольника ABC требуется снять два ребра, в нашем случае AB и BC;
б) для удаления треугольника MKN требуется снять одно ребро, в нашем случае MN.
В обоих случаях равенство (*) не изменится. Например, в первом случае после удаления треугольника граф будет состоять из В – 1 вершин, Р – 2 ребер и Г ' – 1 многоугольника:
(В - 1) - (Р + 2) + (Г ' – 1) = В – Р + Г '.
Самостоятельно рассмотрите второй случай.
Таким образом, удаление одного треугольника не меняет равенство (*). Продолжая этот процесс удаления треугольников, в конце концов, мы придем к разбиению, состоящему из одного треугольника. Для такого разбиения В = 3, Р = 3, Г ' = 1 и, следовательно, B – Р + Г ' = 1. Значит, равенство (*) имеет место и для исходного разбиения, откуда окончательно получаем, что для данного разбиения многоугольника справедливо равенство (*). Таким образом, для исходного выпуклого многогранника справедливо равенство В - Р + Г = 2.
Пример многогранника, для которого не выполняется соотношение Эйлера, показан на рисунке 6. Этот многогранник имеет 16 вершин, 32 ребра и 16 граней. Таким образом, для этого многогранника выполняется равенство В – Р + Г = 0.
Используя соотношение Эйлера, докажем, следующее свойство выпуклых многогранников.
Свойство 4.В любом выпуклом многограннике найдется грань с числом ребер меньшим или равным пяти.
Действительно, в каждой вершине многогранника сходится, по крайней мере, три ребра. Если количество вершин равно В и в каждой из них сходится три ребра, то общее число ребер будет больше или равно 3В : 2. Делить на два нужно потому, что при таком подсчете ребер мы каждое ребро посчитаем дважды – один раз, как ребро выходящее из одной его вершины, а второй раз, как ребро, выходящее из второй его вершины. Таким образом, для любого многогранника имеет место неравенство 3В  2Р.
2Р.
Обозначим через Гn число граней с n ребрами. Тогда Г = Г3 + Г4 + Г5 + Г6 + … . Каждая треугольная грань имеет три ребра и число треугольных граней равно Г3. Поэтому общее число ребер в треугольных гранях равно 3Г3. Аналогично, общее число ребер в четырехугольных гранях равно 4Г4и т. д.
Поскольку каждое ребро многогранника содержится ровно в двух гранях, то при таком подсчете ребер, мы каждое ребро посчитаем дважды и, следовательно, будет иметь место равенство 2Р = 3Г3+ 4Г4 + 5Г5 + 6Г6 + … .
Воспользуемся равенством 6В – 6Р + 6Г = 12, получающимся умножением обеих частей сооотношения Эйлера на 6. По доказанному выше, имеет место неравенство 6В  4Р и, следовательно, неравенство 6Г – 2Р
4Р и, следовательно, неравенство 6Г – 2Р  12. С другой стороны, 6Г = 6Г3 + 6Г4 + 6Г5 + 6Г6 + … , 2Р = 3Г3 + 4Г4 + 5Г5 + 6Г6 + … . Подставляя эти выражения в неравенство, получим неравенство 3Г3 + 2Г4 + Г5 + 0Г6 – Г7 – …
12. С другой стороны, 6Г = 6Г3 + 6Г4 + 6Г5 + 6Г6 + … , 2Р = 3Г3 + 4Г4 + 5Г5 + 6Г6 + … . Подставляя эти выражения в неравенство, получим неравенство 3Г3 + 2Г4 + Г5 + 0Г6 – Г7 – …  12. В левой части, начиная с Г7 стоят отрицательные числа. Поэтому для того, чтобы вся сумма была больше или равна 12 нужно, чтобы хотя бы одно из чисел Г3 или Г4 или Г5 было отлично от нуля, т.е. в многограннике существовала грань с соответствующим числом ребер.
12. В левой части, начиная с Г7 стоят отрицательные числа. Поэтому для того, чтобы вся сумма была больше или равна 12 нужно, чтобы хотя бы одно из чисел Г3 или Г4 или Г5 было отлично от нуля, т.е. в многограннике существовала грань с соответствующим числом ребер.
Правильные многогранники
Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники, и все многогранные углы равны.
Рассмотрим возможные правильные многогранники и прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники (рис. 7). В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также правильным тетраэдром, или просто тетраэдром, что в переводе с греческого языка означает четырехгранник.
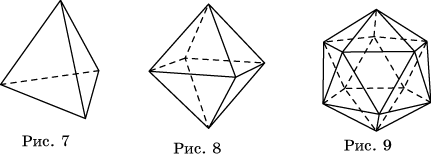
Многогранник, гранями которого являются правильные треугольники, и в каждой вершине сходится четыре грани, изображен на рисунке 8. Его поверхность состоит из восьми правильных треугольников, поэтому он называется октаэдром.
Многогранник, в каждой вершине которого сходится пять правильных треугольников, изображен на рисунке 9. Его поверхность состоит из двадцати правильных треугольников, поэтому он называется икосаэдром.
Заметим, что поскольку в вершинах выпуклого многогранника не может сходиться более пяти правильныхтреугольников, то другихправильных многогранников, гранями которых являются правильные треугольники, не существует.
Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба (рис. 10), других правильных многогранников, у которых гранями являются квадраты не существует. Куб имеет шесть граней и поэтому называется также гексаэдром.
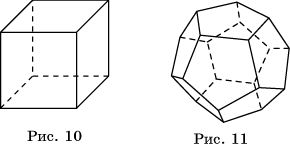
Многогранник, гранями которого являются правильные пятиугольники, и в каждой вершине сходится три грани, изображен на рисунке 11. Его поверхность состоит из двенадцати правильных пятиугольников, поэтому он называется додекаэдром.
Рассмотрим понятие правильного многогранника с точки зрения топологии науки, изучающей свойсва фигур, не зависящих от различных деформаций без разрывов. С этой точки зрения, например, все треугольники эквивалентны, так как один треугольник всегда может быть получен из любого другого соответствующим сжатием или растяжением сторон. Вообще все многоугольники с одинаковым числом сторон эквивалентны потой же причине.
Как в такой ситуации определить понятие топологически правильного многогранника? Иначе говоря, какие свойства в определении правильного многогранника являются топологически устойчивыми и их следует оставить, а какие не являются топологически устойчивыми и их следует отбросить.
В определении правильного многогранника количество сторон и количество граней являются топологически устойчивыми, т.е. не меняющимися при непрерывных деформациях. Правильность же многоугольников не являетсятопологически устойчивым свойством. Таким образом, мы приходим к следующему определению.
Выпуклый многогранник называется топологически правильным, если его гранями являются многоугольники с одним и тем же числом сторон и в каждой вершине сходится одинаковое число граней.
Два многогранника называются топологически эквивалентными, если один из другого можно получить непрерывной деформацией.
Например, все треугольные пирамиды являются топологически правильными многогранниками, эквивалентнымимежду собой. Все параллелепипеды также являются эквивалентными между собой топологически правильными многогранниками.Не являются топологически правильными многогранниками, например, четырехугольныепирамиды.
Выясним вопрос о том, сколько существует не эквивалентных между собой топологически правильных многогранников.
Как мы знаем, существует пять правильных многогранников: тетраэдр, куб, октаэдр, икосаэдр и додекаэдр. Казалось бы, топологически правильных многогранников должно быть гораздо больше. Однако оказывается, что никаких других топологически правильных многогранников, не эквивалентных уже известным правильным, не существует.
Для доказательства этого воспользуемся теоремой Эйлера. Пусть дан топологически правильный многогранник, гранями которого являются n - угольники, и в каждой вершине сходится m ребер. Ясно, что n и m больше или равны трех. Обозначим, как и раньше, В - число вершин, Р - число ребер и Г - число граней этого многогранника. Тогда
nГ = 2P; Г = 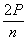 ; mB = 2P; В =
; mB = 2P; В =  .
.
По теореме Эйлера, В - Р + Г = 2 и, следовательно,

Откуда Р =  .
.
Из полученного равенства, в частности, следует, что должно выполняться неравенство 2n + 2m – nm > 0, которое эквивалентно неравенству (n – 2)(m – 2) < 4.
Найдем всевозможные значения n и m, удовлетворяющие найденному неравенству, и заполним следующую таблицу
| N m | |||
| B=4, Р=6, Г=4 тетраэдр | В=6, Р=12, Г=8 октаэдр | В=12, Р=30, Г=20 икосаэдр | |
| В=8, Р=12, Г=4 куб | Не существует | Не существует | |
| В=20, Р=30, Г=12 додекаэдр | Не существует | Не существует |
Например, значения n = 3, m = 3 удовлетворяют неравенству (n – 2)(m – 2) < 4. Вычисляя значения Р, В и Г по приведенным выше формулам, получим Р = 6, В = 4, Г = 4.
Значения n = 4, m = 4 не удовлетворяют неравенству (n – 2)(m – 2) < 4 и, следовательно, соответствующего многогранника не существует.
Самостоятельно проверьте остальные случаи.
Из этой таблицы следует, что возможными топологически правильными многогранниками являются только правильные многогранники, перечисленные выше, и многогранники, им эквивалентные.
ТЕТРАЭДР
Тетраэдр - это частный случай правильной треугольной пирамиды.
Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.
Грань тетраэдра и вершина, не принадлежащая ей, называются противоположными.
Ребра тетраэдра, не имеющие общих вершин, называются противоположными.
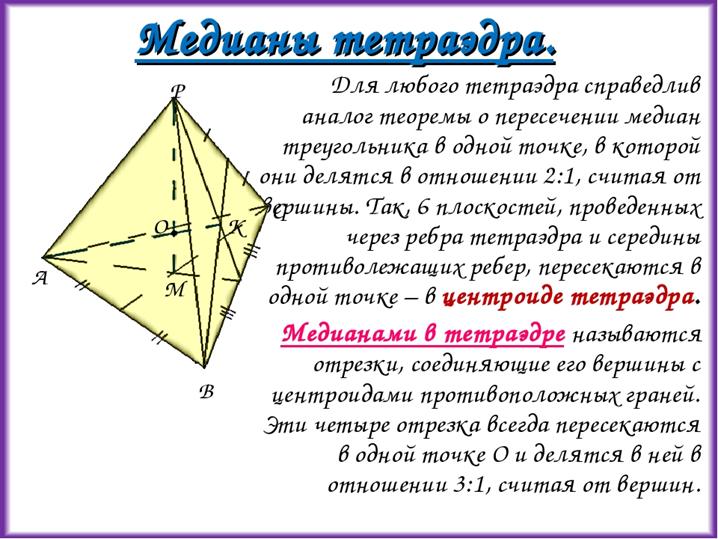
Медиана тетраэдра - это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).
Бимедиана тетраэдра - это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).
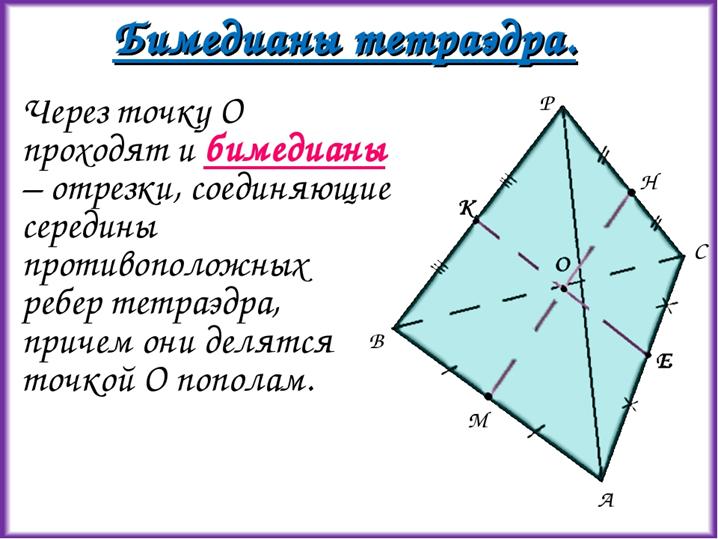
Высота тетраэдра - это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).
Свойства тетраэдра.
1)Четыре отрезка, каждый из которых соединяет вершину тетраэдра с точкой пересечения медиан противоположной грани, пересекаются в одной точке, которая делит каждый из этих отрезков в отношении 3:1, считая от вершины.
2) Середины отрезков, соединяющих середины противоположных ребер тетраэдра совпадают
3)Шесть плоскостей, каждая из которых проходит через ребро тетраэдра и середину противоположного ребра, пересекаются в одной точке.
Теорема. Прямые, содержащие две высоты тетраэдра, пересекаются тогда и только тогда, когда ребро, из концов которого проведены эти высоты, перпендикулярно противоположному ребру.
Следствия:
1. прямые, содержащие две высоты тетраэдра пересекаются в точке Р. Тогда прямые, содержащие две другие высоты, также пересекаются в некоторой точке Q.
2.Если прямые, содержащие четыре высоты тетраэдра, пересекаются в одной точке, то противоположные ребра тетраэдра взаимно перпендикулярны. Обратно, если две пары противоположных ребер тетраэдра перпендикулярны, то прямые, содержащие четыре высоты тетраэдра, пересекаются в одной точке.
3.Две пары противоположных ребер тетраэдра попарно перпендикулярны. Тогда и третья пара противоположных ребер тетраэдра перпендикулярна.
Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.
Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.
Типы тетраэдров.
Правильный тетраэдр - это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр - это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
- Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.
- Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
- Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
- Каркасный тетраэдр — тетраэдр, который таким условиям:
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
- Соразмерный тетраэдр, бивысоты у него одинаковы.
- Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
Формулы для определения элементов тетраэдра.
Высота тетраэдра:
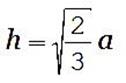
где h - высота тетраэдра, a - ребро тетраэдра.
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
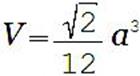
где V - объем тетраэдра, a - ребро тетраэдра.
Основные формулы для правильного тетраэдра:

Где S - Площадь поверхности правильного тетраэдра;
V – объем;
h - высота, опущенная на основание;
r - радиус вписанной в тетраэдр окружности;
R - радиус описанной окружности;
a - длина ребра.
ПРИЗМА
Призма — это многогранник, у которого две грани (основания призмы) — равные многоугольники с соотвественно параллельными сторонами. Остальные грани — параллелограммы, плоскости которых параллельны одной прямой.
 Призма
Призма
Параллелограммы и т.д. называются боковыми гранями. Высотой призмы называется перпендикуляр опущенный из любой точки одного основания.на плоскость другого. Призма называется треугольной четырехугольной и т.д., смотря по тому, лежит ли в основании треугольник, четырехугольник и т.д.
Если боковые ребра призмы перпендикулярны к плоскости основания, то — призма прямая. Если нет — призма наклонная. Если в прямой призме основание — правильный многоугольник — призма правильная.
Перпендикулярное сечение призмы — это такое сечение, которое образовано плоскостью перпендикулярной к её боковому ребру.
Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды. Перпендикуляр опущенный из вершины пирамиды на ее основание, называется высотой пирамиды. Пирамида называется треугольной, четырехугольной, и т.д., если основанием пирамиды является треугольник, четырехугольник и т.д. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и т.д.
 Пирамида, Усеченная Пирамида
Пирамида, Усеченная Пирамида
⇐Предыдущая19202122232425262728Следующая ⇒
Дата добавления: 2014-02-24; просмотров: 6036; Опубликованный материал нарушает авторские права? | Защита персональных данных | ЗАКАЗАТЬ РАБОТУ
Не нашли то, что искали? Воспользуйтесь поиском:
|
Лучшие изречения: Студент - че
|
из
5.00
|
Обсуждение в статье: Теорема 4.5. Теорема синусов для трехгранного угла. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы