 |
Главная |
Теория аппроксимации финитными функциями Стренга-Фикса
|
из
5.00
|
Изложим основные идеи этой теории для функций одной переменной с регулярными конечными элементами.
Область  покрываем равномерной сеткой
покрываем равномерной сеткой
 , [p] – целая часть p.
, [p] – целая часть p.
Конечные элементы 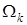 выберем как отрезки длиной
выберем как отрезки длиной  с центром в точке
с центром в точке  :
:  . Если
. Если  , смежные элементы не пересекаются и их длина равна
, смежные элементы не пересекаются и их длина равна  : если
: если  , то длина пересечения равна
, то длина пересечения равна  , длина
, длина 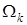 равна
равна  ; при
; при  – длина пересечения
– длина пересечения  , длина
, длина 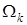 равна
равна  . Заметим, что такое покрытие полностью удовлетворяет условиям (2.2). Все базисные финитные функции с носителями
. Заметим, что такое покрытие полностью удовлетворяет условиям (2.2). Все базисные финитные функции с носителями 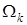 выберем одинаковой формы как сдвиги одной «стандартной» финитной функции
выберем одинаковой формы как сдвиги одной «стандартной» финитной функции  :
:
 ;
;  (2.5)
(2.5)
Если «стандартная» функция нормирована к единице, то ее сдвиги записываются в виде
 (2.6)
(2.6)
Теорема Стренга-Фикса (один из вариантов)
Допустим, что  . В этом случае для
. В этом случае для 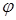 существует преобразование Фурье:
существует преобразование Фурье:
прямое  обратное
обратное 
Допустим, что для преобразования Фурье стандартной финитной функции 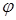 выполнено условие
выполнено условие
 и
и  при
при  (2.7)
(2.7)
(т.е. в  точках
точках  имеет нули
имеет нули 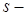 й кратности).
й кратности).
Тогда существуют такие  , что при
, что при 
 .
.
Это значит, что если, например, подобрать 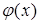 , у которой условия теоремы выполняются для
, у которой условия теоремы выполняются для  , то аппроксимация самой функции
, то аппроксимация самой функции  имеет порядок
имеет порядок 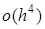 , аппроксимация ее первой производной
, аппроксимация ее первой производной 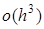 , второй –
, второй – 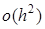 .
.
Наличие такой центральной теоремы, а также еще ряда доказанных Стренгом-Фиксом теорем, в частности о существовании функций, удовлетворяющих условиям (2.7), дает алгоритм для построения базисных финитных функций, обладающих необходимыми аппроксимационными свойствами.
B-сплайны Шёнберга
В вычислительной математике B-сплайном называют сплайн-функцию, имеющую наименьший носитель для заданной степени, порядка гладкости и разбиения области определения. Фундаментальная теорема устанавливает, что любая сплайн-функция для заданной степени, гладкости и области определения может быть представлена как линейная комбинация B-сплайнов той же степени и гладкости на той же области определения. [1] Термин B-сплайн был введён И. Шёнбергом и является сокращением от словосочетания «базисный сплайн». [2] B-сплайны могут быть вычислены с помощью алгоритма де Бора, обладающего устойчивостью.
В системах автоматизированного проектирования и компьютерной графике термин B-сплайн часто описывает сплайн-кривую, которая задана сплайн-функциями, выраженными линейными комбинациями B-сплайнов.
Когда узлы равноудалены друг от друга, говорят, что B-сплайн является однородным, в противном случае его называют неоднородным.
Когда количество узлов совпадает со степенью сплайна, B-сплайн вырождается в кривую Безье. Форма базисной функции определяется расположением узлов. Масштабирование или параллельный перенос базисного вектора не влияет на базисную функцию.
Сплайн содержится в выпуклой оболочке его опорных точек.
Базисный сплайн степени n:  .
.
не обращается в нуль только на промежутке [ti, ti+n+1], то есть:
 . (3.1)
. (3.1)
Другими словами, изменение одной опорной точки влияет только на локальное поведение кривой, а не на глобальное, как в случае кривых Безье.
Базисная функция может быть получена из полинома Бернштейна
|
из
5.00
|
Обсуждение в статье: Теория аппроксимации финитными функциями Стренга-Фикса |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

