 |
Главная |
Пространство функций со скалярным произведением.
|
из
5.00
|
Функция ƒ(x) называется кусочно-непрерывной на отрезке [a, b], если она непрерывна на этом отрезке, за исключением, может быть, конечного числа точек, где она имеет разрывы первого рода. Такие точки можно складывать и умножать на действительные числа и получать как результат снова кусочно-непрерывные на отрезке [a, b] функции.
Скалярным произведением двух кусочно-непрерывных на [a, b] (a < b) функций ƒ и φ будем называть интеграл
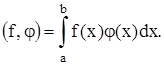 (11)
(11)
Очевидно для любых кусочно-непрерывных на [a, b] функций ƒ , φ , ψ выполняются свойства:
1) (ƒ , φ ) =( φ, ƒ );
2) (ƒ , ƒ ) и из равенства (ƒ , ƒ ) = 0 следует, что ƒ(x) =0 на [a, b], исключая, быть может, конечное число точек x;
3) (α ƒ + β φ , ψ) = α (ƒ , ψ) + β ( φ , ψ),
где α, β – произвольные действительные числа.
Множество всех кусочно-непрерывных функций, определенных на отрезке [a, b], для которых введено скалярное произведение по формуле (11), мы будем обозначать, 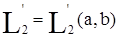 и называть пространством
и называть пространством 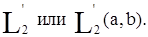
Замечание 1.
В математике называют пространством 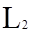 =
= 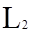 (a, b) совокупность функций ƒ(x), интегрируемых в лебеговом смысле на [a, b] вместе со своими квадратами, для которых введено скалярное произведение по формуле (11). Рассматриваемое пространство
(a, b) совокупность функций ƒ(x), интегрируемых в лебеговом смысле на [a, b] вместе со своими квадратами, для которых введено скалярное произведение по формуле (11). Рассматриваемое пространство 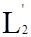 есть часть
есть часть 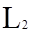 . Пространство
. Пространство 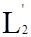 обладает многими свойствами пространства
обладает многими свойствами пространства 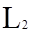 , но не всеми.
, но не всеми.
Из свойств 1), 2), 3) следует важное неравенство Буняковского | (ƒ , φ ) |≤ (ƒ , ƒ )½ (φ , φ ) ½, которое на языке интегралов выглядит так:
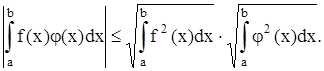
Величина
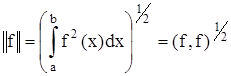
называется нормой функции f.
Норма обладает следующими свойствами:
1) || f || ≥ 0, при этом равенство может быть только для нулевой функции f = 0, т. е. функции, равной нулю, за исключением, быть может, конечного числа точек;
2) || ƒ + φ || ≤ || ƒ(x) || || φ ||;
3) || α ƒ || = | α | · || ƒ ||,
где α – действительное число.
Второе свойство на языке интегралов выглядит так:
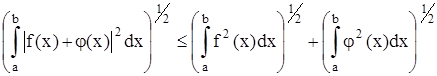
и называется неравенством Минковского.
Говорят, что последовательность функций { f n }, принадлежит к 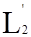 ,сходится к функции принадлежит
,сходится к функции принадлежит 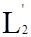 в смысле среднего квадратического на [a, b] (или ещё по норме
в смысле среднего квадратического на [a, b] (или ещё по норме 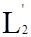 ), если
), если
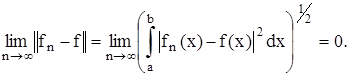
Отметим, что если последовательность функций ƒn (x) сходится равномерно к функции ƒ(x) на отрезке [a, b], то для достаточно больших n разность ƒ(x) - ƒn (x) по абсолютной величине должна быть мала для всех х из отрезка [a, b].
В случае же, если ƒn (x) стремится к ƒ(x)в смысле среднего квадратического на отрезке [a, b], то указанная разность может и не быть малой для больших n всюду на [a, b]. В отдельных местах отрезка [a, b] эта разность может быть и велика, но важно только, чтобы интеграл от её квадрата по отрезку [a, b] был мал для больших n.
Пример. Пусть на [0, l ] заданна изображенная на рисунке непрерывная кусочно-линейная функция ƒn (x) (n = 1, 2,…), причем
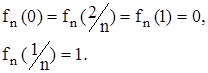
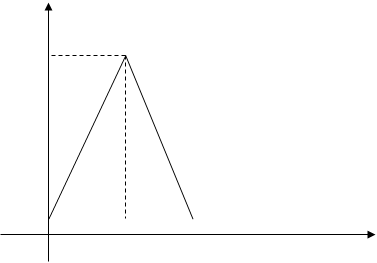 |
(Бугров, стр. 281, рис. 120)
При любом натуральном n
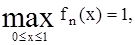
и, следовательно, эта последовательность функций, хотя и сходится к нулю при n → ∞, но неравномерно. Между тем
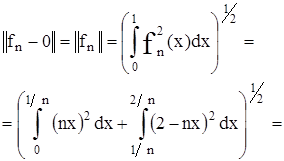

т. е. последовательность функций {fn (х)} стремится к нулю в смысле среднего квадратического на [0, 1].
Из элементов некоторой последовательности функций ƒ1, ƒ2, ƒ3,… (принадлежащих 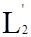 ) построим ряд
) построим ряд
ƒ1 + ƒ2 + ƒ3 +… (12)
Сумма первых его n членов
σ n = ƒ1 + ƒ2 + … + ƒn
есть функция, принадлежащая к 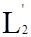 . Если случится, что в
. Если случится, что в 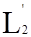 существует функция ƒ такая, что
существует функция ƒ такая, что
|| ƒ- σn || → 0 (n → ∞),
то говорят, что ряд (12) сходится к функции ƒ в смысле среднего квадратического и пишут
ƒ = ƒ1 + ƒ2 + ƒ3 +…
Замечание 2.
Можно рассматривать пространство 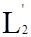 =
= 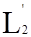 (a, b) комплекснозначных функций ƒ(x) = ƒ1(x) + iƒ2(x), где ƒ1(x) и ƒ2(x) – действительные кусочно – непрерывные на [a, b] функции. В этом пространстве функции умножаются на комплексные числа и скалярное произведение функций ƒ(x) = ƒ1(x) + iƒ2(x) и φ(х) = φ1(х) +i φ2(х) определяется следующим образом:
(a, b) комплекснозначных функций ƒ(x) = ƒ1(x) + iƒ2(x), где ƒ1(x) и ƒ2(x) – действительные кусочно – непрерывные на [a, b] функции. В этом пространстве функции умножаются на комплексные числа и скалярное произведение функций ƒ(x) = ƒ1(x) + iƒ2(x) и φ(х) = φ1(х) +i φ2(х) определяется следующим образом:
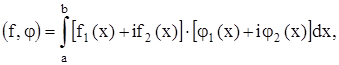
а норма ƒ определяется как величина
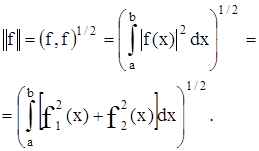
|
из
5.00
|
Обсуждение в статье: Пространство функций со скалярным произведением. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

