 |
Главная |
Отношения множеств. Виды отношений и их свойства
|
из
5.00
|
Элементы множества, как правило, находятся в каком-либо отношении друг относительно друга. Эти отношения можно задать в виде неполных предложений — предикатов, например, «меньше, чем...», «больше, чем ...», «эквивалентно», «конгруэнтно» и т. п.
Тот факт, что некоторый элемент  находится в каком-либо отношении к элементу того же множества xj , математически записывают как XiRxj , где R — символ отношения.
находится в каком-либо отношении к элементу того же множества xj , математически записывают как XiRxj , где R — символ отношения.
Отношение из двух элементов множества X называют бинарным. Бинарные отношения множеств X и Y представляют собой некоторое множество упорядоченных пар (х, у), образованных декартовым произведением X х Y . В общем случае можно говорить не только о множестве упорядоченных пар, но и о множестве упорядоченных троек, четверок элементов и т. д., т. е. о парных отношениях, получаемых в результате декартова произведения  , где п — размерность n-строчек.
, где п — размерность n-строчек.
Рассмотрим основные виды отношений — отношения эквивалентности, порядка и доминирования.
Некоторые элементы множеств можно считать эквивалентными в том случае, когда любой из этих элементов при определенных условиях можно заменить другим, т. е. данные элементы находятся вот-ношении эквивалентности. Примерами отношений эквивалентности являются отношения параллельности на множестве прямых какой-либо плоскости; подобия на множестве треугольников; принадлежности к одной функциональной группе микросхем или к одному классу типоразмеров и т. д.
Термин «отношение эквивалентности» будем применять при выполнении следующих условий:
1) каждый элемент эквивалентен самому себе;
2) высказывание, что два элемента являются эквивалентными, не требует уточнения того, какой из элементов рассматривается первым, а какой вторым;
3) два элемента, эквивалентные третьему, эквивалентны между собой.
Введем для обозначения эквивалентности символ ~, тогда рассмотренные условия можно записать следующим образом:
1) х ~ х (рефлективность);
2) х ~ у  у ~ х (симметричность);
у ~ х (симметричность);
3) х ~ у и у ~ z  х ~ z (транзитивность).
х ~ z (транзитивность).
Следовательно, отношение R называют отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Пусть некоторому элементу х  X эквивалентно некоторое подмножество элементов А
X эквивалентно некоторое подмножество элементов А  X , тогда это подмножество образует класс эквивалентности, эквивалентный х. Очевидно, что все элементы одного и того же класса эквивалентности эквивалентны между собой (свойство транзитивности). Тогда всякий элемент х
X , тогда это подмножество образует класс эквивалентности, эквивалентный х. Очевидно, что все элементы одного и того же класса эквивалентности эквивалентны между собой (свойство транзитивности). Тогда всякий элемент х  Х может находиться в одном и только одном классе эквивалентности, т. е. в этом случае множество X разбивается на некоторое непересекающееся подмножество классов эквивалентности
Х может находиться в одном и только одном классе эквивалентности, т. е. в этом случае множество X разбивается на некоторое непересекающееся подмножество классов эквивалентности  , где J — некоторое множество индексов.
, где J — некоторое множество индексов.
Таким образом, каждому отношению эквивалентности на множестве X соответствует некоторое разбиение множества X на классы  .
.
Часто сталкиваются с отношениями, которые определяют некоторый порядок расположения элементов множества. Например, в процессе автоматизированного конструирования требуется вводить множество одних исходных данных раньше или позже, чем множество других. При этом может оказаться, что элементы одного множества больше или меньше элементов другого и т. д. Во всех этих случаях можно расположить элементы множества X или группы элементов в некотором порядке (например, в виде убывающей или возрастающей последовательности), т. е. ввести отношение порядка на множестве X.
Различают отношения строгого порядка, для которых применяют символы  и отношения нестрогого порядка, где используют символы
и отношения нестрогого порядка, где используют символы  . Эти отношения характеризуются следующими свойствами:
. Эти отношения характеризуются следующими свойствами:
для отношения строгого порядка:
х < X — ложно (антирефлексивность);
х<У, а У<х — взаимоисключаются (несимметричность);
x<у и у < x  x < z — (транзитивность);
x < z — (транзитивность);
для отношения нестрогого порядка:
х  X— истинно (рефлексивность);
X— истинно (рефлексивность);
х  у и у
у и у  х
х  х = у — (антисимметричность);
х = у — (антисимметричность);
х  у и у
у и у  z
z  x у
x у  z — (транзитивность).
z — (транзитивность).
Множество X называют упорядоченным, если любые два элемента х и у этого множества сравнимы, т. е. если для них выполняется одно из условий: х < у, х = у, у < х.
Упорядоченное множество называют кортежем. В общем случае кортеж — это последовательность элементов, т. е. совокупность элементов, в которой каждый элемент занимает вполне определенное место. Элементы упорядоченного множества называются компонентами кортежа. Примерами кортежа может служить упорядоченная последовательность чисел арифметической или геометрической прогрессий, последовательность технологических операций при изготовлении какого-либо радиоэлектронного изделия, упорядоченная последовательность установочных позиций печатной платы для закрепления конструктивных элементов.
Во всех этих множествах место каждого элемента вполне определено и не может произвольно изменяться.
При обработке конструкторской информации на ЭВМ часто используют отношения доминирования. Говорят, что х  X доминирует над у
X доминирует над у 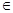 X , т. е. х>>у, если элемент х в чем-либо превосходит (имеет приоритет) элемент у того же множества. Например, под х можно понимать один из списков данных, который должен поступить на обработку первым. При анализе нескольких конструкций РЭА какой-либо из них должен быть отдан приоритет, так как эта конструкция обладает лучшими, с нашей точки зрения, свойствами, чем другие, т. е. конструкция х доминирует над конструкцией у.
X , т. е. х>>у, если элемент х в чем-либо превосходит (имеет приоритет) элемент у того же множества. Например, под х можно понимать один из списков данных, который должен поступить на обработку первым. При анализе нескольких конструкций РЭА какой-либо из них должен быть отдан приоритет, так как эта конструкция обладает лучшими, с нашей точки зрения, свойствами, чем другие, т. е. конструкция х доминирует над конструкцией у.
Свойство транзитивности при этом не имеет места. Действительно, если, например, конструкцию х по каким-либо одним параметрам предпочли конструкции у, а конструкцию у по каким-либо другим параметрам предпочли конструкции z, то отсюда еще не следует, что конструкции х должно быть отдано предпочтение по сравнению с конструкцией г.
Отображение множеств. Одним из основных понятий теории множеств является понятие отображения. Если заданы два непустых множества X и Y , то закон, согласно которому каждому элементу x  X ставится в соответствие элемента
X ставится в соответствие элемента  , называют однозначным отображением X в Y или функцией, определенной на X и принимающей значение на Y .
, называют однозначным отображением X в Y или функцией, определенной на X и принимающей значение на Y .
На практике приходится иметь дело и с многозначными отображениями множества X на множестве Y , которые определяют закон, согласно которому каждому элементу х  X ставится в соответствие некоторое подмножество
X ставится в соответствие некоторое подмножество  , называемое образом элементов. Возможны случаи, когда Гх = 0.
, называемое образом элементов. Возможны случаи, когда Гх = 0.
Пусть задано некоторое подмножество А  X . Для любого х
X . Для любого х  А образом х является подмножество
А образом х является подмножество  . Совокупность всех элементов Y , являющихся образами для всех х в А, назовем образом множества А и будем обозначать ГА. В этом случае
. Совокупность всех элементов Y , являющихся образами для всех х в А, назовем образом множества А и будем обозначать ГА. В этом случае 
|
из
5.00
|
Обсуждение в статье: Отношения множеств. Виды отношений и их свойства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

