Построения иными инструментами

1. Построения одним циркулем. Во многих случаях построения, проводимые циркулем, оказываются точнее, чем построения, проводимые линейкой.

Итальянский учений Л. Маскерони (1750-1800) и датский ученый Г.Мор (1640-1697) исследовали конструктивные возможности циркуля и доказали следующую теорему.

Теорема (Мора-Маскерони). Любая геометрическая задача на построение фигуры из конечного числа точек, разрешимая циркулем и линейкой может быть решена при наличии только циркуля.

Пояснения: 1) имеется в виду, что фигура состоит из конечного числа точек, окружностей, отрезков, лучей прямых; 2) циркулем конечно, нельзя построить прямую, отрезок, луч, здесь имеется в виду, что циркулем можно сделать их известными (прямая известна, если известны две ее точки; отрезок известен, если известны два его конца; луч известен, если известна начальная точка и точка, через которую проходит луч).

Доказательство опускаем.

2. Построения одной линейкой.

Построения одной линейкой исключительно ограничены. Например, отрезок нельзя разделить пополам. Но если на плоскости задана окружность, возможности увеличиваются.

Справедлива теорема. Всякая геометрическая задача на построение фигуры, состоящей из конечного числа точек, разрешимая циркулем и линейкой, может быть решена одной линейкой, если на плоскости построена окружность и отмечен ее центр (т.е. воли воспользоваться циркулем один раз). Это теорема Штейнера, иногда называют ее теоремой Понселе-Штейнера.

3. Построения двусторонней линейкой

Пример. Разделить данный угол пополам.

 

 

Проводим параллели, ОС - биссектриса

Оказывается, справедлива теорема

Всякая геометрическая фигура, состоящая из конечного числа точек, которая может быть построена циркулем и линейкой, может быть построена только двусторонней линейкой.

4. Построения с помощью прямого угла.

Пример. Построить центр начерченной окружности. Всякая геометрическая фигура, состоящая из конечного числа точек, которая может быть построена циркулем и линейкой, может быть построена только прямым углом. Это же верно для любого угла.

 

Пример 2. Дан ΔАВС; требуется построить три окружности так, чтобы каждая из них касалась двух других окружностей и двух сторон треугольника (задача Мальфатти). Считаем задачу решенной (фиг. 1). Пусть точка О будет центром вписанной в треугольник окружности (радиуса r). Радиусы кругов К и L обозначим соответственно через r₁ и r₂. Из точек К, О, L опустим перпендикуляры на сторону АВ и таким путем построим точки D, Е, F. Положим AE = s, BE = t, AD = x, BF = y.

 

Фиг. 2

 

Если мы проведем KG || AB, то

 

LG = r₂ – r₁ и KG =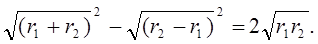

 

Из подобия 7) треугольников ADK и AEO следует, что

 

аналогично этому и , что вытекает из подобия треугольников BFL и ВЕО.

AB = AD + DF + FB,

 

следовательно:

 

=

 

или (подставляя вместо r₁ и r₂ полученные для них выражения)

 

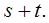= (1)

 

Если опустим из точек L, М,О перпендикуляры на сторону ВС и положим РС = и и QC = z, то получится равенство

 

2) = t + u;

 

аналогично мы получим равенство и для третьей стороны :

 

3) = u + s.

Таким образом, мы имеем три уравнения для определения трех неизвестных х, у, z.

Мальфатти сообщает решения этих трех уравнений,:

 

Если подставить эти значения в вышеприведенные уравнения, то они удовлетворят последним. Путь, которым Мальфатти нашел решения, чрезвычайно сложен, как он сам указывает.

Геометрическое же построение величин х, у, z представляется чрезвычайно простым, ибо

 

 

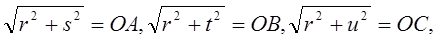
вследствие чего отрезки эти, равно как и отрезки s, t, r, u, r, легко могут быть построены.

Если же теперь построить выражение

 

x = ОА — m, у = ОБ — m,

z = OC - m (фиг. 2).

 

Пример 3. Даны три окружности K₁, K₂, К₃, коих центры лежат на одной прямой; радиус каждой из окружностей К₁, К₂ равен r₂. Последние две окружности имеют одно и то же центральное расстояние а от окружности К₁{r₁). Требуется построить все окружности, которые касаются трех данных (фиг. 3).

 

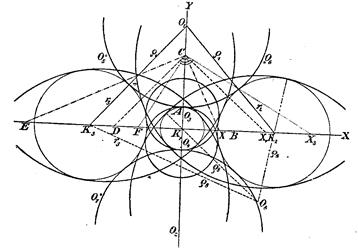
Фиг.3.

 

Для того, чтобы решить эту задачу вычислением, мы кладем в основание прямоугольную систему координат. При этом уравнения данных окружностей таковы:

 

К₁ … х²+у² = ,

K₂ … (x - a)² + y² =

K₃ … (x + a)² + y² =

 

Уравнение же каждой из искомых окружностей имеет вид:

 

(x - p_i)² + (y - q_i)² = ρ_i².

 

Для круга О₁ (фиг. 3) легко могут быть получены три уравнения, определяющие три неизвестные велиeчины p₁, q₁, ρ₁; именно, из условий

 

вытекают равенства

 

 

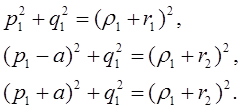
Из двух последних следует, что p₁ = 0, а отсюда уже непосредственно вытекает:

 

(1)

 

ибо радиус круга О₂ равен радиусу ρ₁ круга О₁ (фиг. 3).

Окружность О₃ касается окружностей К₂ и К₃ извне, а окружности К₁ — изнутри; таким образом, имеют место равенства

 

 

Отсюда получается

(2)

 

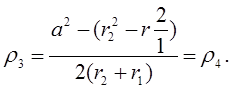
Для окружности О₅ имеют место равенства

 

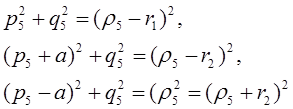
откуда получается:

 

 

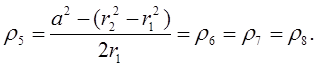
Построение может быть выполнено по следующему плану. Строим по порядку (фиг. 3):

 

AB = r2, BC = a,

 

тогда

 

 

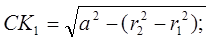
если затем построить

 

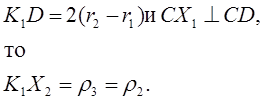
Аналогично построим

 

1. Весьма удобным методом для решения геометрических задач на построение является метод геометрических мест.

Он основывается на следующем: стараются свести всю задачу к нахождению некоторой точки X, что в большей части случаев сделать не трудно.

Точка X определяется двумя условиями, вытекающими из требования задачи. Если устранить первое из условий, то существует не одна только точка X, но бесчисленное множество таких точек, составляющих в совокупности некоторую линию, некоторое геометрическое место. Если же устранить второе условие и ограничиться первым, то получится другое геометрическое место. Каждая точка пересечения этих двух геометрических мест удовлетворяет требованиям задачи.

2. Является необходимым предварительно изучить некоторые геометрические места. Мы приведем наиболее простые и вместе с тем наиболее употребительные из них.

a) Геометрическое место точек, находящихся от данной точки на данном расстоянии, есть окружность, описанная из данной точки, как из центра, радиусом, равным данному расстоянию.

b) Геометрическое место точек, находящихся на данном расстоянии от данной прямой, состоит из двух прямых, проведенных параллельно данной прямой, на данном от нее расстоянии.

c) Геометрическое место точек, равноотстоящих от двух данных точек А и В, есть прямая, перпендикулярная к отрезку АВ в его середине. (Симметраль точек А и В).

d) Геометрическое место точек, равноотстоящих от двух данных прямых, состоит из двух взаимно перпендикулярных прямых делящих пополам углы между данными прямыми (биссектрисы).

e) Геометрическим местом точек, из которых отрезок АВ виден под данным углом а, является дуга окружности, стягиваемая* отрезком АВ (построение ясно из фиг. 4).

 

Фиг. 4 Фиг. 5

 

f) Геометрическое место точек, расстояния которых от двух данных точек находятся в данном отношении m : n, есть некоторая, окружность (фиг. 5)

При этом

 

 

Откуда по известной теореме получается , что < APP₁ = < P₁PB.

Имеет место также пропорция

 

AP₁:P₁B = AP₂:BP₂

Четыре такие точки называются, как известно, четырьмя гармоническими точками.

g) Геометрическое место точек, расстояния которых от двух данных прямых находятся в данном отношении m : n, образуется двумя прямыми линиями х и у, проходящими через точку пересечения данных прямых (фиг. б).

h) Геометрическое место точек, квадраты расстояний которых от двух данных точек А и В сохраняют постоянную разность d², есть прямая, перпендикулярная к отрезку АВ.

 

Фиг. 6 Фиг.7

 

Доказательство: Пусть точка Р₁ (фиг. 7) обладает указанным свойством, так что

 

 

Если опустить из точки P₁ на АВ перпендикуляр и взять на нем произвольную точку Р₁ то

 

Из h) может быть выведено следствие, которое позже для нас будет важно. Мы лишь предпошлем ему краткое замечание:

а) Как известно, справедливо следующее предложение: „Если через точку Р (фиг. 8а, 8_Ь) провести секущие к окружности, то постоянно

 

РА .РА' = РВ.РВ' = ... "

 

Эго постоянное произведение называется степенью точки Р в отношении данной окружности; степень равна d² — r², где d есть расстояние точки Р от центра (центральное расстояние точки Р), r есть радиус окружности.

 

Фиг. 8а Фиг. 8б

 

Если точка Р лежит вне окружности, то степень точки также равна РТ².

β) Если даны две окружности с центрами О₁ и О₂, то точка Р имеет определенную степень по отношению к каждой из них. Если же точка Р по отношению к обеим окружностям (с радиусами r₁ и r₂) имеет одну и ту же степень, то

 

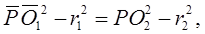
так что

 

 

следовательно, геометрическое место точек, имеющих одну и ту же степень в отношении обеих окружностей, есть (согласно h) прямая, перпендикулярная к линии центров этих окружностей; прямая мл называется радикальной осью обеих окружностей.

Если окружности пересекаются, то их радикальная ось проходит через точки их пересечения, ибо каждая из точек пересечения имеет в отношении обеих окружностей степень, равную нулю.

Если же окружности не пересекаются, то радикальную ось можно построить (фиг. 9), опустив перпендикуляр на линию центров из середины общей касательной к обеим окружностям; можно при этом следовать и другому пути, пользуясь теоремой: „Если даны на плоскости три окружности, то определяемые ими три радикальные оси проходят через одну и ту же точку (радикальный центр трех окружностей)"; доказательство теоремы основывается на том соображении, что точка пересечения двух каких-либо радикальных осей имеет одну и ту же степень в отношении всех трех окружностей, следовательно, лежит на третьей радикальной оси.

Фиг. 9

 

3. Мы разъясним метод геометрических мест на двух примерах:

а) Даны две окружности О₁, О₂ радиусов r₁ и r₂.

Требуется построить такую окружность К₁ которая касалась бы обеих данных окружностей и имела бы данный радиус r.

Если откинуть требование, чтобы окружность К касалась окружности О₂, то искомых окружностей существует бесчисленное множество; геометрическое место их центров состоит из двух концентрических с О₁ окружностей, радиусы которых соответственно равны r₁ + r и r₁ — r. Аналогично мы получим для искомого центра X и другое геометрическое место, состоящее из двух окружностей, описанных из точки О₂, как из центра, радиусами

Точка X должна совпасть с одной из точек пересечения обоих геометрических мест; существует не больше восьми точек, удовлетворяющих требованиям задачи.

β) Даны три окружности K₁, К₂, К₃; требуется построить все окружности, касающиеся трех данных (Аполлониева задача о касании).

Если (фиг. 10) через центр одной из данных трех окружностей, например, через центр окружности /С3, провести окружность, концентрическую с искомой X, то окажется, что упомянутая выше задача сведется к следующей:

Даны две окружности К΄₁, К΄₂ и точка Р΄; требуется построить окружности, касающиеся двух данных и проходящие через точку Р΄΄.

 

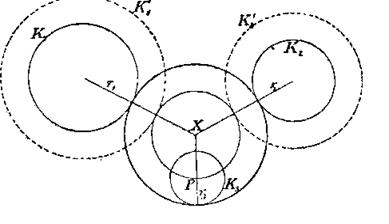
Фиг. 10

 

Геометрическое место центров всех окружностей, которые касаются окружности К₁΄΄ и проходят через точку Р, есть эллипс или гипербола, в зависимости от того, лежит ли Р внутри окружности К΄₁ или вне ее.

Центр окружности К΄₁ и точка Р являются фокусами этих конических сечений; асимптоты гиперболы перпендикулярны к касательным, которые можно провести к окружности К΄₁ из точки Р.

Каждая из данных трех окружностей может свестись и к одной точке или перейти в прямую. Геометрическое место центров окружностей, которые касаются прямой l и проходят через точку Р, есть парабола, имеющая прямую l своей директрисой, а фокус — в точке Р.

Вариант 15

 

1. Построить треугольник ΔАВС по а, с-b,

2. Построить трапецию по отношению боковых сторон, углу между ними и двум основаниям.

3. Даны прямая МN и точки A и В в одной полуплоскости относительно прямой MN. Поcтроить на прямой МN точку X такую, что

.

 

4. Вписать в данный четырехугольник параллелограмм так, чтобы его центр совпал c данной точкой.

5. В данном круге через данную внутри его точку А провести хорду так, чтобы она в точке А разделилась в отношении m : n.

6. Построить треугольник с данным отношением сторон длин биссектрисы и медианы, проведенных из одной вершины.

7. Построить прямоугольной треугольник по радиусам описанной окружности R и вписанной окружности r.

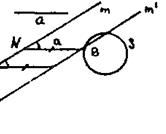
8. На приведeнных ниже чертежах дано схематичное решение четырех задач на, построение. Сформулировать эти задачи и дать их полное решение.

1)	2)
3)	4)

9. Построить ромб, зная его сторону а и отношение диагоналей р : q, где p и q заданные отрeзки. Решить задачу двумя способами.

10. Рассматриваются всевозможные треугольники c данными основанием a, угол при вершине которых равен φ. Найти множество точек пересечения медиан