Задача №3. Модель Леонтьева многоотраслевой экономики (балансовый анализ)

 

Одной из основных задач, возникающих в макроэкономике, является задача, связанная с эффективностью ведения многоотраслевого хозяйства; каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли. При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой - как потребитель продукции и своей, и произведенной другими отраслями.

Введем следующие обозначения:

 

-вектор валового выпуска;

 

х_{y -} объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства;

 

-вектор конечного продукта;

 - матрица прямых затрат, коэффициенты прямых затрат вычисляются по формуле .

 

Основная задача межотраслевого баланса - отыскание такого вектора валового выпуска , который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта .

Матричное решение данной задачи:

 

 

Работа с матрицами s пакете Excel

В пакете Excel существует несколько функций для работы с матрицами:

ТРАНСП - транспонирование матрицы;

МОПРЕД - нахождение определителя матрицы;

МУМНОЖ - умножение матриц;

МОБР - нахождение обратной матрицы.

Все эти функции (кроме ТРАНСП) находятся в категории "Математические", функция ТРАНСП - в категории "Ссылки и массивы".

Для работы с матрицами необходимо сделать следующее:

1 Выделить блок ячеек, в который нужно поместить результат.

2 Выбрать Вставка функции, найти нужную функцию.

3 Ввести адрес (или адреса) исходной матрицы (непосредственно или курсором). Нажать кнопку "ОК".

Для того, чтобы получить на экране все значения результата, нажать клавиши F2 и одновременно Ctrl+ Shift+ Enter.

Задание

Связь между тремя отраслями представлена матрицей прямых затрат А. Спрос (конечный продукт) задан вектором Y. Найти валовой выпуск продукции отраслей Х. Описать используемые формулы, представить распечатку со значениями и формулами.

Решение:

1. Вводим исходные данные в ячейки пакета Excel. Матрицу прямых затрат А вводим в ячейки (B2: D4), матрицу спроса  в ячейки (G2: G4).

 

 

2. Определим матрицу прямых затрат . Вначале найдем матрицу (Е-А).

Где Е - единичная матрица,

 

.

.

 

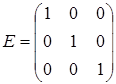Вводим в ячейки (B6: D8) единичную матрицу. Матрицу (Е-А) посчитаем в ячейках (B13: D15) по формуле

 

.

 

3. Для вычисления обратной матрицы, сначала вычислим определитель.

Для этого выставляем курсор в ячейку, где будет определитель (G14), вызываем Вставку функции, в категории "Математические" выбираем функцию нахождения определителя матрицы МОПРЕД, вводим адрес матрицы МОПРЕД (В13: D15) и нажимаем "ОК". В ячейке G14 появляется значение определителя матрицы.

 

.

 

4. Для нахождения обратной матрицы используем математическую функцию МОБР. Обратную матрицу  находим функцией МОБР:

 

.

 

Для этого выделяем блок ячеек, где должна находится обратная матрица (B17: D19), вызываем Вставку функции, в категории "Математические" выбираем функцию нахождения обратной матрицы МОБР, вводим адрес матрицы MOBP (B13: D15), нажимаем "ОК". Для получения на экране значения коэффициентов обратной матрицы, нажимаем клавиша F2 и Ctrl+Shift+Enter одновременно.

5. Вектор валового выпуска определяется по формуле , Находим вектор решений системы уравнений умножением обратной матрицы на вектор-столбец , используя встроенную математическую функцию МУМНОЖ:

 

.

 

Для этого выделяем блок, где будет находится вектор  - (G17: G19). Вызываем Вставку функции в категории "Математические", выбираем функцию МУМНОЖ, вводим адрес обратной матрицы (B17: D19) и вектора Y (G2: G4):

МУМНОЖ (B17: D19; G2: G4), нажимаем "ОК" Для получения на экране значения решения, нажимаем клавиша F2 и Ctri+ Shift+ Enter одновременно.

В результате решения было определено, что для удовлетворения спроса необходимо произвести продукции в1-й, 2-й и 3-й отраслях на 100, 100 и 90 д. е. соответственно.

 

Затраты (отрасли)	Выпуск (потребление)			Конечный продукт	Валовой выпуск
	1	2	3
1	0,05	0.15	0,4	44	100
2	0,1	0.1	0,3	53	100
3	0,3	0,15	0,2	27	90

 

	A	B	C		D	E		F	G
1	РАСЧЕТ ВАЛОВОГО ВЫПУСКА ПРОДУКЦИИ
2		0,05	0,15	0,4						44
3	А=	0,1	0,1	0,3				Y=		53
4		0,3	0,15	0,2						27
5
6		1	0	0
7	Е=	0	1	0
8		0	0	1
9
10
11	Решение задачи
12
13		0,95	-0,15	-0,4
14	E-A=	-0,1	0,9	-0,3				D=		0,50175
15		-0,3	-0,15	0,8
16
17		1,34529148	0,358744	0,807175						100
18	E-A (-1) =	0,33881415	1,275536	0,647733				(E-A) (-1) *Y=		100
19		0,56801196	0,373692	1,674141						90

 

	A	B	C	D	E	F	G
1	РАСЧЕТ ВАЛОВОГО ВЫПУСКА ПРОДУКЦИИ
2		0,05	0,15	0,4			44
3	А=	0,1	0,1	0,3		Y=	53
4		0,3	0,15	0,2			27
5
6		1	0	0
7	Е=	0	1	0
8		0	0	1
9
10
11	Решение задачи
12
13		=B6-B2	=C6-C2	=D6-D2
14	E-A=	=B7-B3	=C7-C3	=D7-D3		D=	=МОПРЕД (B13: D15)
15		=B8-B4	=C8-C4	=D8-D4
16
17		=МОБР (B13: D15)	=МОБР (B13: D15)	=МОБР (B13: D15)			=МУМНОЖ (B17: D19; G2: G4)
18	E-A (-1) =	=МОБР (B13: D15)	=МОБР (B13: D15)	=МОБР (B13: D15)		(E-A) (-1) *Y=	=МУМНОЖ (B17: D19; G2: G4)
19		=МОБР (B13: D15)	=МОБР (B13: D15)	=МОБР (B13: D15)			=МУМНОЖ (B17: D19; G2: G4)

 

Задача № 4

 

В опытном хозяйстве установили, что откорм животных возможен тогда, когда животное будет получать вещества А не менее 10 ед., вещества В - не менее 12 ед. и вещества С - не менее 4 ед. Для кормления животного используются два вида корма. В 1 кг корма первого вида содержится 2, 2 и 0 единиц питательных веществ соответственно. В 1 кг корма второго вида содержится 1, 3, 2 единицы питательных веществ соответственно. Цена 1 кг корма первого вида равна 50 д. е., корма второго вида - 60 д. е. Сколько корма каждого вида нужно расходовать ежедневно, чтобы затраты на него были минимальными?

Решение:

1. Формализация задачи.

Обозначим:

количество корма 1-го вида через x₁;

количество корма 2-го вида через x_2;

Тогда целевая функция - затраты на корм - равна:

 

z=50x₁+60x₂

 

Соотношение количества вещества А в дневном рационе не должно быть меньше 10 д. е., т.е.

 

2x₁+1x₂≥10

 

Соответственно для вещества В и вещества С

 

2x₁+3x₂≥12

0x₁+2x₂≥4

 

Так как x₁ и x₂ - количество продукта, то справедливо

 

x₁≥0

x₂≥0

 

Полученная математическая модель задачи о смесях:

 

{

z=50x₁+60x₂ (min)

2x₁+1x₂≥10

2x₁+3x₂≥12

0x₁+2x₂≥4

x₁≥0

x₂≥0

 

2. Точное (алгебраическое) решение формализованной задачи.

Поскольку граничные условия, содержащие оба аргумента, представлены тремя уравнениями, решаются две системы, каждая из которых состоит из двух уравнений с двумя неизвестными.

Система уравнений I:

 

{	2x1+1x2≥10 [1]
	0x1+2x2≥4 [2]

 

из [2] x₂=2; тогда из [1] x₁=4,Система уравнений II:

 

{	2x1+3x2≥12 [3]
	0x1+2x2≥4 [4]

 

из [4] x₂=2; тогда из [3] x₁=3,Принимаем x₁=4, x₂=2, поскольку значение x₁=3 не удовлетворяет неравенство 2x₁+1x₂≥10

3. Графическое решение формализованной задачи.

Строим область, являющуюся пересечением всех плоскостей математической модели полученной при формализации задачи (см. черт.1).

Находим градиент функции z: grad z = {50; 60}. Строим вектор с началом в т. (0; 0) и концом в точке (50; 60). Определяем зону допустимых решений. Для этого строим линии ограничений, приравнивая между собой левые и правые части уравнений и определяя значения точек пересечения линий ограничения с осями Х1 и Х2, присваивая значения равные 0:

 

2x₁+1x₂=10; x₁=0, x₂=10/x₁=5, x₂=0, 2x₁+3x₂=12; x₁=0, x₂=4/x₁=6, x₂=0

0x₁+2x₂=4; x₂=2, x₁=0, x₂₌0

 

Строим прямую, перпендикулярную вектору градиента. Передвигаем эту прямую в направлении, указанном вектором. Самая последняя точка, которую пересекает прямая, и есть точка максимума.

 

Рисунок 1 - Графическое решение формализованной задачи

 

4. Решение задачи с помощью пакета Excel.

Для решения данной задачи линейного программирования в пакете Excel воспользуемся помощью пункта меню Сервис, пункт Поиск решения.

Прежде, чем воспользоваться этой программой, введем исходные данные:

1. В ячейки C3 и D3 вводим значения точки максимума соответственно.

2. Вводим коэффициенты целевой функции 50 и 60 в ячейки C6 и D6 соответственно.

3. В ячейку F6 вводим формулу для вычисления целевой функции. Для этого вызываем Вставка функции - "Математические" - СУММПРОИЗВ и вводим ячейки C$3: D$3 и C6: D6. Формат функции; =СУММПРОИЗВ (С$3: 0$3; С6: D6).

4. В ячейки C4: D4 вводим нижние границы равные 0. Нижняя граница показывает, что переменные не отрицательные.

5. Вводим коэффициенты системы ограничений в ячейки C10: D12.

6. Вводим правые части системы ограничений в ячейки Н10: Н12.

7. В ячейку F10 вводим формулу расчета выполнения ограничений =СУММПРОИЗВ (С$3: D$3; C10: DО). Копируем эту формулу в ячейки F11, F12.

8. В ячейку I10 вводим формулу расчета неиспользованных ресурсов =H10-F10. Копиру ем эту формулу в ячейки I11, I12

После ввода исходных данных вызываем программу Поиск решения из пункта меню Сервис.

В окно Поиска решения вводим значения в ячейках:

1. Вводим $F$6 в окно "Установить целевую ячейку", выставляем ее "Равной минимальному значению".

2. В окошко "Изменяя ячейки" вводим $C$3: $D$3.

3. В окошке "Ограничения" выбираем пункт "Добавить"

"Ссылка на ячейку" - СЗ, знак - >=, "Ограничение" - С4. Появляется ограничение:

$С$3>=$С$4. Аналогично вводим:

$D$3>=$D$4;

$F$10>=$H$10;

$F$11>=$H$11;

$F$12>=$H$12

4. После этого нажимаем "Выполнить", далее Тип отчета - "Результаты".

Получаем решение в ячейках СЗ и D3 - значения переменных, в ячейках F6 - значение целевой функции, в ячейках F10: F12 - значения ограничений к в ячейках I10: I12 - разницу между исходными ресурсами и использованными.

 

	A	B	C		D	E	F	G	H	I
1			Переменные
2			X1	X2
3		Значения	4	2
4		Ниж. граница	0	0
5		Верхн. граница
6		F	50	60			320	max
7		Коэффициенты целевой ф-ции
8
9			Коэф-ты				Значение		Факт. ресурсы	Неисп. ресурсы
10	Сис-ма ограничений		2	1			10	>=	10	0
11			2	3			14	>=	12	-2
12			0	2			4	>=	4	0

 

	A	B	C	D	E	F	G	H	I
1			Переменные
2			X1	X2
3		Значения	4	2
4		Ниж. граница	0	0
5		Верхн. граница
6		F	50	60		=СУММПРОИЗВ (C3: D3; C6: D6)	max
7		Коэффициенты целевой ф-ции
8
9			Коэф-ты			Значение		Факт. ресурсы	Неисп. ресурсы
10	Сис-ма огранич		2	1		=СУММПРОИЗВ (C3: D3; C10: D10)	>=	10	=H10-F10
11			2	3		=СУММПРОИЗВ (C3: D3; C11: D11)	>=	12	=H11-F11
12			0	2		=СУММПРОИЗВ (C3: D3; C12: D12)	>=	4	=H12-F12

 

Экономический вывод

 

Для минимизации затрат при ежедневном расходе необходимо включат в рацион 4 кг первого вида и 2 кг второго вида кормов. при этом в рацион необходимо вносить:

Вещества А - 10 ед. при фактическом 10 ед.

Вещества В - 14 ед. при фактическом 12 ед.

Вещества С - 4 ед. при фактическом 4 ед.

Вещество В является недостаточным