Организация обучения математике

 с использованием квантового обучения

Организация обучения математике с использованием технологий квантового обучения зависит от того, умеют ли учащиеся пользоваться этими технологиями или еще с ними не знакомы.

Если учащиеся умеют пользоваться технологиями квантового обучения, то работа преподавателя значительно упрощается. Подготовительная часть заключается в разбиении учащихся на группы для практических занятий в соответствии с их типами доминантности мышления и подборе музыкального сопровождения занятий. На первом занятии учащиеся получают задание придумать себе, кем они станут в будущем. На протяжении изучения всей темы учащиеся играют роль этих успешных, умных и талантливых людей. К каждому занятию каждый учащийся придумывает, чем будет полезен материал, изучаемый на уроке, человеку его профессии. Каждое занятие начинается с аутотренинга под медленную и спокойную музыку в стиле барокко. Эта музыка звучит в качестве фона на всем занятии. Далее начинается первая часть занятия, которая длится 30-40 минут. В этой части занятия рассматриваются теоретические сведения и факты, составляются карты памяти изучаемого материала. Материал преподается с применением всех трех типов модальности. Затем следует небольшой перерыв, в течение которого музыка меняется на ритмичную. После перерыва учащиеся занимаются решением задач в соответствии с тематикой занятия. В течение первой части урока учащиеся работают в общей группе, а на решение задач разбиваются на группы в соответствии со своим типом доминантности мышления.

Кабинет оформляется учащимися под присмотром преподавателя. Обязательным является наличие следующих компонентов:

1) Удобные столы и стулья.

2) Комнатные растения.

3) Успокаивающий цвет мебели и штор.

4) Математические таблицы.

5) Портреты великих математиков.

6) Хлесткие цитаты или лозунги.

7) Компьютер с видеопроектором и музыкальной системой.

8) Удобное освещение.

9) Хорошая проветриваемость.

Если же учащиеся не знакомы с основами квантового обучения и не умеют применять его технологии, то помимо работы, описанной выше, перед учителем стоит еще задача обучить учащихся основным методам квантового обучения. Первые две-три карты памяти учащиеся составляют совместно с преподавателем, на последующих занятиях учащиеся составляют карты памяти сами, а преподаватель лишь выделяет ключевые моменты и факты, которые должны в карте памяти присутствовать. Обучение ведению «Записей:ФС» не требуется, учащихся следует лишь познакомить с этим типом ведения записей. Методы творческого мышления рассматриваются и отрабатываются при решении задач. В качестве примера построения системы занятий по математике можно рассмотреть систему занятий, разработанную для проведения опытной работы.

Опытная работа

В ходе исследований была проведена опытная работа. Она проводилась в Вятском государственном гуманитарном университете среди студентов 1 курса математического факультета. Среди трех учебных групп были выбраны 15 студентов, которые непосредственно приходили заниматься на данный факультатив, и 10 студентов было набрано в число опытной группы для сравнения полученных результатов. Основными целями моего исследования были:

· выявить возможность применения методов квантового обучения при обучении математике;

· разработка методики применения методов квантового обучения при обучении математике;

· оценка эффективности данной методики.

Цели, которые ставились перед факультативом:

Образовательные – обобщение и систематизация знаний школьного курса геометрии. Овладение учащимися методами квантового обучения.

Развивающие – Развитие творческой и мыслительной деятельности учащихся на уроке, развитие интеллектуальных качеств личности школьников таких, как самостоятельность, гибкость, формирование навыков коллективной и самостоятельной работы.

Воспитательные – прививать учащимся интерес к предмету посредствам необычных методов ведения урока; формировать умения выполнять математические записи.

Занятия проводились постоянно без длительных перерывов два раза в неделю по университетскому расписанию (два академических часа - одно занятие). Факультатив состоял из 16 академических часов. Темой данного факультатива были «Многогранники и круглые тела». Обусловлено это, прежде всего, составом слушателей, для которых было достаточно полезным повторение и систематизация изученных в школе геометрических тел и их свойств.

Поурочное планирование темы «Многогранники и круглые тела»:

1) Проведение тестов (определялись: уровень творческого мышления, уровень пространственного мышления, тип модальности мышления, тип доминантности мышления);

2) Квантовое обучение. Методы ведения записей; История возникновения и изучения стереометрии. Определение многогранника и геометрического тела;

3) Призма. Пирамида. Методы творческого мышления. Решение задач;

4) Правильные многогранники. Полуправильные многогранники. Построение сечений. Золотое сечение;

5) Тела вращения. Цилиндр. Решение задач;

6) Конус. Шар. Решение задач;

7) Объемы тел. Решение задач.

8) Выполнение заключительных тестов;

В качестве оценки развития творческого мышления был выбран тест Гилфорда в двух вариантах: первый – входной, второй - выходной. Данный тест направлен на изучение креативности, творческого мышления. Исследуемые факторы:

1) Беглость (легкость, продуктивность) – этот фактор характеризует беглость творческого мышления и определяется общим числом ответов.

2) Гибкость – фактор характеризует гибкость творческого мышления, способность к быстрому переключению и определяется числом классов (групп) данных ответов.

3) Оригинальность – фактор характеризует оригинальность, своеобразие творческого мышления, необычность подхода к проблеме и определяется числом редко приводимых ответов, необычным употреблением элементов, оригинальностью структуры ответа.

4) Точность – фактор, характеризующий стройность, логичность творческого мышления, выбор адекватного решения, соответствующего поставленной цели.

По результатам входного и выходного тестов проводился сравнительный анализ, позволивший сделать вывод о влиянии методов квантового обучения на уровень развития творческого мышления. В частности, по одному из факторов (гибкость мышления) были получены следующие результаты:

 

 

Занятия проводились в учебной аудитории Вятского государственного гуманитарного университета, оборудованной в соответствии с положениями квантового обучения, за исключением наглядных пособий – вместо них использовался видеопроектор.

Выводы по главе 2

Проведение опытной работы не выявило существенных преимуществ использования квантового обучения с точки зрения математических знаний и умений учащихся, уровень их творческого мышления так же повысился незначительно. Это можно объяснить небольшим сроком использования данных методов и недостатками методических разработок. С точки зрения психологии налицо возросший интерес к изучаемому предмету. Поэтому по результатам проведенных исследований можно сделать следующий вывод: идеи и методы квантового обучения можно использовать в обучении математике, и это использование будет давать положительный эффект не только в сфере математических знаний и умений учащихся, но и в контексте развития творческой личности школьника.

 

Заключение

Настоящее исследование посвящено такой проблеме теории и методики обучения математике, как возможность использования в обучении математике интенсивных методов обучения. Основным средством для решения этой проблемы было выбрано квантовое обучение.

В соответствии с поставленными целями перед данной выпускной квалификационной работой и результатами, полученными в ходе исследования, можно сделать следующие выводы:

Анализ научно-методической литературы, посвященной теоретическим аспектам квантового обучения, позволил выделить его основные методы. В результате была выработана общая схема применения данных методов.

Была разработана соответствующая методика применения методов квантового обучения в обучении математике. По результатам опытной работы можно сделать вывод о положительном влиянии разработанной методики на уровень математических знаний и умений учащихся, а так же на уровень их творческого мышления. Таким образом, опытная работа доказала, что целенаправленное и рациональное внедрение в практику новых учебных методов – методов квантового обучения ведет повышению уровня математических знаний и умений учащихся, а так же способствует развитию творческой личности школьника.

Среди перспектив работы можно выделить следующие:

а) более подробная разработка методики работы с каждым компонентом квантового обучения в процессе обучения математике;

б) доработка предложенных методов для применения в изучении алгебры и начал анализа;

в) разработка новых специализированных методов обучения математике, в основу которых легли бы методы квантового обучения;

Сделанные выводы дают основание полагать, что справедливость гипотезы исследования экспериментально подтверждена, все поставленные задачи исследования решены.

Приложения

Аутотренинг

Сядьте на стул или табурет и слегка свесьте голову вперед. Можно так же откинуться на спинку кресла, откинув голову на его спинку. Руки и кисти рук свободно лежат на бедрах. Поставьте ноги поудобнее, слегка развернув ступни носками наружу. Глаза должны быть закрытыми.

Представьте, что вы накладываете на лицо расслабляющую маску. Эта успокаивающая маска разглаживает ваши нахмуренные брови, снимает напряжение, убирает морщинки. Все мышцы лица расслабляются и освобождаются от напряжения. Ваши веки опускаются и не трепещут. Сфокусируйте взгляд на кончике носа. Челюсть расслаблена, рот слегка приоткрыт. Нижние зубы не касаются верхних. Упритесь кончиком языка в то место, где верхняя десна встречается с зубами, как будто вы собираетесь беззвучно произнести д или т.

Начните очень осторожно дышать животом, то есть дышите глубоко, но не напрягаясь. При вдохе почувствуйте, как воздух втекает в вас, наполняя легкие и заставляя живот выпячиваться. Выдыхая, почувствуйте, как живот опускается и легкие опустошаются. Дышите медленно. Выдыхайте в два раза медленнее, чем вдыхаете. С каждым вдохом удлиняйте его продолжительность, считая. Вдох: 2,3; выдох: 2,3,4,5,6. Вдох: 2,3,4; выдох: 2,3,4,5,6,7,8. Начните со вдоха на 1-2 счета, затем увеличьте его продолжительность до 6 или 7. Не напрягайтесь. Затем вернитесь к первоначальному состоянию, повторяя ту же процедуру. Вдох – на 6, выдох – на 12. Вдох – на 4, выдох на 8. И снова вдох – на 1. Проделывайте это в течение двух или трех минут.

Почувствуйте, как ваши руки становятся безвольными и тяжелыми. Они становятся все тяжелее и тяжелее. Они совершенно тяжелые. Теперь почувствуйте, как по ним разливается тепло. Они становятся все теплее и теплее. Они совершенно теплые. Почувствуйте биение своего сердца. Ощутите, что оно находится у вас в груди, в горле или в любом другом месте. Тепло с ваших рук и ног передается и груди, она ощущает приятную теплоту. Ваше сердце бьется ровно и спокойно. Вы совершенно спокойны. Ваше дыхание ровное и спокойное. Ваш живот становится мягким и теплым, вы чувствуете приятную теплоту в солнечном сплетении. Вы совершенно спокойны. Представьте, что приятный ветерок начинает овевать ваше лицо. Ваш лоб начинает чувствовать приятную прохладу. Вы совершенно спокойны.

Занятие 1.

Здравствуйте! Сегодня мы начинаем работу нашего спецкурса. Спецкурс этот будет не совсем обычным. С одной стороны мы с вами будем изучать знакомый вам еще из школы математический материал, но с другой стороны изучать мы его будем необычными методами. Начнем мы с вами со знакомства. На самом деле вы друг с другом еще не знакомы. Вы даже не знаете, как вас зовут. Сейчас мы это упущение исправим – вы придумаете, как вас зовут и какая у вас профессия. Один маленький нюанс – вы непременно эрудированный, творческий, инициативный, успешный человек, для вас нет слов: «не могу» и «это мне не по силам», а у вас есть слова «для меня не трудно», «я все могу». Давайте договоримся так – именно такими вы становитесь, проходя через эту дверь, а студенты первого курса математического факультета со всеми их страхами и неуверенностью остаются ждать вас в коридоре.

Теперь я представлюсь: Денис Анатольевич – специалист по активным методам обучения.

Сейчас давайте будем входить в роль, как говорят артисты. Займите удобное положение, закройте глаза и представьте, что вы находитесь в самом любимом вашем месте, где вы чувствуете себя наиболее комфортно, если такого места нет, то вспомните, что вы творческий человек и придумайте его.

<Проведение аутотренинга>

Постарайтесь запомнить все ваши ощущения. Перед началом каждого из занятий мы будем повторять то, что проделали сейчас.

Маленькое домашнее задание – придумайте 20 ответов на вопрос почему вам, как представителя столь интересной профессии будет полезно изучение основных многогранников и круглых тел.

Итак, начнем - сегодня мы с вами познакомимся со специальными методами ведения записей.

Карты памяти.

Главная цель, преследуемая при ведении записей, - фиксировать ключевые моменты книг, докладов, лекций и так далее. Хорошие эффективные записи помогают вспомнить детали, связанные с ключевыми моментами, понять основные концепции и увидеть взаимосвязи между ними. Последние исследования, посвященные тому, как мозг хранит и воспроизводит информацию, привели к созданию новых методов ведения записей, которые помогают повышать организованность, углублять понимание, дольше помнить информацию и оценивать с разных точек зрения. До недавнего времени полагали, что мозг обрабатывает информацию линейно, то есть в структурированной упорядоченной форме, как список. Такая точка зрения подкреплялась тем, что обе основные формы взаимосвязи между людьми – речь и письмо – являются линейными. Но это обусловлено физическими ограничениями, вследствие которых рот формирует в один момент времени только одно слово. И если мы хотим, чтобы другие нас понимали, эти слова должны следовать в определенном порядке. А не превращаться в месиво звуков. Однако сейчас ученые считают, что это всего лишь «результат», а не отражение «процесса» связи. На самом деле сам процесс, формирующий элементы линейной речи, ни в коей мере не является линейным. Для того, чтобы обеспечить словесное взаимодействие, мозг должен осуществлять одновременно поиск, сортировку, отбор, формулировку, упорядочение, организацию материала, обеспечивать взаимосвязь и придавать смысл смеси возникающих на подсознательном уровне слов и идей. В то же время эти слова переплетаются с картинками, символами, образами, звуками и чувствами. То есть на самом деле в мозгу сплетается невероятнейший клубок, но на выходе мы имеем набор последовательных слов, связанных логикой, упорядоченных грамматикой и заключающих в себе вполне четкий смысл. Это происходит в мозгу того, кто говорит. Подобное происходит и у тех, кто слушает произносимые слова. Хотя в данный момент времени человек слышит одно слово, процесс его понимания далеко не прост. Слушателям приходится анализировать каждое слово в контексте предшествующей и последующей информации. Исследования этих сложных процессов взаимосвязи привели к переосмыслению и переоценке методов написания книг, выработке подходов к эффективному обучению и способов ведения действительно полезных записей. Далее я расскажу вам о двух наиболее эффективных методах ведения записей – это «Записи: фиксирование и создание» и составление «карт памяти».

Составление карты памяти.

При составлении карты памяти используйте разноцветные ручки и начинайте с середины страницы. Если вам так удобнее, то поверните лист горизонтально, чтобы было больше места для рисунка. Затем выполните следующие операции.

1. Напишите печатными буквами в центре страницы главную тему или идею и заключите ее в круг, прямоугольник или фигуру другой формы.

2. Для каждого ключевого момента или главной идеи нарисуйте расходящиеся от центра ответвления. Количество ответвлений можно менять в зависимости от числа идей или разделов. Для каждого ответвления используйте свой цвет.

3. Для каждой ветви напишите ключевое слово или фразу, оставив место для добавления деталей. Ключевые слова должны отображать суть идеи и приводить в действие вашу память. Если вы используете различные сокращения, то вы должны быть уверены в том, что вспомните их значение через несколько дней или недель.

4. Добавляйте символы или рисунки, чтобы легче было потом вспоминать.

Эффективность восстановления информации с помощью карты памяти позволяют следующие приемы.

· Пишите разборчиво, чаще пользуйтесь заглавными и печатными буквами.

· Важные идеи пишите более крупным шрифтом, чтобы они сразу бросались в глаза при просмотре записей.

· Придавайте карте памяти личностный характер, внося свои специфические детали. Символ в виде часов может означать, что данный вопрос должен быть решен строго в срок. Некоторые используют стрелки для указания элементов, связанных определенными действиями или требующих таких действий.

· Подчеркивайте слова. Используйте жирный шрифт.

· Проявляйте творческое начало и фантазию, мозг лучше всего запоминает необычные вещи.

· Для выделения определенных элементов и идей используйте обводящие линии самой произвольной формы.

· При построении карты памяти располагайте лист бумаги горизонтально, это позволит увеличить рабочее пространство.

Теперь давайте устроим маленький перерыв, а потом приступим к изучению собственно математики.

<перерыв>

Стереометрия, или геометрия в пространстве,— это раздел геометрии, изучающий форму, размеры и свойства различных фигур и их положение в пространстве. Стереометрия — слово греческого происхождения (стереос — пространственный и метрео — измерять).

Стереометрия, как и планиметрия, возникла и развивалась в связи с потребностями практической деятельности человека. О зарождении геометрии в Древнем Египте около 2000 лет до н.э. древнегреческий ученый Геродот (V до н.э.) писал, что египетский фараон разделил землю, дав каждому египтянину участок по жребию, и взимал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и в соответствии с этим уменьшал налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию.

При строительстве даже самых примитивных сооружений необходимо было рассчитать, сколько материала пойдет на постройку, уметь вычислить расстояния между точками в пространстве и углы между прямыми и плоскостями, знать свойства простейших геометрических фигур. Так, египетские пирамиды, сооруженные за 2—3 тысячи лет до н. э., поражают точностью своих метрических соотношений, свидетельствующих, что их строители уже знали многие стереометрические положения и расчеты.

Развитие торговли и мореплавания требовало умений ориентироваться во времени и пространстве: знать сроки смены времен года, уметь определять свое местонахождение по карте, измерять расстояние и находить направление движения. Наблюдения за Солнцем, Луной, звездами и применение законов взаимного расположения прямых и плоскостей в пространстве позволили решить многие задачи небесной механики, дали начало новой науке — астрономии.

Начиная с VII в. до н. э. в Древней Греции возникают так называемые философские школы. В них все большее значение приобретают рассуждения, с помощью которых удавалось получать новые геометрические свойства. Происходит постепенный переход от наглядно-практической к теоретической геометрии.

Одной из первых и наиболее известных таких школ была Пифагорейская (VI — V до н.э.), названная так в честь своего основателя Пифагора. Вам хорошо известно это имя (в курсе планиметрии вы изучали теорему Пифагора о соотношении длин сторон прямоугольного треугольника). Философское объяснение устройства мира пифагорейцы тесно связывали с математикой. Выделяя стихии как первоосновы бытия, древние ученые приписывали их атомам форму правильных многогранников, а именно: атомам огня — форму тетраэдра (рис. 1, а), земли — гексаэдра (рис. 1, б), воздуха — октаэдра (рис. 1, в), воды — икосаэдра (рис. 1, г). Всей вселенной присваивалась форма додекаэдра (рис. 1, д).

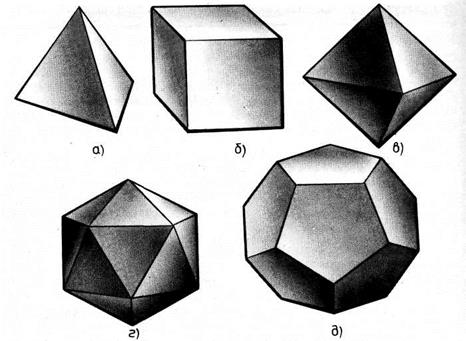
Испанский живописец Сальвадор Дали использовал этот символ в своей картине «Тайная вечеря», на которой Христос и его ученики изображены сидящими на фоне огромного прозрачного додекаэдра. Гранями додекаэдра являются правильные пятиугольники. Если стороны правильного пятиугольника продолжить до взаимного пересечения, то получится правильный звездчатый пятиугольник (рис. 2). Эта фигура, называемая также пентаграммой, была эмблемой школы Пифагора. Пентаграмме присваивалась способность защищать человека от злых духов. Вот что мы находим, читая «Фауста» Гете:

Мефистофель: Нет, трудновато выйти мне теперь, Тут кое-что мешает мне немного: Волшебный знак у вашего порога. Не пентаграмма ль этому виной?

Фауст:          Но как же, бес, пробрался ты за мной? Каким путем впросак попался?

Мефистофель: Изволили ее вы плохо начертить, И промежуток в уголку остался, Там, у дверей,— и я свободно мог вскочить.

Более поздняя философская школа — Александрийская, интересна тем, что дала миру знаменитого ученого Евклида (IV до н.э.). К сожалению, жизнь его мало известна. В одном из своих сочинений математик Папп, современник Евклида, изображает его как человека исключительно честного, тихого и скромного, которому были чужды гордость и эгоизм. Насколько серьезно и строго он относился к изучению математики, можно судить по следующему известному рассказу: царь Птолемей спросил у Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению геометрии, чем его «Начала». Евклид на это ответил: «В геометрии нет царского пути».

Славу Евклиду принесло его научное сочинение из 13 книг под общим названием «Начала», в котором впервые было представлено стройное аксиоматическое построение геометрии, т. е. сначала вводились основные неопределяемые понятия и постулировались их свойства (аксиомы), а все остальные утверждения (теоремы, следствия) выводились путем логических рассуждений из аксиом и ранее доказанных утверждений. На протяжении более двух тысячелетий «Начала» Евклида остаются основой изучения систематического курса геометрии.

В последние столетия возникли и развивались новые направления геометрических исследований: аналитическая геометрия, геометрия Лобачевского, проективная геометрия, топология и др. Появились новые методы, в том числе координатный и векторный, позволяющие переводить геометрические задачи на язык алгебры и наоборот. Геометрические методы широко используются в других науках: теории относительности, квантовой механике, кристаллографии и т. д.

Таким образом, мы вплотную подошли к определению многогранника. Но прежде, чем его дать, сначала давайте поговорим о геометрическом теле.

Геометрическое тело.

Точка М называется граничной точкой данной фигуры F , если среди сколь угодно близких к ней точек (включая ее саму) есть точки, как принадлежащие фигуре, так и не принадлежащие ей. Множество всех граничных точек фигуры называется ее границей. Так, например, границей шара является сфера.

Точка фигуры, не являющаяся граничной, называется внут ренней точкой фигуры. Каждая внутренняя точка фигуры характеризуется тем, что все достаточно близкие к ней точки пространства также принадлежат фигуре. Так, любая точка шара, не лежащая на сфере — его границе, является внутренней точкой шара.

Фигура называется ограниченной, если ее можно заключить и какую-нибудь сферу. Очевидно, что шар, тетраэдр, параллелепипед — ограниченные фигуры, а прямая и плоскость — неограниченные.

Фигура называется связной, если любые две ее точки можно соединить непрерывной линией, целиком принадлежащей данной фигуре. Примерами связных фигур являются тетраэдр (см. рис. а), параллелепипед (см. рис. б), октаэдр (см. рис. 68), плоскость. Фигура, состоящая из двух параллельных плоскостей, не является связной.

Геометрическим телом (или просто телом) называют ограниченную связную фигуру в пространстве, которая содержит все свои граничные точки, причем сколь угодно близко от любой граничной точки находятся внутренние точки фигуры. Границу тела называют также его поверхностью и говорят, что поверхность ограничивает тело.

Плоскость, по обе стороны от которой имеются точки данного тела, называется секущей плоскостью. Фигура, которая образуется при пересечении тела плоскостью (т. е. общая часть тела и секущей плоскости), называется сечением тела.

Теперь перейдем е определению многогранника. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником. Тетраэдр и параллелепипед — примеры многогранников. На рисунке а) изображен еще один многогранник — октаэдр. Он составлен из восьми треугольников. Тело, ограниченное многогранником, часто также называют многогранником.

Многоугольники, из которых составлен многогранник, называются его гранями. Гранями тетраэдра и октаэдра являются треугольники, гранями параллелепипеда — параллелограммы. Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

 

 

Многогранники бывают выпуклые и невыпуклые. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Тетраэдр, параллелепипед и октаэдр — выпуклые многогранники. На рисунке изображен невыпуклый многогранник, составленный из восьми многоугольников.

Ясно, что все грани выпуклого многогранника являются выпуклыми многоугольниками. Можно доказать, что в выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360°. Рисунок 70 поясняет это утверждение: многогранник «разрезан» вдоль ребер и все его грани с общей вершиной А развернуты так, что оказались расположенными в одной плоскости а. Видно, что сумма всех плоских углов при вершине А, т. е. .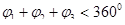

 

На этом мы закончим наше сегодняшнее занятие, жду всех вас на следующем.

< Повторное проведение аутотренинга, музыка в конце сменяется на ритмичную>

 

Занятие 2

<аутотренинг>

Призма.

Рассмотрим два равных многоугольника и A₁A₂…A_n и B₁B₂…B_n расположенных в параллельных плоскостях α и β так, что отрезки А₁В₁, А₂В₂, ..., А_пВ_п, соединяющие соответственные вершины многоугольников, параллельны (рис.71).

Каждый из п четырехугольников A₁A ₂ B ₂ B₁, A₂A₃B₃B₂,…, A_nА₁B₁B_n является параллелограммом, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике A₁A ₂ B ₂ B₁ стороны А₁В₁и А₂В₂ параллельны по условию, а стороны А₁А₂и В₁В₂— по свойству параллельных плоскостей, пересеченных третьей плоскостью.

Многогранник, составленный из двух равных многоугольников A₁A₂... A_n и В₁В₂...В_п, расположенных в параллельных плоскостях, и п параллелограммов, называется призмой (см. рис. 71).

Многоугольники A₁A₂…A_n и B₁B₂…B_n называются основания ми, а параллелограммы — боковыми гранями призмы. Отрезки А₁В₁ А₂В₂, ..., А_пВ_п называются боковыми ребрами призмы. Эти ребра как противоположные стороны параллелограммов, последовательно приложенных друг к другу, равны и параллельны. Призму с основаниями A₁A₂…A_n и B₁B₂…B_n обозначают А₁А₂...A_nB ₁ B ₂ ... B_n и называют п-угольной призмой. На рисунке 72 изображены треугольная и шестиугольная призмы, а на рисунке 1 б — четырехугольная призма, т. е. параллелепипед.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, впротивном случае — наклонной. Высота прямой призмы равна еебоковому ребру.

Прямая призма называется правильной, если ее основания — правильные многоугольники. У такой призмы все боковые грани — равные прямоугольники. На рисунке 72 изображена правильная шестиугольная призма.

Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности приз мы — сумма площадей ее боковых граней. Площадь 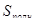 полной поверхности выражается через площадь  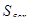боковой поверхности и площадь S_0CH основания призмы формулой:

.

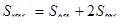Докажем теорему о площади боковой поверхности прямой призмы.

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Доказательство. Боковые грани прямой призмы — прямоугольники, основания которых — стороны основания призмы, а высоты равны высоте h призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т. е. равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, т. е. его периметр Р. Итак, S _{6 o к} = Ph . Теорема доказана.

Пирамида.

Рассмотрим многоугольник A ₁ A ₂ ... A_n и точку Р, не лежащую в плоскости этого многоугольника. Соединив точку Р отрезками с вершинами многоугольника, получим п треугольников (рис. 73): РА₁А₂,, РА₂А₃,, ..., РА_пА₁.

Многогранник, составленный из п-угольника А₁А₂...А_п и п треугольников, называется пирамидой. Многоугольник A ₁ A ₂ ... A_n называется основанием, а треугольники — боковыми гранями пирамиды. Точка Р называется вершиной пирамиды, а отрезки РА₁,, РА₂,, ..., РА_п — ее боковыми ребрами. Пирамиду с основанием A ₁ A ₂ ... A_n и вершиной Р обозначают так: Р A ₁ A ₂ ... A_n — и называют n-угольной пирамидой. На рисунке 74 изображены четырехугольная и шестиугольная пирамиды. Ясно, что треугольная пирамида — это тетраэдр.

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 73 отрезок РН — высота пирамиды.

Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды — сумма площадей ее боковых граней. Очевидно,

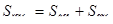
Правильная пирамида.Пирамида называется правильной, если ее основание — правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой (рис. 75).

Докажем, что все боковые ребра правильной пирамиды рав ны, а боковые грани являются равными равнобедренными треугольниками.

Рассмотрим правильную пирамиду РА₁А₂...А_п (рис. 75). Сначала докажем, что все боковые ребра этой пирамиды равны. Любое боковое ребро представляет собой гипотенузу прямоугольного треугольника, одним катетом которого служит высота РО пирамиды, а другим — радиус описанной около основания окружности (например, боковое ребро РА₁— гипотенуза треугольника ОРА₁в котором OP = h , OA₁ = R ). По теореме Пифагора любое боковое ребро равно 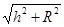, поэтому РА₁=РА₂ = ... = РА_п.

Мы доказали, что боковые ребра правильной пирамиды РА₁А₂...А_п равны друг другу, поэтому боковые грани — равнобедренные треугольники.

Основания этих треугольников также равны друг другу, так как A ₁ A ₂ ... A_n — правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников, что и требовалось доказать.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. На рисунке 75 отрезок РЕ — одна из апофем. Ясно, что все апофемы правильной пирамиды равны друг другу.

Докажем теорему о площади боковой поверхности правильной пирамиды.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Доказательство. Боковые грани правильной пирамиды — равные равнобедренные треугольники, основания которых — стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой поверхности пирамиды равна сумме произведении сторон основания на половину апофемы d . Вынося множитель 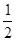d за скобки, получим в скобках сумму сторон основания пирамиды, т. е. его периметр. Теорема доказана.

Усеченная пирамида.Возьмем произвольную пирамиду РА₁А₂...А_п и проведем секущую плоскость β, параллельную плоскости α основания пирамиды и пересекающую боковые ребра в точках В₁, В₂,,.... В_п (рис. 76). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются п-угольники А₁А₂...А_п и В₁В₂...В_п (нижнее и верхнее основания), расположенные в параллельных плоскостях, и п четырехугольников A₁A ₂ B ₂ B₁, A₂A ₃ B ₃ B₂,…, А_пА₁В₁В_п (боковые грани), называется усеченной пирамидой. Отрезки А₁В₁, А₂В₂, ..., А_пВ_п называются боковыми ребрами усеченной пирамиды.

Усеченную пирамиду с основаниями А₁А₂...А_п и В₁В₂...В_п обозначают так: А