Построение нагрузочной диаграммы скорости как функции угла поворота кривошипа

Описание исполнительного механизма и технологического процесса его работы

 

В данном курсовом проекте рассматривается расчет привода подъёмно-качающегося стола. Стол предназначен для передачи слитка с одного ручья прокатного стана на другой. Слитки на стол подаются рольгангом в нижнем положении и снимаются с него в верхнем положениях. В исходное положение (нижнее) стол возвращается без слитка. Двигатель выключается до следующего поступления слитка на стол.

 

Задание на курсовое проектирование

Кинематический анализ механизма

 

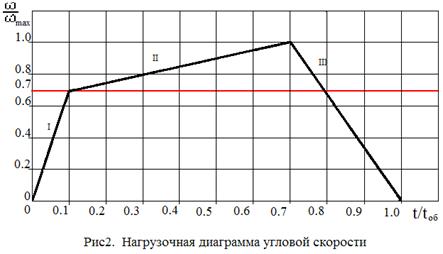
Рассчитать привод подъёмно-качающегося стола, схема которого приведена на рис. 1, нагрузочная диаграмма угловой скорости на рис. 2

 

Рис. 1. Кинематическая схема подъёмно-качающегося стола:

1 - слиток; 2 - стол; 3 - штанга; 4 - трёхплечий рычаг;

5 - контргруз; 6 -шатун; 7 - кривошип; 8 - редуктор.

 

 

 

В таблице 1 приведены значения параметров для варианта 1.

 

Таблица 1

1	Вес слитка, кН, Gсл	30
2	Вес стола, кН, Gст	800
3	Вес контргруза, кН, Gгр	208
4	Длина слитка, м, Lсл	2,4
5	Расстояние ОзА, м, Lа	8,2
6	Длина стола, м, Lст	10
7	Радиус кривошипа, м, rкр	0,35
8	Длина шатуна, м, Lш	3,0
9	Радиус 1 го рычага, м, rl	0,65
10	Радиус 2 го рычага, м, r2	0,7
11	Радиус 3 го рычага, м, r3	1,7
12	Угол наклона рычагов к горизонту, град, γ	5
13	Число циклов в час, 1/ч, Z	170
14	Время работы, с, toб	8,4
15	Угловая скорость двигателя, рад/с, ωдв	75

 

По нагрузочной диаграмме угловой скорости (рис. 2) определим:

значение угловой скорости ω_max;

зависимость угловой скорости от угла поворота φ кривошипа;

вычислим передаточное число редуктора.

Разобьем нагрузочную диаграмму на участки I, II, III.

Участок I

Время изменяется в пределах

движение равноускоренное, угол поворота определим по формуле

,                                                        (1)

где:

ε _I – угловое ускорение рад/с.,

t – время в с.,

φ – угол поворота.

ε _I -находим из условия, что к моменту 0.1t, ω _I = 0.7ω _max, Так как в начальный момент ω = 0 поэтому ω = ε t , следовательно

                                     (2)

Уравнение вращательного движения на I участке примет вид

                                                          (3)

Угол поворота φ на участке I к моменту 0.1t_{o б}

                   (4)

Из выражения (3) выразим t.

,                                                                      (5)

подставим в выражение (1) уравнение движения (5) и закон изменения угловой скорости (2), получаем

                     (6)

Отсюда:

                                                            (7)

Участок II

Время изменяется в пределах

,

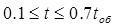движение равноускоренное, угловое ускорение определим по формуле

.                                       (8)

Где:

∆ω – изменение скорости за весь второй участок

1 ω _max - 0,7 ω _max = 0,3ω _max;

∆ t – изменение времени за весь второй участок

0,7t_{o б} - 0,1t_{o б} = 0,6t_{o б}.

Уравнение вращательного движения на этом участке

φ = φ_о + ω_о (t-t_o)+ ε (t-t_o)² /2

φ_о– угол поворота в начале участка II(конец участка I),

t_o– начальный момент времени для участка II,

ω_о– скорость вращения в начале участка II.

Подставляя все значения, получаем

φ = 0,035 ω _max t_{o б} +0,7 ω _max ( t - 0,1 t_{o б} )+ 0,5 ω _max ( t - 0,1 t_{o б} )²/2 t_{o б} (9)

Выражение (9)

при t =0,1 t_{o б} (начало участка II ) даетзначение φ = 0,035ω _maxt_{o б}

при t =0,7 t_{o б} (конец участка II ) дает значение φ = 0,545 ω _maxt_{o б}

Закон изменения скорости на участке II примет вид

                                                                                         (10)

Подставим значение ω ₀ =0,7 ω _max и 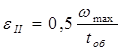 получим

(11)

Отсюда . Значение t подставим в выражение (9)

Из этого выражения выразим ω _II

                               (14)

Участок III

Время изменяется в пределах

,

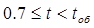Так как движение равнозамедленное, отрицательное угловое ускорение определим по формуле

.                                      (15)

Где:

∆ω – изменение скорости за весь третий участок            ∆ω = ω _max;

∆ t – изменение времени за весь третий участок ∆ t = 1 - 0,7 t_{o б} .= 0,3 t_{o б}

Закон изменения скорости на участке III примет вид

                                                                                               (16)

Уравнение вращательного движения на этом участке

φ = φ_о + ω_о (t-t_o)+ ε _III (t-t_o)² /2

φ_о– угол поворота в начале участка III(конец участка II), φ = 0,545 ω _max t_{o б}

t_o– начальный момент времени для участка III, t_o = 0,7 t_{o б}

ω_о– скорость вращения в начале участка III- ω_о= ω _max.

Подставляя все значения, получаем

φ = 0,545 ω _max t_{o б} + ω _max ( t - 0,7 t_{o б} ) - ω _max ( t - 0,7 t_{o б} )²/0,6 t_{o б}       (17)

Выражение (17)

при t = 0,7 t_{o б} (начало участка III ) даетзначение φ = 0,545 ω _max t_{o б}

при t = t_{o б} (конец участка III ) дает значение

φ = 0,545 ω _max t_{o б} + 0,3 ω _max t_{o б} - ω _max (0,09 t_{o б} ² )/0,6 t_{o б} =0,695ω_max t_{o б}

Из выражения (16) выразим t

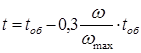,                                                                                                           (18)

и подставим в выражение (17). Преобразовывая, получим.

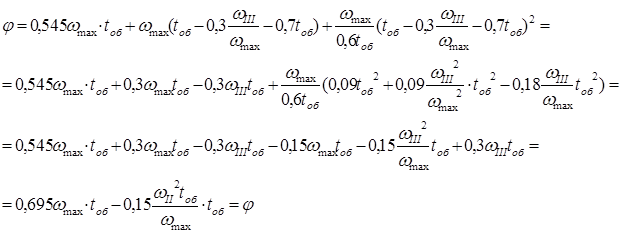
Из этого выражения выразим ω _III

              (18)

Значение ω_max определим из выражения (17) при t = t_{o б} (конец участка III ) φ =0,695ω_max t_{o б} . Полный оборот φ = 2π выходной вал редуктораделает за t_{o б} =8,4с , поэтому ω_max = 2π/0,695 t_{o б} = 1,05рад/с

Передаточное число редуктора:

Где:

ω _дв = 75-угловая скорость быстроходного вала редуктора, рад/с;

ω _max = 1,05-угловая скорость тихоходного (ведомого) вала редуктора, рад/с.

 

Построение нагрузочной диаграммы скорости как функции угла поворота кривошипа

 

По результатам расчётов угловой скорости и углового ускорения кривошипа строим графики ω = ω (φ) рис.1. и ε = ε (φ) рис.2. приложения 1

Диаграммы строим по результатам кинематического расчёта для двенадцати положений механизма через 30^О и дополнительно включая точки перелома соответствующие углам поворота для t =0,1 t_{o б} рассчитываем по формуле (4) т.е.

φ = 0,035 ω _max t_{o б} = 0,035 * 1,05 * 8,4 = 0,309 рад=180*0,309 /π=18^О

и для t =0,7 t_{o б} рассчитываем по формуле (9) т.е.

φ = 0,545 ω _max t_{o б} =0,545*1,05*8,4 =4,807 рад = 180*4,807 /π=276 ^О

Для уточнения вида диаграммы на участке I найдем ω и ε на углах поворота φ = 6 ^О и 12 ^О .

ε и ω рассчитываем следующим образом:

при 0^О ≤ φ ≤ 18^О расчет ведем по выражениям (2)и (7) соответственно;

при 18^О < φ ≤276 ^О расчет ведем по выражениям (8)и (14) соответственно;

при 276 ^О < φ < 360^О расчет ведем по выражениям (15)и(20) соответственно.

Результаты рассчитанные в программе Mathcad 12 (приложение 1) сведены в таблицу 2.

3 Построение планов скоростей

 

Планы скоростей строятся для двенадцати положений механизма. С помощью планов скоростей определяются скорости всех характерных точек механизма и центров весомых звеньев. Планы скоростей в приложении 2.

Рассматривая движение кривошипа, находим скорость точки А. Модуль скорости точки А определяется выражением

.

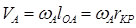Вектор V _A скорости точки А направлен в сторону вращения кривошипа перпендикулярно этому звену. На плане скоростей вектор отображается в выбранном масштабе отрезком [ра].

Рассматривая движение шатуна АВ как плоское и выбирая за полюс точку А, находим скорость точки В

V_В = V_А+ V_ВА.

При этом векторном уравнении неизвестны лишь модули векторов V_А и V_ВА (здесь V_ВА - скорость точки В во вращательном движении звена ВА вокруг полюса А), следовательно, это уравнение можно решить графически.

Отложив в масштабе вектор V_А([ра] перпендикулярен ОА), через конец этого вектора проведём прямую, перпендикулярную шатуну АВ. Из точки р проводим прямую, перпендикулярную звену Q B в пересечении этих прямых получим точку В. Длины отрезков [рв] и [ав] в масштабе плана скоростей отражают скорость точки В – V_В и скорость точки В вокруг точки А - V_ВА соответственно.

Очевидно, .

Скорости точек С и Е отображаются на плане скоростей отрезками [рс] и [ре] соответственно и могут быть найдены аналогично предыдущему, то есть

.

Направлены V_С и V_Е перпендикулярно положению плеч r₂ и r₃ соответственно.

Скорость V_D точки D определяем графически. Для этого через точку С проводим перпендикуляр положению штанги С D. Через точку Р проводим перпендикуляр к положению стола, точка пересечения прямых есть точка D.

Угловая скорость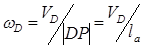          

Скорость V_F центра масс стола (точка F) и величина угловой скорости ω_F стола определяются:

V_F = ω_D | PF | где | PF |=¹/₂ L_ст

Модуль скорости Vk центра масс слитка (при условии, что толщиной слитка по сравнению с размерами стола можно пренебречьи слиток находится на краю стола без свисания) определяется аналогично

V _К = ω_D | P К| где | P К|= L_ст- L_сл/2

В результате построения планов скоростей для 1,2,3,4,5,6,7,8,9,10,10_а,11,12 положений механизма рассчитываем скорости точек и угловые скорости стола, трёхплечего рычага и шатуна. Рассчеты проведены в программе Mathcad 12 (приложение 2) Результаты сводим в таблицу 3.

Таблица 3

№ точки	VЕ м /с	VF м /с	Vk м /с	ωD рад /с	Мст кНм	J пр*103 к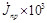гм2	кгм2	Мд кНм	М ∑ кНм	ε-2 рад/с-2	ω-1 рад/с	φ рад,с
1	0	0	0	0	0	0	-0,042	0,000	0,000	0,875	0	0
2	0,451	0,095	0,166	0,019	-10,940	9,489	22,945	9,237	-1,703	0,063	0,753	0,524
3	0,673	0,152	0,268	0,030	-8,652	19,420	15,573	7,414	-1,238	0,063	0,795	1,047
4	0,764	0,189	0,333	0,038	1,129	23,880	0,000	1,504	2,633	0,063	0,835	1,571
5	0,732	0,171	0,300	0,034	10,130	19,350	-21,415	-8,139	1,991	0,063	0,874	2,094
6	0,432	0,091	0,161	0,180	3,888	5,940	-18,321	-7,962	-4,074	0,063	0,910	2,618
7	0	0	0	0	0	0	0,	0,145	0,145	0,063	0,946	3,142
8	0,458	0,104	-	0,021	-3,752	5,881	19,937	9,647	5,895	0,063	0,980	3,665
9	0,785	0,192	-	0,038	-4,074	16,560	15,725	9,008	4,934	0,063	1,013	4,189
10	0,956	0,237	-	0,047	7,915	23,300	9,699	6,531	14,446	0,063	1,044	4,712
10а	0,961	0,239	-	0,048	9,311	23,630	3,143	-8,210	1,101	-0,417	1,046	4,817
11	0,785	0,188	-	0,038	14,900	22,820	-17,252	-16,960	-2,060	-0,417	0,863	5,236
12	0,307	0,069	-	0,014	12,930	8,220	-23,403	-9,922	3,008	-0,417	0,555	5,760

Расчёт моментов