Формулировка метода конечных элементов

По способу получения основных, т. е. разрешающих, уравнений различают четыре основных вида метода конечных элементов: прямой, вариационный, взвешенных невязок и энергетического баланса. Из приведенных видов МКЭ в строительной механике особенно актуальны вариационный метод и метод взвешенных невязок Галеркина.

Рассмотрим Вариационный метод. Данный метод основан на принципах стационарности некоторой переменной, зависящей от одной или нескольких функций (такая переменная носит название функционала). Применительно к механике деформируемого твердого тела эта переменная представляет собой потенциальную (функционал Лагранжа) или дополнительную (функционал Кастилиано) энергию системы или формируется на основе этих двух энергий (функционалы Хеллингера-Рейсснера, Ху-Вашицу). Если в функционал подставить аппроксимирующие выражения искомых функций и применить к нему экстремальные принципы (соответственно принцип Лагранжа, принцип Кастилиано и т. д.), получим систему алгебраических уравнений, решением которой будут значения узловых неизвестных.

Вариационный принцип Лагранжа: Потенциальная энергия приобретает стационарные значения на тех кинематическе возможных перемещениях, которые удовлетворяют заданным граничным условиям и условиям равновесия сил.

В отличие от прямого вариационный метод может одинаково успешно применяться как к простым, так и сложным задачам.

И так, рассмотрим трехмерный объект произвольной формы, находящийся в равновесном состоянии под воздействием некоторой нагрузки (рис. 4.1). Силы трения, действующие на поверхность (Поверхностные силы), обозначим - p, массовые силы (объемные силы) – G. В общем случае эти силы раскладываются на компоненты, параллельные осям координат:

                                              G= , p= . (1)

Рис. 4.1. Трехмерный объект с внешними силами

Обозначим смещение произвольной точки объекта (X,Y,Z) по сравнению с конфигурацией в отсутствие нагрузки символом U. Тогда

U^T=[U(X,Y,Z) V(X,Y,Z) W(X,Y,Z)]. (2)

Смещения U приведут к возникновению деформации

ε^T=[ ε_XX ε_YY ε_ZZ ε_XY ε_YZ ε_ZX ] (3)

и соответствующих напряжений

σ^T=[ σ_X σ_Y σ_Z τ_XY τ _YZ τ _ZX ]. (4)

Необходимо рассчитать U, ε, σ в точке (X,Y,Z) по заданным внешним силам. Выражение для полной потенциальной энергии упругого тела описывается выражением:

Э - энергия деформации;

А - работа приложенных массовых и поверхностных сил.

Три последних слагаемых уравнения (5) описывают внешнюю работу, выпол­няемую реальными силами G,p на виртуальных перемещениях .

Верхний индекс S у вектора  означает виртуальное смещение на поверхности.  Напряжения вычисляются через деформации по соответствующим материальным уравнениям. 

Получим из уравнения (5) уравнения метода конеч­ных элементов. Начнем с аппроксимации объекта, изображенного на рис. 4.1, сеткой конечных элементов. Элементы соединяются друг с другом в узловых точках, которые находятся на их границах. Смещение в любой точке с координа­тами ( x , y , z ) в локальной системе координат элемента считается функцией сме­щений в узловых точках.

То есть для элемента т высказывается предположе­ние, что

где H — интерполяционная матрица смещений (функций формы), а  — вектор смещений на всех узлах. Если общее количество узлов равно N вектор  запишется следую­щим образом:

Это выражение можно переписать так:

 Хотя в уравнении (8) перечисляются смещения всех узлов, а, следовательно, эти смещения входят и в выражение (6), для каждого конкретного элемента смещения внутри него определяются только смещениями в его собственных уз­лах. В уравнение же (6) все узлы вошли потому, что это облегчает процесс объ­единения матриц отдельных элементов в матрицу структуры в целом, как будет показано ниже.

Уравнение (6) позволяет вычислить деформации:

Строки матрицы деформаций-смещений  из уравнения (9) получаются дифференцированием и объединением строк матрицы H ^{( m )}.

Теперь мы можем записать и выражения для напряжений внутри каждого эле­мента:

где C — матрица упругости элемента т (матрица Гука), а  — начальное напряжение внут­ри элемента. В структуре, состоящей из разных материалов, для каждого элемента можно за­дать свою собственную матрицу упругости.

Перепишем уравнение (5) в виде суммы интегра­лов по объемам и поверхностям отдельных элементов:

где т изменяется от 1 до полного количества элементов в системе.

Подстановка (6), (9) и (10) в (11) даст следующее вы­ражение:

где поверхностные интерполяционные матрицы смещений  получаются из объемных интерполяционных матриц смещений 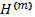 подстановкой координат поверхности элемента.

Обозначим

R = R _В + R_S - R_o ;                                  (14)

Минимизация энергии П приводит к уравнению:

которое с учетов введенных обозначений запишется так:

KU = R,    (19)

Обратите внимание, что суммирование интегралов по объемам отдельных эле­ментов в формуле (14) выражает тот факт, что матрица жесткости набора эле­ментов как целого получается сложением матриц жесткости элементов K ^{( m )}. Аналогичным образом, вектор R _в объемной силы, действующей на все тело, по­лучается суммированием векторов объемных сил, действующих на отдельные элементы. Тем же путем вычисляются и векторы прочих сил.

Выражение (19) описывает статическое равновесие. Если приложенные силы изменяются во времени, это выражение применимо к любому конкретному мо­менту. Однако при быстром приложении нагрузки необходимо учитывать силы инерции. По принципу Даламбера силы инерции отдельных элементов могут быть добавлены к массовым силам. Если предположить, что ускорение в любой точке элемента связано с ускорениями в узловых точках матрицей H ^{( m )} подобно смещениям, вклад массовых сил в вектор нагрузки К будет выражаться так:

где  — ускорения узловых точек, а  — массовая плотность элемента т.

Подстановка (20) вместо (15) в (19) дает новое уравнение равновесия:

M + KU=R,      (21)

где М — матрица масс.

Обратите внимание, что U и R в уравнении (21) являются функциями време­ни.

Демпфирующие силы могут быть учтены как дополнительный вклад в массовые силы, что позволяет описать эффект демпфирования (затухания). Уравне­ние (20) при этом принимает новый вид:

где  — вектор скоростей узловых точек, а  — демпфирующий коэффициент для элемента т.

Уравнение равновесия приобретает вид

M + C + KU=R, (23)

где С — матрица демпфирования.

На практике матрицу С обычно конструируют из массовой матрицы и матрицы жесткости на основании экспериментальных данных по демпфированию в мате­риале, потому что определить параметры демпфирования отдельных элементов достаточно сложно.