Найти производные dy / dx , пользуясь правилами и формулами дифференцирования

 

Решение:

 

а)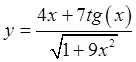

 

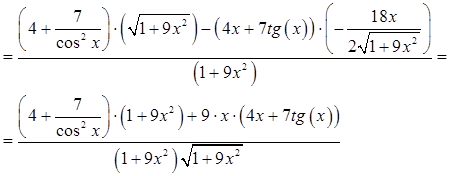
Ответ:

 

б)

 

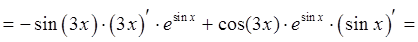
Ответ: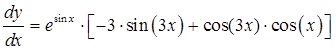

 

в)

 

 

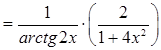
Ответ:

 

Задача 6

 

Исследовать заданные функции методами дифференциального исчисления, начертить их графики.

а) ; б)

Решение

 

а)

 

1) Областью определения данной функции являются все действительные значения аргумента х, то есть D(y) = {х: хÎ(-¥, +¥)}, а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.

2) Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:

 

Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки первого рода х₁ = 1, х₂ = 2.

Разбиваем область определения этими точками на части и по изменению в них знака производной функции выявляем промежутки ее монотонности и наличие экстремумов:

 

х	(-¥; 1)	1	(1; 2)	2	(2; ¥)
f ’(x)	+	0	-	0	+
f(x)		max		min

 

 

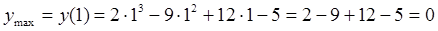
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

 

 

Итак, функция имеет одну критическую точку второго рода х = -1,5. Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:

 

х	(-¥; 1,5)	1,5	(1,5; ¥)
f ‘’(x)	-	0	+
f(x)	Ç	т. п.	È

 

Значение х = 1,5 является абсциссой точки перегиба графика функции, а ордината этой точки:

 

4) Выясним наличие у графика заданной функции асимптот. Для определения параметров уравнения асимптоты y = kx – b воспользуемся формулами

 

 

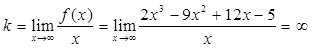
Таким образом, у графика заданной функции наклонных асимптот нет.

5) построим график функции

 

 

б)

 

1) Областью определения данной функции являются значения аргумента х

D(y) = хÎ(-¥, 0) È (0, +¥).

 

2) Исследование на непрерывность и классификация точек разрыва

Заданная функция непрерывна всюду, кроме точки х = 0. Вычислим ее односторонние пределы в этой точке:

 

 

Итак точка х = 0 – точка разрыва второго рода, а прямая х = 0 – вертикальная асимптота.

3) Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:

 

 

Следовательно, функция не имеет критических точек первого рода.

Так как y’ < 0 для всех х, то функция убывает во всей области определения

4) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

 

 

Итак функция не имеет точек перегиба. Разобьем область определения точкой х = 1 в каждой из которых установим знак второй производной:

 

х	(-¥; 0)	0	(0; ¥)
f ‘’(x)	-	не существует	+
f(x)	Ç	не существует	È

 

5) Выясним наличие у графика заданной функции асимптот. Для определения параметров уравнения асимптоты y = kx + b воспользуемся формулами

 

 

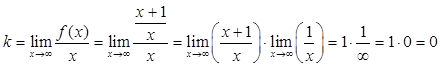
Таким образом, у графика заданной функции есть наклонная асимптота

 

y = 0*x + 1 = 1.

 

6) построим график функции