Крылатое представление ( Winged – Edge Representation).

Часто используется в компьютерной графике для распознавания объектов. Структура основывается на списке ребер, и для каждого ребра, которое мы рисуем, возникают две соседние грани. Каждое ребро ссылается на соседние грани, на ближайшие соседние ребра и опирается на две вершины. В результате ссылки для каждого ребра образуют кольцевые списки.

При описании трёхмерных моделей в качестве базовых примитивов используются точки, ребра, полигоны. Для их описания требуется задавать атрибуты и реализовывать стандартные операции:

1. Точка задается такими параметрами и методами:

- координаты x, y, z;

 - операция определения положения точки относительно заданного отрезка прямой линии (на прямой или нет, если на прямой, то на отрезке, позади или впереди отрезка и т.п.);

 - вычисление расстояния от точки до линии;

- функции вычисления полярного угла и длины;

2. Отрезок описывается такими параметрами и методами:

- две концевых точки;

- направление;

- поворот, перенос, масштабирование, отражение ребра;

- функция определения точки пересечения двух ребер;

- вычисление расстояния от точки до прямой линии;

3. Полигон - замкнутая кривая на плоскости, образуемая отрезками прямых линий. Отрезки называются ребрами, или сторонами, полигона, концевые точки отрезков - вершинами. Для представления полигонов используются различные подходы и методы.

Полигон простой, если он не пересекает сам себя. Простой полигон охватывает непрерывную область плоскости, которая называется внутренней частью полигона, оставшаяся область называется внешней. Набор точек, лежащих на самом полигоне образует границу.

Полигональные модели являются наиболее широко применяемым семейством геометрических моделей, что вызвано в первую очередь простотой их обработки на аппаратном уровне.

НАЗАД

10. Геометрические преобразования. Линейные преобразования.

Вывод изображения на экран дисплея и разнообразные действия с ним, в том числе и визуальный анализ, требуют от пользователя известной геометрической грамотности. Геометрические понятия, формулы и факты, относящиеся прежде всего к плоскому и трехмерному случаям, играют в задачах компьютерной графики особую роль. Геометрические соображения, подходы и идеи в соединении с постоянно расширяющимися возможностями вычислительной техники являются неиссякаемым источником существенных продвижений на пути развития компьютерной графики, ее эффективного использования в научных и иных исследованиях. Порой даже самые простые геометрические методики обеспечивают заметные продвижения на отдельных этапах решения большой графической задачи.

Для решения таких задач, как движение объектов и их частей, управления камерой применяются аффинные преобразования (АП), рассмотрим их основные свойства:

1) точки, лежащие на одной прямой, после преобразования лежат на одной прямой;

2) пересекающиеся прямые остаются пересекающимися, а параллельные – параллельными;

3) при АП пространства пересекающиеся плоскости остаются пересекающимися, параллельные – параллельными, а скрещивающиеся – скрещивающимися;

4) при АП сохраняются отношения площадей двух квадратов на плоскости и отношение объемов двух кубов в пространстве.

Допустим, на плоскости задана прямолинейная координатная система. Тогда каждой точке М соответствует упорядоченная пара чисел (х, у) ее координат. Вводя на плоскости ещё одну прямолинейную систему координат, мы ставим в соответствие той же точке М другую пару чисел – (x*, y*).

Переход от одной прямолинейной координатной системы на ос плоскости к другой описывается следующими соотношениями:

       Где показатели – произвольные числа, связанные неравенством

       Либо сохраняется точка и изменяется координатная система, либо изменяется точка и сохраняется координатная система.

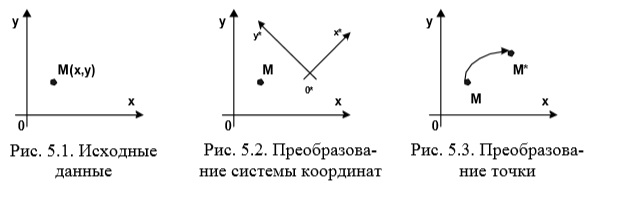
В преобразованиях плоскости особую роль играют несколько важных частных случаев, имеющих хорошо прослеживаемые геометрические характеристики.

1. Поворот вокруг начальной точки на угол ϕ описывается формулами

2. Растяжение (сжатие) вдоль координатных осей можно задать так:

3. Отражение (относительно оси абсцисс) задаётся при помощи формул

4. Параллельный перенос обеспечивают соотношения

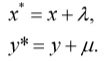
       Выбор этих четырёх частных случаев определяется двумя обстоятельствами.

1. Каждое из приведённых выше преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наделены и постоянные числа, входящие в приведённые формулы).

2. Любое преобразование вида (1) всегда можно представить как последовательное исполнение простейших преобразований.

Для эффективного использования этих известных формул в задачах компьютерной графики более удобной является их матричная запись.

НАЗАД

11. Аффинные преобразования в пространстве. Использование матричного представления. Составные аффинные преобразования в пространстве.

Обратимся к трехмерному случаю (3D) (3-dimension) и начнем рассмотрение сразу с введения однородных координат.

Поступая аналогично тому, как это было сделано в двухмерном случае, заменим координатную тройку (х, у, z), задающую точку в пространстве, на четверку чисел (x, y, z, 1) или, более общо, на четверку (hx, hy, hz),h≠0

Каждая точка пространства (кроме начальной точки О) может быть задана четверкой одновременно неравных нулю чисел; эта четверка чисел определена однозначно с точностью до общего множителя.

Предложенный переход к новому способу задания точек дает возможность воспользоваться матричной записью и в более сложных трехмерных задачах.

Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции поворотов, растяжений, отражений и переносов.

1. Матрицы вращения в пространстве:

2. Матрица сжатия (растяжения):

3. Матрицы отражения:

4. Матрицы переноса (значения здесь – координаты переноса):

Таким образом, любое сложное аффинное преобразование может быть достаточно просто получено путём комбинации четырёх базовых преобразований.

НАЗАД

12. Последовательные преобразования при обработке вершин. Модельное преобразование. Иерархия преобразований.

Модельное преобразование – из локальных в мировые координаты

Переводит модель, заданную в локальных (собственных) координатах, в глобальное (мировое пространство)

Модель «собирается» из частей, с помощью модельных преобразований (обычно композиция переносов, поворотов, масштабирования)

На выходе – модель в единых мировых координатах.

Иерархия преобразований:

Цель – составить «руку робота» с помощью преобразований

Шаг 1: двигаем и поворачиваем блок 1