Математическое описание детерминированных низкочастотных колебаний.

       Здесь широко применяются спектральные и временные методы. При спектральных методах (по Фурье) применяют:

- для периодических сигналов ряд Фурье

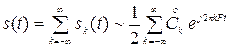
с комплексными амплитудами

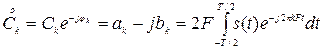
гармоник частоты повторения F=1/T, обладающими свойством ;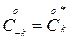

- для непериодических абсолютно интегрируемых сигналов интеграл Фурье

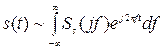
С комплексным спектром (2).

       Часто приходится описывать комплексные сигналы 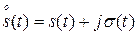, используя интеграл Фурье

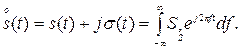
Здесь

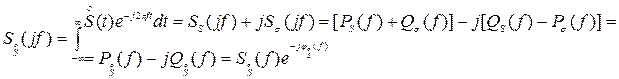
- комплексный спектр комплексного сигнала.

       При спектральных методах описания применяют интеграл Лапласа

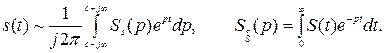
       При временных методах описания применяют интеграл Дюамеля (интеграл свёртки) либо для δ-функции, либо для функции единичного скачка σ₁(t)

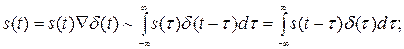
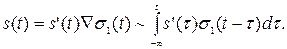
       Распространённым временным методом описания является метод ортогональных разложений

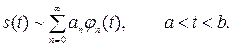
Здесь введены коэффициенты

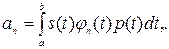
А также ортогональные ортонормированные функции φ₀(t), φ₁(t),…, φ_m(t),…, φ_n(t) с весовой функцией p(t), удовлетворяющие условию ортогональности

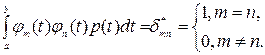
       Среди распространённых ортогональных функций и полиномов (тригонометрические функции, полиномы Лежандра, Лагерра, Эрмита, Чебышева, функции Уолша и др.) особое место занимают функции отсчета

φ_n(t)=sinc(t-n)=sinπ(t-n)/π(t-n),

приводящие к рядам Котельникова во временной области

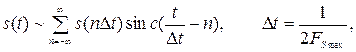
В спектральной области

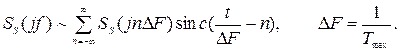
       3.1.3. Математическое описание детерминированных узкополосных колебаний.

Существует несколько способов однозначного определения огибающей и фазы узкополосных квазигармонических колебаний.

1. С помощью двух ортогональных колебаний

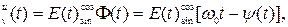       (5)

Приближённо сопряжённых по Гильберту, можно записать огибающую E(t), полную фазу Ф(t) и мгновенную частоту ω_мгн(t) узкополосного колебания в виде

E(t)=[u²(t)+v²(t)]^1/2;

Ф(t)=ω₀t-ψ(t)=arctg[v(t)/u(t)];

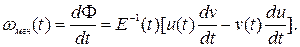
2. С помощью проекций вектора комплексной огибающей

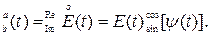
В этом случае

E(t)=[a²(t)+b²(t)]^1/2;

ψ(t)=ω₀t-Ф(t)=arctg[b(t)/a(t)];

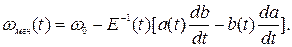
3. С помощью производных узкополосного сигнала

E(t)=[u²(t)+ ω₀^-2 u’²(t)]^1/2;

ψ(t)=ω₀t+arctg[u’(t)/ω₀u(t)];

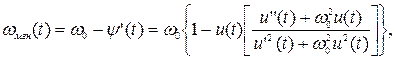
Где      u(t)=u=Ecos(ω₀t-ψ);

       u’(t)=- ω₀Esin(ω₀t-ψ);

       u”(t)=- ω₀² Ecos(ω₀t-ψ).

       При этом соблюдаются важные соотношения

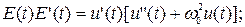
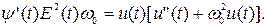
       При описании моделей узкополосных колебаний часто имеют дело с комплексными аналитическими сигналами

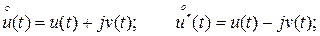 (6)

Так что

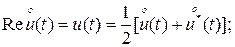(7)

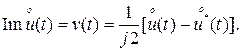
       Иногда требуется определить все компоненты узкополосного сигнала (3) через заданную комплексную огибающую (4):

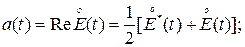
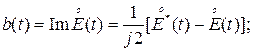 (8)

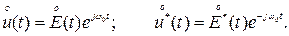
       С помощью формул связи (6)-(8) обычно осуществляют пересчёты комплексных спектров всех компонент узкополосного сигнала (3). Так, основополагающим является соотношение между комплексными спектрами ортогональных сигналов (5), сопряженных по Гильберту:

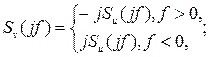
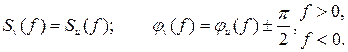
       Весьма удобным методом описания узкополосных сигналов является метод дифференциальных уравнений.

       Математическое описание случайных сигналов и помех осуществляется с помощью обычных методов статистической радиотехники.

3.2. Некоторые алгоритмы цифрового моделирования сигналов ипомех