Алгоритмический метод.

Способ получения последовательностей случайных чисел основан на формировании случайных чисел в ЭВМ с помощью специальных алгоритмов и реализующих их программ. Каждое случайное число вычисляется с помощью соответствующей программы по мере возникновения потребностей при моделировании системы на ЭВМ. Алгоритмический способ получения случайных чисел наиболее рационален на практике при моделировании систем на универсальных ЭВМ.

Рис. 1. Аппаратный способ получения случайных чисел.

При моделировании систем на ЭВМ программная имитация случайных воздействий любой сложности сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию.

Вообще говоря, в качестве базового может быть принят любой удобный в случае моделирования конкретной системы S процесс.

Однако при дискретном моделировании базовым процессом является последовательность чисел {x_i}=x₀, x₁, …, x_N, представляющих собой реализации независимых, равномерно распределенных на интервале (0, 1) случайных величин {ξ_i}=ξ₀, ξ₁,…,ξ_N или – в статистических терминах – повторную выборку из равномерно распределенной на интервале (0, 1) генеральной совокупности значений ξ.

Непрерывная сл.в. x распределена равномерно, если на интервале [a, b) ее плотность постоянна, т.е. имеет вид

Функция распределения F(x) определяется путем интегрирования плотности р(х):

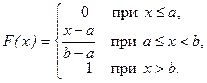
Вид функций р(х) и F(x) показан на рис. 7

1. Математическое ожидание сл.в. x, распределенной по равномерному закону, равно

.                                                        

Действительно,

.

2. Дисперсия равномерного распределения определяется формулой

.                                                    

При моделировании систем на ЭВМ приходится иметь дело со случайными числами интервала (0, 1), когда границы интервала a=0, b=1. Поэтому рассмотрим частный случай равномерного распределения, когда функция плотности и функция распределения соответственно имеют вид

Такое распределение имеет математическое ожидание M[ξ]=1/2 и дисперсию D[ξ]=1/12.

Это распределение требуется получить на ЭВМ. Но получить его цифровой ЭВМ невозможно, так как машина оперирует с n-разрядными числами. Поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0,1) используют последовательность 2ⁿ случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазиравномерным распределением.

4.3. Пример датчика базовой св..

Случайная величина ξ, имеющая квазиравномерное распределение в интервале (0, 1), принимает значения x_i=i/(2ⁿ-1) с вероятностями p_i=1/2ⁿ, .

Математическое ожидание и дисперсия квазиравномерной случайной величины соответственно имеют вид

;

Таким образом, математическое ожидание квазиравномерной случайной величины совпадает с математическим ожиданием равномерной случайной последовательности интервала (0, 1), а дисперсия отличается только множителем (2ⁿ+1)/(2ⁿ-1), который при достаточно больших n близок к 1.

На ЭВМ невозможно получить идеальную последовательность случайных чисел т.к. на ней можно оперировать только с конечным множеством чисел. Кроме того, для получения значений x случайной величины ξ используются формулы (алгоритмы). Поэтому такие последовательности, являющиеся по своей сути детерминированными, называются псевдослучайными.

Прежде чем перейти к описанию конкретных алгоритмов получения на ЭВМ последовательностей псевдослучайных чисел, сформулируем набор требований, которым должен удовлетворять идеальный генератор. Полученные с помощью идеального генератора псевдослучайные последовательности чисел должны: состоять из квазиравномерно распределенных чисел, содержать статистически независимые числа, быть воспроизводимыми, иметь неповторяющиеся числа, получаться с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.

Наибольшее применение в практике моделирования ЭВМ для генерации последовательностей псевдослучайных чисел находят алгоритмы вида 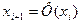(*) представляющие собой рекуррентные соотношения первого порядка, для которых начальное число 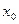и постоянные параметры заданы.

Определим качественно требования к виду функции Ф. Например, легко показать, что функция вида (*), изображенная на рис. 2 (а), не может породить хорошую последовательность псевдослучайных чисел x₁, x₂, … Действительно, если построить точки с координатами (x₁, x₂), (x₃, x₄) по случайным числам, полученным например, из таблицы случайных чисел, то они будут равномерно распределены в единичном квадрате 0≤x_i≤1, 0≤x_i+1≤1. Соответствующие же точки, построенные по числам (x₁, Ф(x₂)), (x₃, Ф(x₄)), …, располагаются в площади, ограниченной кривой .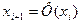

Хорошую последовательность случайных чисел может породить только такая функция 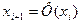, график которой достаточно плотно заполняет единичный квадрат. Примером такой функции может служить  при больших целых положительных А, где Д(u)=u-Ц(u) – дробная часть числа u; Ц(u) – целая часть числа u, т.е. наибольшее целое число не превосходящее u. Пусть для примера А=10, тогда функция 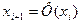 будет иметь вид, показанный на рис. Б. Приведенные условия являются только необходимыми, но не достаточными для того, чтобы соотношение (*) порождало хорошие последовательности псевдослучайных чисел.

Рис 2. Вид функции Ф:

а – неудовлетворяющий; б – удовлетворяющий требованиям генерации.

Рассмотрим некоторые процедуры получения последовательностей псевдослучайных квазиравномерно распределенных чисел, которые нашли применение в практике статистического моделирования систем на ЭВМ.

Одной из исторически первых процедур получения псевдослучайных чисел была процедура, получившая название метода серединных квадратов. Пусть имеется 2n-разрядное число, меньшее 1: x_i=0, a₁, a₂, …, a_2n. Возведем его в квадрат: x₁²=0, b₁, b₂,…,b_4n, а затем отберем средние 2n разрядов x_i+1=0, b_n+1, b_n+2,…,b_3n, которые и будут являться очередным числом псевдослучайной последовательности. Например, если начальное число x₀=0,2152, то (x₀)²=0,04631104, т.е. x₁=0,6311, затем (x₁)²=0,39828721, т.е. x₂=0,8287 и т.д.

Недостаток этого метода – наличие корреляции между числами последовательности, а в ряде случаев случайность вообще может отсутствовать.

     Широкое применение при моделировании систем на ЭВМ получили конгруэнтные процедуры генерации псевдослучайных последовательностей, представляющие собой арифметические операции, в основе которых лежит фундаментальное понятие конгруэнтности.

Два целых числа a и β конгруэнтны (сравнимы) по модулю m, где m-целое число, тогда и только тогда, когда существует такое целое число k, что a-β=km, т.е. разность a-b делится на m и если числа a и b дают одинаковые остатки от деления на абсолютную величину числа m.

Конгруэнтные процедуры являются чисто детерминированными, так как описываются в виде рекуррентного соотношения, когда функция имеет вид (**), где -неотрицательные целые числа.

       Конгруэнтная процедура получения последовательностей псевдослучайных квазиравномерно распределенных чисел может быть реализована мультипликативным либо смешанным методом.

       Мультипликативный метод. Задает последовательность неотрицательных целых чисел {X_i}, не превосходящих М, по формуле

,

Т.е. это частный случай соотношения (**) при .

       В силу детерминированности метода получаются воспроизводимые последовательности. Требуемый объем машинной памяти при этом минимален, а с вычислительной точки зрения необходим последовательный подсчет произведения двух целых чисел, т.е. выполнение операций, которая быстро реализуется современными ЭВМ.

       Смешанный метод. Позволяет вычислить последовательность неотрицательных целых чисел {X_i}, не превосходящих М, по формуле

,

Т.е. в отличие от мультипликативного метода . С вычислительной точки зрения смешанный метод генерации сложнее мультипликативного на одну операцию сложения, но при этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел.

       Качество конкретной версии такого генератора можно оценить только с помощью соответствующего машинного эксперимента.

       В настоящее время почти все библиотеки стандартных программ универсальных ЭВМ для вычисления последовательностей равномерно распределенных случайных чисел основаны на конгруэнтной процедуре.

       Пример датчика базовой СВ: