 |
Главная |
Критические параметры. Форма сопловых и рабочих каналов.
|
из
5.00
|
Отношение давлений  при котором расход достигает наибольшего значения называется критическим. Все параметры (давление - Ркр, скорость - Скр, удельный объем - Vкр, температура - Ткр), соответствующие критическому отношению давлений называются критическими.
при котором расход достигает наибольшего значения называется критическим. Все параметры (давление - Ркр, скорость - Скр, удельный объем - Vкр, температура - Ткр), соответствующие критическому отношению давлений называются критическими.
Для определения критического отношения исследуем функцию 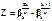 , стоящую в скобках в формуле (2.31), на максимум.
, стоящую в скобках в формуле (2.31), на максимум.
Взяв первую производную и приравняв ее нулю, имеем

откуда критическое отношение давлений
 . (2.32)
. (2.32)
Из выражения (2.32) следует, что критическое отношение давлений зависит только от показателя изознтропии К и для данной рабочей среды есть величина постоянная.
Найдем максимальный расход пара Gtmax и критическую скорость Скр. Для определения максимального расхода подставим в формулу (2.31) вместо β1 критическое отношение давлений. Учитывая выражение (2.32), после преобразований получим
 , (2.33)
, (2.33)
где F1min - площадь минимального сечения сопла (площадь горла). Из формулы (2.33) следует, что при неизменной площади поперечного сечения сопла F1min максимальный расход зависит только от начальных параметров и не зависит от давления за соплом.
Для определения критической скорости подставим критическое отношение давлений в формулу (2.26) и после преобразования получим
 . (2.34)
. (2.34)
Выразим критическую скорость через критические параметры. Из уравнения состояния имеем
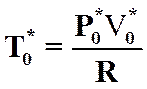 .
.
При изоэнтропийном течении
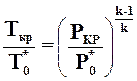
или, учитывая выражение (2.32)
 . (2.35)
. (2.35)
Подставляя в формулу (2.34) значение То*, вычисленное по формуле (2.35), получим
 . (2.36)
. (2.36)
Скорость звука в сплошной среде определяется по выражению
 . (2.37)
. (2.37)
 Из сравнения формул (2.36) и (2.37) следует, что при изоэнтропийном течении критическая скорость равна скорости звука в среде, имеющей температуру, равную критической (Т = Tкр).
Из сравнения формул (2.36) и (2.37) следует, что при изоэнтропийном течении критическая скорость равна скорости звука в среде, имеющей температуру, равную критической (Т = Tкр).
На рис. 2.2 по формулам (2.31) и (2.26) и уравнению изоэнтропы построены кривые, показывающие характер изменения расхода G1t, скорости истечения C1t и удельного объема V1t в выходном сечении сопла в зависимости от отношения давлений β1 при неизменных начальных параметрах рабочего тела.

Рис.2.2 Зависимость расхода через сопло, площади выходного сечения сопла, скорости и удельного объема е выходном сечении от отношения давлений.
Из рисунка видно, что в области дозвукового истечения  при уменьшении β1 (в случае уменьшения давления за соплом) расход возрастает. При критическом течении
при уменьшении β1 (в случае уменьшения давления за соплом) расход возрастает. При критическом течении  расход становится максимальным. В области сверхзвукового истечения
расход становится максимальным. В области сверхзвукового истечения  согласно формуле (2.31) расход должен уменьшаться и при β1 = 0 расход должен быть равен нулю.
согласно формуле (2.31) расход должен уменьшаться и при β1 = 0 расход должен быть равен нулю.
Опыты подтверждают увеличение расхода через сопло при уменьшении β1 в дозвуковой области истечения, но не подтверждают снижение расхода в области сверхзвукового истечения. В действительности, достигнув
|
из
5.00
|
Обсуждение в статье: Критические параметры. Форма сопловых и рабочих каналов. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

