Нахождение кратчайших путей во взвешенных графах между всеми парами вершин.

ВЗВЕШЕННЫЕ ГРАФЫ.  АЛГОРИТМ ФЛОЙДА

План лекции:

1. Определение взвешенных графов, а также взвешенно-направленных графов. Примеры использования различных взвешенных графов и возможный смысл веса ребер.

 

2. Определение графов со взвешенными вершинами. Примеры использования.

 

3. Способы задания взвешенных графов и взвешенно-направленных графов. Графический метод. Матрица смежности, таблица инциденций. Примеры.

 

4. Нахождение кратчайших путей во взвешенных графах между всеми парами вершин. Постановка задачи. Алгоритм Флойда. Описание работы. Примеры.

 

5. Обзор самых распространенных задач и способов их решения: Нахождение каркасных деревьев минимального веса(алгоритмы Краскала и Прима). Нахождение кратчайших путей во взвешенных графах от заданной начальной вершины (алгоритм Дейкстры). Задача коммивояжера.

 

Определение. Граф (орграф) называется взвешенным, если его каждому ребру( дуге) поставлено в соответствие некоторое действительное число .

      Это число называется весом. В качестве весов могут выступать длины дуг, пропускная способность, стоимость эксплуатации, время и т. д.

Замечание: Простой (не взвешенный) граф можно интерпретировать как взвешенный, все рёбра которого имеют одинаковый вес 1.

Определение. Граф (орграф) называется вершинно-взвешенным, если его каждой вершине поставлено в соответствие некоторое действительное число.

Примеры.

Способы задания взвешенных графов и взвешенно-направленных графов:

Графическое изображение.

Матрица смежности.

Для взвешенного графа матрица смежности [A] размера n´n, n=|V| задается следующим образом:

 

где w(v_i,v_j) R – вес («стоимость») ребра (дуги).

Для ненаправленных графов матрица смежности симметрична относительно главной диагонали.

Замечание. Иногда вместо 0 в случае отсутствие ребер ставят знак бесконечности или прочерк. Но на главной диагонали элементы остаются равными нулю.

3. Таблица инциденций. Строка таблицы инциденций содержит вершину Vi с перечислением всех смежных ей вершин и указанием веса ведущего к ним ребра.

Примеры.

Нахождение кратчайших путей во взвешенных графах между всеми парами вершин.

Определение. Путь во взвешенном графе из вершины v_i в v_j называется минимальным, если он имеет минимальную длину(сумму весов ребер) среди всех путей из вершины v_i   в v_j.

Алгоритм Флойда–Уоршелла является точным алгоритмом Разработан в 1962 году американскими учеными Робертом Флойдом и Стивеном Уоршеллом, хотя в 1959 г. Бернард Рой опубликовал практически такой же алгоритм, но это осталось незамеченным.

Алгоритм изначально оперирует с матрицей весов[W(i,j)], которая является разновидностью взвешенной матрицы смежности:

[W(i,j)]=

 

где w(v_i,v_j) – вес ребра (дуги) { v_i,v_j };

Алгоритм выполняет n (k меняется от 1 до n) проходов, в течении которых  элементы матрицы вычисляются по формуле:

W(i,j)=min {W(i,j),W(i,k)+W(k,j)},

которая означает, что если путь через вершину V(k) является короче найденного ранее, то он и выбирается.

Т.е. на каждом шаге алгоритм генерирует двумерную матрицу W.

Псевдокод

for k = 1 to n

for i = 1 to n

for j = 1 to n

W[i][j] = min(W[i][j], W[i][k] + W[k][j])

Результатом выполнения алгоритма Флойда является матрица достижимости, элементы которой равны найденному кратчайшему пути между соответствующими каждому элементу вершинами.

Сложность алгоритма Флойда: Три вложенных цикла содержат операцию, исполняемую за линейно зависимое от n время, поэтому алгоритм имеет кубическую сложность – О(n³), n=|V|.

Пример. С помощью алгоритма Флойда найти кратчайшие пути между всеми парами вершин графа.

Решение.

Для выполнения алгоритма Флойда построим матрицу весов, которая является разновидностью матрицы смежности:

.

Выполним проход матрицы для каждой из вершин графа. Если путь через вершину прохода короче, то он и выбирается. Столбец, соответствующий вершине E не изменится, так как в вершину E не входит ни одна дуга.

 

1) Проход через вершину А. С помощью построенной матрицы (а не по графу) сравниваем пути. Например, между вершинами C и B «расстояние» , а путь C – А – B равен 8, поэтому меняем соответствующий элемент в матрице на меньший. Получаем следующую матрицу:

.

 

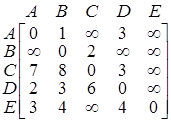2) Проход через вершину B. Выполняется аналогично, но основой для его выполнения служит матрица, полученная в результате прохода через матрицу А.

.

 

3) Проход через вершину С.

.

4) Проход через вершину D.

.

 

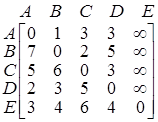5) Проход через вершину E.

.

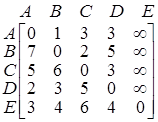В результате этого прохода матрица не изменилась, так как в вершину Е не входит ни одна дуга, а следовательно путь из одной вершины в другую через Е невозможен.

 

Ответ: матрица расстояний между вершинами графа имеет вид:

.

 

Обзор самых распространенных задач и способов их решения: Нахождение каркасных деревьев минимального веса(алгоритмы Краскала и Прима). Нахождение кратчайших путей во взвешенных графах от заданной начальной вершины (алгоритм Дейкстры). Задача коммивояжера.