 |
Главная |
Прямые методы решения СЛАУ. Метод Гаусса и его модификации с выбором главного элемента
|
из
5.00
|
Метод бисекции.
Постановка задачи: Отыскание корней нелинейного уравнения с одним неизвестным вида: f(x)=0

Скорость сходимости:
Сходится со скоростью геометрической прогрессии, знаменатель которой равен q=1/2
Оценка погрешности:

Видно, что метод сходится со скоростью геометрической прогрессии. В сравнении с другими методами сходится довольно медленно.
Критерий окончания:

4.Метод простой итерации
Постановка задачи: Отыскание корней нелинейного уравнения с одним неизвестным вида: f(x)=0
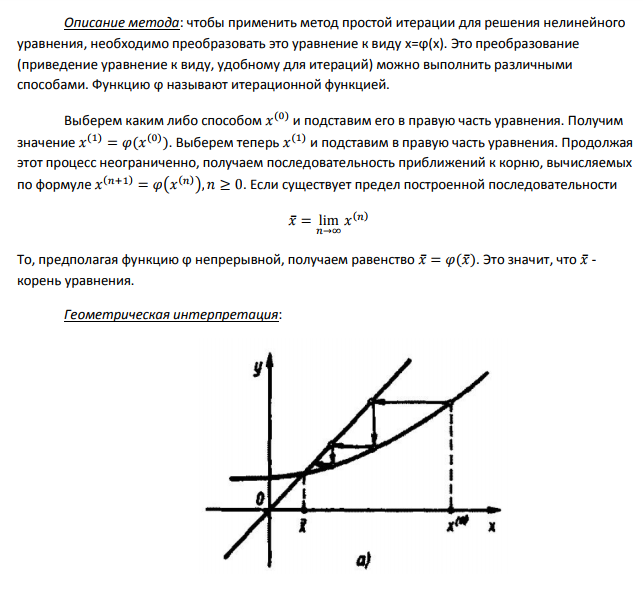
Скорость сходимости:
Сходится со скоростью геометрической прогрессии.
Пусть в (дельта) окрестности корня х функция дифференцируема и удовлетворяет неравенствам
|ϕ ‘(x)|<=q
0<=q<=1, справедлива априорная оценка погрешности:

Апостериорная оценка погрешности:

Критерий окончания:
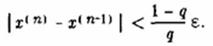
5.Метод Ньютона(метод касательных)
Постановка задачи: Отыскание корней нелинейного уравнения с одним неизвестным вида: f(x)=0
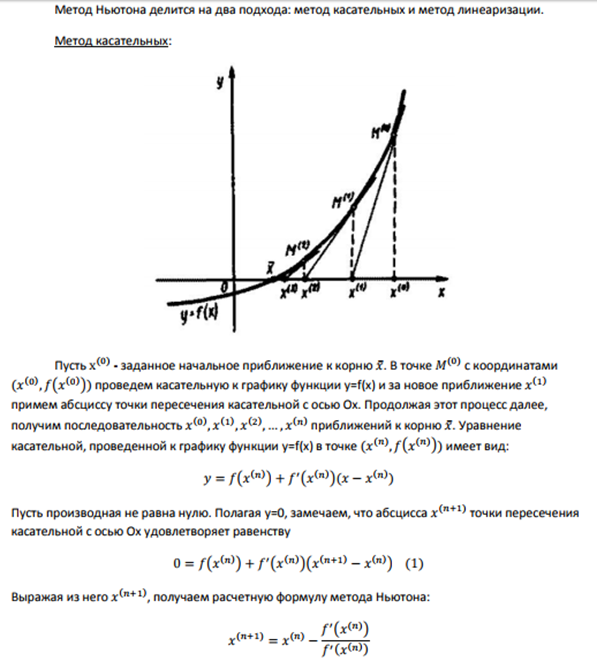

Скорость сходимости:
Пусть х простой корень уравнения в окрестности которого функция дважды дифференцируема. Тогда существует такая Ϭ окрестность корня х, что для любого начального приближения х(0) итерационная последовательность метода Ньютона сходится с квадратичной зависимостью.
 С= Ϭ -1
С= Ϭ -1
Следствием является априорная оценка

в которой

Критерий окончания :

Недостатки метода:
-необходимость вычисления производной
-метод обладает только начальной сходимостью
6. Постановка задачи поиска корня нелинейного уравнения. Модификации метода Ньютона (у прощенный метод Ньютона, метод ложного положения, метод секущих их др.).
Постановка задачи: Отыскание корней нелинейного уравнения с одним неизвестным вида: f(x)=0



7.Обусловленность задачи вычисления корня нелинейного уравнения.
Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым погрешностям входных данных.
Пусть установлено неравенство  , где
, где  - относительная погрешность входных данных, а
- относительная погрешность входных данных, а  - относительная погрешность решения. Тогда
- относительная погрешность решения. Тогда  - называется абсолютным числом обусловленности задачи. Если же установлено неравенство
- называется абсолютным числом обусловленности задачи. Если же установлено неравенство  между относительными погрешностями данных и решения, то
между относительными погрешностями данных и решения, то  называют относительным числом обусловленности задачи.
называют относительным числом обусловленности задачи.
Обычно под числом обусловленности  понимают относительное число обусловленности. Если
понимают относительное число обусловленности. Если  , то задачу называют плохо обусловленной.
, то задачу называют плохо обусловленной.
Обусловленность задачи нахождения корня. Пусть  v корень, подлежащий определению. Будем считать, что входными данными для задачи вычисления корня являются значения функции
v корень, подлежащий определению. Будем считать, что входными данными для задачи вычисления корня являются значения функции  . Так как
. Так как  вычисляется приближенно, то обозначим функцию, полученную в действительности через
вычисляется приближенно, то обозначим функцию, полученную в действительности через  . Предположим, что в малой окрестности корня выполняется неравенство:
. Предположим, что в малой окрестности корня выполняется неравенство:  .
.
Для близких к  значений
значений  справедливо равенство
справедливо равенство  , следовательно,
, следовательно,  . Это означает, что число обусловленности задачи нахождения корня равно
. Это означает, что число обусловленности задачи нахождения корня равно  . Из последней формулы следует, что чем меньше значение производной функции в точке корня, тем задача хуже обусловлена. В частности, задача нахождения кратного корня имеет число обусловленности - бесконечность.
. Из последней формулы следует, что чем меньше значение производной функции в точке корня, тем задача хуже обусловлена. В частности, задача нахождения кратного корня имеет число обусловленности - бесконечность.
8.Постановка задачи решения системы линейных алгебраических уравнений (СЛАУ).
Норма вектора, норма матрицы. Обусловленность задачи решения СЛАУ.
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
 ,
,
Эту систему уравнений можно записать также в матричном виде:
 ,
,
где  ,
, 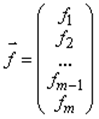 ,
,  .
.
A–матрица системы,  – вектор правых частей,
– вектор правых частей, 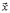 – вектор неизвестных.
– вектор неизвестных.
При известных A и  требуется найти такие
требуется найти такие  , при подстановке которых в систему уравнений она превращается в тождество.
, при подстановке которых в систему уравнений она превращается в тождество.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
Нормы векторов и матриц. Обозначим через  - точное решение системы, а через
- точное решение системы, а через  - приближенное решение системы. Для количественной характеристики вектора погрешности
- приближенное решение системы. Для количественной характеристики вектора погрешности 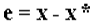 введем понятие нормы.
введем понятие нормы.
Нормой вектора  называется число
называется число  , удовлетворяющее трем аксиомам:
, удовлетворяющее трем аксиомам:
1) 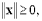 причем
причем  = 0 тогда и только тогда, когда
= 0 тогда и только тогда, когда  = 0;
= 0;
2)  для любого вектора
для любого вектора  и любого числа
и любого числа  ;
;
3)  для любых векторов
для любых векторов  и
и  .
.
Наиболее употребительными являются следующие три нормы:
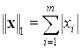 ,
,  ,
,  .
.
Абсолютная и относительная погрешности вектора вводятся с помощью формул:
 и
и 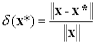 .
.
Нормой матрицы  называется величина
называется величина  .
.
Введенная норма обладает свойствами, аналогичными свойствам нормы вектора:
1)  причем
причем  = 0 тогда и только тогда, когда A = 0;
= 0 тогда и только тогда, когда A = 0;
2) 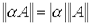 для любой матрицы A и любого числа
для любой матрицы A и любого числа  ;
;
3)  для любых матриц A и B;
для любых матриц A и B;
4)  .
.
Каждой из векторных норм соответствует своя подчиненная норма матрицы:
 ,
,  ,
,  .
.
В оценках вместо нормы  используется евклидова норма матрицы
используется евклидова норма матрицы
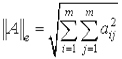 , так как
, так как  .
.
Абсолютная и относительная погрешности матрицы вводятся аналогично погрешностям вектора с помощью формул:
 ,
,  .
.
Обусловленность задачи решения СЛАУ. С задачей решения системы линейных уравнений  (А-элементы матрицы заданы точно, b – вектор-столбец задан приближенно) связаны задачи решения соответствующих возмущённых систем
(А-элементы матрицы заданы точно, b – вектор-столбец задан приближенно) связаны задачи решения соответствующих возмущённых систем  ,
,  или
или  . Для возмущённых систем первого и второго вида относительная погрешность решения
. Для возмущённых систем первого и второго вида относительная погрешность решения  связана с относительными погрешностями исходных данных
связана с относительными погрешностями исходных данных  и
и  соответственно следующими неравенствами:
соответственно следующими неравенствами:
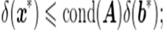
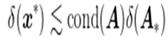
а для возмущённых систем третьего типа, при  , неравенством
, неравенством
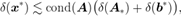 где
где  — стандартное число обусловленности, или просто число обусловленности. Оно имеет следующий простой смысл: его порядок приблизительно показывает максимально возможную потерю верных цифр при решении возмущённой системы линейных алгебраических уравнений. Системы с большим числом обусловленности матрицы, для которых
— стандартное число обусловленности, или просто число обусловленности. Оно имеет следующий простой смысл: его порядок приблизительно показывает максимально возможную потерю верных цифр при решении возмущённой системы линейных алгебраических уравнений. Системы с большим числом обусловленности матрицы, для которых 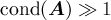 , обычно считают плохо обусловленными, хотя нередко реальная погрешность решения оказывается существенно меньше погрешности, вычисляемой в соответствии с правыми частями приведённых неравенств.
, обычно считают плохо обусловленными, хотя нередко реальная погрешность решения оказывается существенно меньше погрешности, вычисляемой в соответствии с правыми частями приведённых неравенств.
Число обусловленности обладает следующими тремя основными свойствами:
1)  ;
;
2)  ;
;
3) для любого числа  справедливо равенство
справедливо равенство 
Прямые методы решения СЛАУ. Метод Гаусса и его модификации с выбором главного элемента
Прямыми методами называются методы, позволяющие получить решение системы  за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
Метод Гаусса
Постановка задачи: Найти решение системы m линейных уравнений.
Запишем систему Ax=f, в развернутом виде

Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что 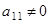 . Последовательно умножая первое уравнение на
. Последовательно умножая первое уравнение на 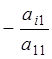 и складывая с i-м уравнение, исключим
и складывая с i-м уравнение, исключим 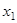 из всех уравнений кроме первого. Получим систему
из всех уравнений кроме первого. Получим систему


Аналогичным образом из полученной системы исключим  .
.
Последовательно, исключая все неизвестные, получим систему треугольного вида

Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все  ,
,  не равны нулю.
не равны нулю.
Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.

 .
.
Эта процедура получила название обратный ход метода Гаусса..
Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). На k-ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент аik,k при неизвестной  в уравнениях с номерами i = k+1.. m. Затем уравнение, соответствующее выбранному коэффициенту с номером
в уравнениях с номерами i = k+1.. m. Затем уравнение, соответствующее выбранному коэффициенту с номером  , меняю местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента
, меняю местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента  . После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.
. После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.
10.Прямые методы решения СЛАУ. LU - разложение матрицы и его использование.
Прямыми методами называются методы, позволяющие получить решение системы 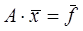 за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
LU –метод
LU-метод основан на том, что если главные миноры матрицы А отличны от нуля, тогда матрицу А можно представить, причем единственным образом, в виде произведения
А=LU,
где L–нижняя треугольная матрица с ненулевыми диагональными элементами и U–верхняя треугольная матрица с единичной диагональю.
Рассмотрим СЛАУ Ax=f.


A=LU
где


или
 ,
,


Окончательно запишем


Полагая  получим следующие рекуррентные формулы для вычисления элементов матрицы L и U
получим следующие рекуррентные формулы для вычисления элементов матрицы L и U

Если найдены матрицы L и U, то решение исходной системы сводится к последовательному решению двух систем уравнений с треугольными матрицами
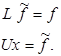
LU – метод позволяет вычислить определитель матрицы А
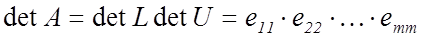
|
из
5.00
|
Обсуждение в статье: Прямые методы решения СЛАУ. Метод Гаусса и его модификации с выбором главного элемента |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

