Значимости по новым данным

 

	Y	X1	X2	X3	X4	X5
Y	1,0000	,2211	,1599	,5640	,7294	-,1510
	p= ---	p=,513	p=,620	p=,071	p=,011	p=,658
X1	,2211	1,0000	-,2864	-,1358	-,0557	,4157
	p=,513	p= ---	p=,393	p=,691	p=,871	p=,204
X2	,1599	-,2864	1,0000	,1763	,2854	-,4720
	p=,620	p=,393	p= ---	p=,604	p=,395	p=,056
X3	,5640	-,1358	,1763	1,0000	,1244	-,4779
	p=,071	p=,691	p=,604	p= ---	p=,634	p=,052
X4	,7294	-,0557	,2854	,1244	1,0000	-,4435
	p=,011	p=,871	p=,395	p=,634	p= ---	p=,172
X5	-,1510	,4157	-,4720	-,4779	-,4435	1,0000
	p=,658	p=,204	p=,056	p=,052	p=,172	p= ---

 

 

2.4. Построение регрессионной модели.

 

На предыдущем этапе была исследована взаимосвязь результирующего признака Y с каждым из признаков факторного набора. В результате была обнаружена статистически значимая на уровне 5% прямая умеренная связь Ус фактором х4, причем влияние фактора х4 на  результирующий признак происходит с временным лагом τ=4, и была обнаружена статистически значимая на уровне 10% прямая сильная связь между х3 и у, влияние фактора х3 на результирующий признак происходит с временным лагом τ=0 . Построим множественную  регрессионную модель, отражающую зависимость количества людей, у которых наследственная предрасположенность к сахарному диабету(х4) болезнь эндокринной системы(х3) на  количество людей с сахарным диабетом(Y). Для построения модели ряд х4 предварительно сдвигаются относительно ряда Y на 4 периода, а х3 остается на месте.

 

	Y_1 D(-1)	X1_1 D(-1); D(-1)	X2_1 D(-1)	X3_1 D(-1)	X4_1 D(-1); D(-1)
1	0,077		0,012	0,027		-0,034
2	0,023	-0,003	0,049	0,019		-0,070
3	0,360	-0,004	0,023	0,031		-0,038
4	0,110	0,007	-0,010	0,003		-0,054
5	0,174	0,051	0,040	0,020	-0,002	0,035
6	0,026	-0,034	0,060	0,030	-0,002	0,021
7	0,080	-0,004	0,016	0,050	0,002	0,059
8	0,250	0,084	0,031	0,048	-0,028	0,044
9	-0,400	0,002	0,002	0,002	0,005	0,029
10	0,176	-0,052	0,025	0,076	-0,001	-0,021
11	-0,076	0,003	0,062	0,042	0,013	-0,017
12	0,190	0,018	0,047	0,131	0,002	-0,033
13	0,010	-0,029	0,034	0,053	-0,006	-0,026
14	0,350	0,016	0,081	0,089	0,006	-0,013
15	0,090	-0,034	0,318	0,159	0,002	-0,115
16	0,030	0,029	0,023	0,060	0,007	-0,009

 

Построение множественной регрессионной модели:

 

Таблица1. Результаты регрессионного анализа

R= ,68548172 R?= ,46988518 Adjusted R?= ,41098354
F(1,9)=7,9775>Fтабл=4,6 p<,01990 Std.Error of estimate: ,15081
	Beta	Std.Err. of Beta	B	Std.Err. of B	t(9)	p-level
Intercept			0,07683	0,045634	1,683522	0,000001
X4	0,685482	0,242697	13,13043	4,648864	2,824439	0,000027
Х3	0,601229	0,224326	0,100278	0,037415	2,68016	0,000234

 

Y=0,07683+0,100278х3+13,13043x4- полученное уравнение.

Исследуем на адекватность построенное линейное уравнение регрессии:

Для исследования полученной модели на адекватность воспользуемся:

1.Коэффициентом детерминации;

2.критерием Фишера;

3.критерием Стьюдента;

4.проведем анализ остатков.

Общий и скорректированный коэффициент детерминации

 

R= ,68548172 R?= ,46988518 Adjusted R?= ,41098354

Оба этих коэффициента не сильно близки к 1. Следовательно, можно сделать вывод об умеренном влиянии факторных признаков на результирующий показатель.

 

Критерий Фишера

Проверим на значимость генеральное уравнение линейной регрессии Y=b₀+b₁Т

Построим гипотезы:

Но : уравнение не значимо (b₀=b₁=0);

Н1 : уравнение значимо. (b_j¹0).

1.Если F_расч >F_табл, то с вероятностью не менее 95% можно утверждать, что принимается гипотеза Н1.

2.Если модуль F_расч <F_табл, то с вероятностью 95% нельзя утверждать, что принимается гипотеза Н1.[10]

a =0.05; n₁ =1; n₂=14;

F_0,05;1;92 =4,6

F_{расчет.} =7,9775

Это означает, что с вероятностью не менее 95% можно утверждать, что уравнение значимо.

 

Критерий Стьюдента

На основе данных последней таблицы можно говорить о значимости коэффициентов регрессии βj :

t0= 1,683522 βo значим на уровне 0,000001

t1=2,824439 β1 значим на уровне 0,000027

t2=2,68016 β2 значим на уровне 0,000234

Анализ остатков

Для полученной модели проведем проверку условий Гаусса-Маркова.

Построим график распределения остатков на нормальной вероятностной бумаге и гистограмму остатков.

Рис. 4.1. График распределения остатков на нормальной вероятностной бумаге.

 

 

Рис. 4.2. Гистограмма остатков

С помощью гистограммы и графика на нормальной вероятностной бумаге делаем вывод о том, что распределения остатков близко к нормальному закону распределения. Следовательно, можно проанализировать выполнение условий Гаусса-Маркова.

Проверка условий Гаусса-Маркова:

Ое и 4-ое условия

Рис7. Математическое ожидание остатков

 

Из данного графика можно сделать вывод о том, что математическое ожидание остаточной компоненты равно нулю, т.к. линия математического ожидания находится на нулевом уровне, и остатки независимы с объясняющей переменной, т.к. коэф.корреляции=0. Следовательно, 1 и 4 условия Гаусса-Маркова выполняются.

 

2-ое условие:

.

 

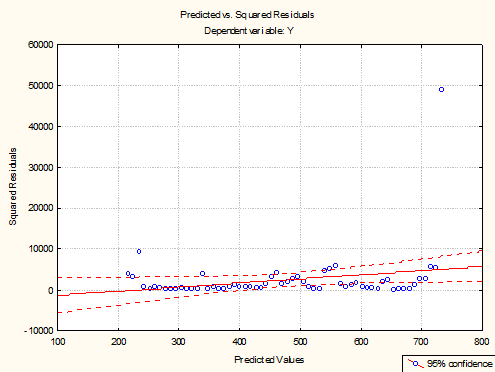
Рис8. Дисперсия остатков

 

Из графика видно, что линия дисперсий остатков не параллельна оси Х, наклон идет вверх, дисперсия случайного возмущения увеличивается.

Следовательно, 2-ое условие Гаусса-Маркова не выполняются

 

3-е условие (проверка автокорреляции остатков):

 

Критерий Дарбина-Уотсона:

	Durbin- Watson d	Serial Corr.
Estimate	2,558753	-0,302355

 

Табличное значение коэффициента d при N = 14, m = 1 составляет d^н =1,045 и d^в= 1,330; 4-d^в=2,670

Т. к. расчетное значение d=2,558753, то принадлежит промежутку (d^в;4-d^в), автокорреляция отсутствует. Условие выполняется.

Таким образом, можно сделать вывод, что модель адекватна, хотя выполняются не все условия Гаусса – Маркова (не выполняется 2 условие), но уравнение значимо по критерию Фишера и Стьюдента.

Заключение

 

В результате исследования было выявлено, что основными причинами болезни сахарного диабета в городе Красноярске с 1991 года по 2007 год являются наследственная предрасположенность и больные эндокринной системы, как и предполагалось в первой главе курсовой. Это означает, что вероятнее всего заболеть тем людям, у которых родственники болеют сахарным диабетом и тем, у кого имеется болезнь эндокринной системы.

Исследуя эту тему, я глубоко изучила сахарный диабет, это очень страшная болезнь, которая влияет на весь человеческий организм.

И чтобы хоть немного уменьшить вред от диабета нужно самое главное - регулярно посещать врача и выполнять его рекомендации по поводу диабета:

1.Соблюдать диету!

2.Витамины. Увы, но большая часть людей, включая больных диабетом, страдает заболеваниями желудка и кишечника, поэтому даже если они регулярно едят фрукты и овощи или принимают витаминные драже, они все же страдают от дефицита витаминов. Диабетикам рекомендуется два раза в год делать курсы внутримышечных инъекций витаминов. После таких курсов часто улучшается общее самочувствие, уменьшаются боли в ногах, общее течение диабета улучшается.

3.Сосудистые лекарства, средства, защищающие почки, лекарства от повышенного давления. Давление у диабетика должно быть нормальным (не выше 140/90)! От этого напрямую зависит продолжительность жизни. 4.Физиотерапия.

5.Массаж. Ежедневный массаж стоп поможет избежать осложнений диабета.

6.Физкультура.