 |
Главная |
Функционалы метода наименьших квадратов
|
из
5.00
|
Идентификация параметров осциллирующих процессов в живой природе, моделируемых дифференциальными уравнениями
Выполнила студентка 312гр.
Варламова А.А.
Проверил Токин И.Б
Санкт-Петербург
2007
Оглавление
1. Идентификация параметров в системах описываемых ОДУ
1.1 Градиентные уравнения
1.2 Уравнения в вариациях
1.3 Функционалы метода наименьших квадратов
1.4 Численное решение градиентных уравнений
1.4.1 Полиномиальные системы
1.4.2 Метод рядов Тейлора
1.4.3 Метод Рунге-Кутта
2. Модели осциллирующих процессов в живой природе
2.1 Модель Лотки
2.1.1 Осциллирующие химические реакции
2.1.2 Осцилляция популяций в системе “хищник-жертва”
2.2 Другие модели
3. Идентификация параметров модели Лотки
3.1 Дифференциальные уравнения
3.2 Постановки задачи идентификации и функционалы МНК
3.3 Как ускорить вычисления
3.4 Численный эксперимент
4. О других методах идентификации
Литература
Идентификация параметров в системах, описываемых ОДУ
Градиентные уравнения
Градиентные уравнения возникают в связи с задачей нахождения экстремумов функций многих аргументов. Важно, что эти аргументы сами могут зависеть от решений каких-то уравнений - численных, дифференциальных и иных. Мы будем использовать их для минимизации функций аргументов, за-висящих от решений обыкновенных дифференциальных уравнений.
Рассмотрим вещественнозначную функцию 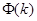 аргумента
аргумента 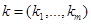 ,
, 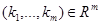 и пусть
и пусть 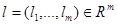 и
и 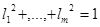 . Тогда величина
. Тогда величина
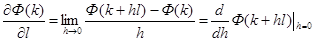 (1)
(1)
то есть производная функции 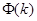 по направлению
по направлению 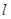 характеризует скорость изменения
характеризует скорость изменения 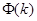 при изменении
при изменении 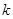 в направлении вектора
в направлении вектора 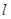 .
.
Из формулы (1) получаем:
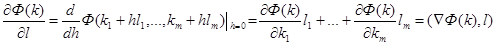 (2)
(2)
где 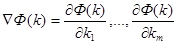 - градиент функции
- градиент функции 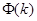 , а это дает:
, а это дает:
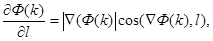 (3)
(3)
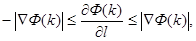 (4)
(4)
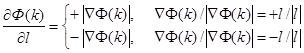 (5)
(5)
Таким образом, вектор 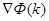 является направлением наискорейшего рос-та функции
является направлением наискорейшего рос-та функции 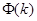 в точке
в точке 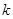 , а вектор
, а вектор 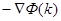 - это направление наискорейшего ее убывания в этой точке.
- это направление наискорейшего ее убывания в этой точке.
Градиентной кривой функции 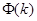 называют кривую
называют кривую 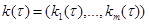 ,
, 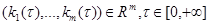 , касательное направление к которой в каждой точке
, касательное направление к которой в каждой точке 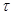 противоположно направлению вектора градиента
противоположно направлению вектора градиента 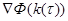 , то есть сов-падает с направлением наискорейшего убывания
, то есть сов-падает с направлением наискорейшего убывания 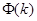 .
.
Это означает, что 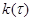 удовлетворяет дифференциальному уравнению:
удовлетворяет дифференциальному уравнению:
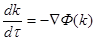 (6)
(6)
или в координатной форме:
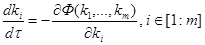 (7)
(7)
К уравнениям (6) или (7) добавляем начальные условия:
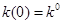 (8)
(8)
или в координатной форме:
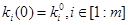 (9)
(9)
Решение задачи Коши (6),(8) (или (7),(9)) определяет градиентную кривую проходящую через точку 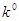 . Будем рассматривать это решение как век-тор-функцию
. Будем рассматривать это решение как век-тор-функцию 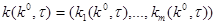 аргументов
аргументов 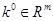 и
и 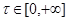 .
.
Зададимся теперь целью найти точку 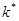 локального минимума неотрицательной функции
локального минимума неотрицательной функции 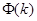 , если она существует и достаточно близка к
, если она существует и достаточно близка к 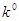 . Если за начальное приближение для
. Если за начальное приближение для 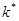 взять
взять 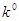 , то движение вдоль градиентной кривой, проходящей через
, то движение вдоль градиентной кривой, проходящей через 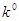 (то есть движение вдоль траектории решения
(то есть движение вдоль траектории решения 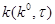 ) можно считать идеальным путем к точке
) можно считать идеальным путем к точке 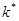 .
.
Если решение задачи (6),(8) существует при 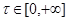 , то при любом та-ком
, то при любом та-ком 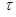 получаем, что:
получаем, что:
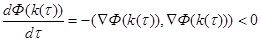 при
при 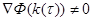 (11)
(11)
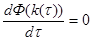 при
при 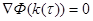 (12)
(12)
и мы вправе ожидать, что
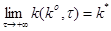 (13)
(13)
Метод градиентных уравнений нахождения локального минимума функции 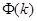 заключается в численном интегрировании задачи Коши (6),(8) вдоль оси
заключается в численном интегрировании задачи Коши (6),(8) вдоль оси 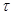 до достижения точки
до достижения точки 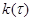 , достаточно близкой к
, достаточно близкой к 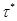 .
.
Уравнения в вариациях
Рассмотрим задачу Коши:
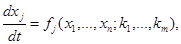 (14)
(14)
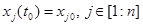 (15)
(15)
где 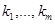 - параметры. В дальнейшем мы рассмотрим функционалы, зависящие от параметров
- параметры. В дальнейшем мы рассмотрим функционалы, зависящие от параметров 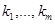 через решение задачи Коши (14),(15). Тогда градиентные уравнения будут зависеть от производных по
через решение задачи Коши (14),(15). Тогда градиентные уравнения будут зависеть от производных по 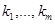 решения задачи (14),(15), и мы должны уметь их вычислять. Дифференцируя уравнения (14), (15) по
решения задачи (14),(15), и мы должны уметь их вычислять. Дифференцируя уравнения (14), (15) по 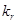 получаем, что функции
получаем, что функции
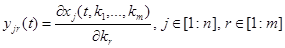 (16)
(16)
удовлетворяют следующей задаче Коши:
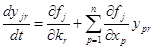 (17)
(17)
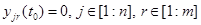 (18)
(18)
Уравнения (17) относительно производных (16) называют уравнениями в вариациях для уравнений (14).
Функционалы метода наименьших квадратов
Мы не можем рассмотреть здесь все многообразие функционалов метода наименьших квадратов и ограничимся одним достаточно общим функционалом. Он соответствует следующей задаче: модель некоторого процесса описывается задачей Коши (14),(15) (такие модели, в частности, достаточно распространены в биологической кинетике), даны измерения
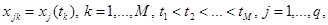 , (19)
, (19)
то есть даны 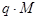 приближений для значений величин
приближений для значений величин 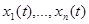 в моменты времени
в моменты времени 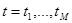 , и требуется найти параметры
, и требуется найти параметры 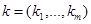 на основе заданного начального приближения
на основе заданного начального приближения 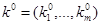 .
.
В методе наименьших квадратов нахождения (идентификации) параметров 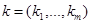 рассматривают функционал
рассматривают функционал
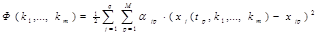 (20)
(20)
где 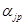 - фиксированные весовые коэффициенты, а
- фиксированные весовые коэффициенты, а 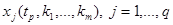 - значения первых
- значения первых 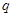 компонент решения задачи (14),(15) в точке
компонент решения задачи (14),(15) в точке 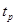 при заданных
при заданных 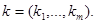
В методе наименьших квадратов полагают, что значение 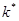 , доставляющее минимум этой функции
, доставляющее минимум этой функции 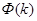 , является адекватным приближением к реальному значению параметра
, является адекватным приближением к реальному значению параметра 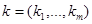 для принятой модели процесса.
для принятой модели процесса.
Для того, чтобы воспользоваться методом градиентных уравнений, необходимо выписать уравнения (7) для функционала (20):
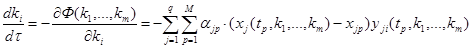 (21)
(21)
Эти градиентные уравнения надо дополнить начальными условиями:
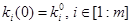 (22)
(22)
|
из
5.00
|
Обсуждение в статье: Функционалы метода наименьших квадратов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

