Основные математические аспекты теории игр

Глава 14. Методы и модели теории игр

Теория игр — это раздел  исследования операций,  изучающий процесс, в котором участвуют две и более сторон, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков, которые могут быть нейтральными (статистические игры) или действовать логично  с целью получения максимума выгоды (стратегические игры). Теория игр помогает выбрать лучшие стратегии с учётом представлений о других участниках, их  ресурсах и их возможных поступках.

Впервые математические аспекты и приложения теории игр были изложены в 1950-х г. в трудах венгерского математика Джона фон Неймана.  Первые концепции теории игр анализировали антагонистические игры, когда есть проигравшие и выигравшие за их счет игроки. Развитие теория стратегических игр получила в трудах американского математика, лауреата Нобелевской премии 1994г. Дж. Нэша, где разрабатываются  принципы «управленческой динамики» и соответствующие им методы анализа, в которых все участники или выигрывают, или терпят поражение. Эти ситуации получили названия «равновесие по Нэшу», или «некооперативное равновесие». Современная концепция статистического решения выдвинута А.Вальдом.  В настоящее время получили развитие динамические игры.

В данном разделе изложены базовые модели теории игр для двух игроков.

Более подробную информацию можно найти в учебной литературе [1-10]. 

Основные математические аспекты теории игр

Теория игр изучает и рассматривает методы определения оптимального поведения при управлении системами, в которых характерно наличие конфликтной ситуации (столкновение интересов).

Основные определения. Под конфликтом понимается всякое явление, применительно к которому можно говорить, кто и как в этом явлении участвует, каковы могут быть у этого явления исходы, кто в этих исходах заинтересован и в чем эта заинтересованность состоит.

Для конфликтов характерно то, что ни один из его участников заранее не знает решений, принимаемых остальными участниками. Другими словами, участники конфликтов вынуждены действовать в условиях риска и неопределенности. Неопределенность исходов может проявляться не только в результате сознательных действий других участников, но и как результат действия тех или иных стихийных сил.

Математическую модель конфликтной ситуации называют игрой. Как и всякая математическая модель, игра является упрощением реального конфликта, отражает только основные первостепенные факторы.

 Стороны, участвующие в такой ситуации называют игроками. Возможные действия игроков, определенные правилами игры, называют стратегиями.

Правилами игры предусматриваются определенные выигрыши для игроков в зависимости от применяемых ими стратегий и исходов игры. Выигрыш – это мера эффекта для игрока. В теории игр он измеряется количественно.

Стратегия игрока называется оптимальной, если она обеспечивает данному игроку при многократном повторении игры максимально -возможный средний выигрыш или минимально возможный средний проигрыш [5].

Игры можно классифицировать по различным критериям.

· По количеству игроков различают игры  двух и n -игроков.

· По количеству стратегий игры делятся конечные и бесконечные. В свою очередь,  если число стратегий можно перенумеровать, то игра с бесконечным числом стратегий называется сепарабельной, если нельзя – непрерывной

· По количеству ходов выделяют одношаговые  игры, в которых каждый игрок делает ход и после этого делятся выигрыши, и многошаговые. В свою очередь многошаговые игры можно поделить на позиционные, в которых участвуют несколько игроков и каждый может делать последовательно несколько ходов, стохастические, когда известны вероятности достижения каждой позиции, и дифференциальные, когда ходы делаются непрерывно и поведение игроков описывается дифференциальным уравнением.

· По характеру взаимоотношений: бескоалиционные (игроки не имеют права вступать в соглашения), коалиционные (игроки могут вступать в соглашения, создавать коалиции), кооперативные (коалиции определены заранее).

· Характер выигрышей: игры с нулевой суммой (сумма выигрышей всех игроков равна нулю), игры с ненулевой суммой (пример – торговые отношения между странами)

· Характер неопределенности игровой ситуации: комбинаторные (число исходов, стратегий, факторов конечно и не очень большое), случайные (количество исходов не зависит от поведения игрока), стратегические (один из участников находится в состоянии неопределенности относительно поведения других участников игры)- в теории принятия решений статистические игры являются основным подходом, если решение принимается в условиях частичной неопределенности. Статистические модели представляют собой игру двух лиц (человека и природы) с использованием человеком дополнительной статистической информации о состояниях природы.

· Вид функции выигрыша: матричные (конечная игра двух лиц с нулевой суммой, функция выигрыша задана в виде матрицы), биматричные (для каждого из участников заданы свои матрицы выигрышей, игра с ненулевой суммой), непрерывные (функция выигрыша является непрерывной).

Поскольку математический аппарат стратегических игр является более широким и охватывает статистические игры, остановимся на первом более подробно.

Стратегические игры. Решение матричной игры в чистых стратегиях. Пусть в игре заняты два игрока А и В, каждый из которых имеет конечное число стратегий: игрок А располагает стратегиями  А₁, А₂, …А_n ; у игрока В имеются стратегии В₁,В₂,…В_m.

Предполагается, для каждой комбинации стратегий (А_i,B_j) известна величина выигрыша a_ij игрока А, причем выигрыш игрока А равен проигрышу игрока В. Таким образом, рассматривается игра с нулевой суммой. В этой ситуации достаточно анализировать функцию выигрышей только одного из игроков. Пусть это будет игрок А.

     Функцию выигрышей игрока А можно записать в виде таблицы, в которой строки соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В.

	В1	…	Вs	…	Вn
А1	а11	…	а1s	…	а1n
…	….	…	…	…	…
Аk	аk1	…	аks	…	аkn
…	…	…	…	…	…
Аm	аm1	…	аms	…	аmn

 

Эта таблица  называется матрицей выигрышей игрока А или платежной матрицей игры. Платежная матрица игры – это табличная форма записи функции выигрыша. Элемент матрицы, стоящий на пересечении выбранных строки и столбца, определяет выигрыш игрока А.

При определении наилучших стратегий игроков основой рассуждений является принцип, который предполагает, что противники, участвующие в игре, одинаково разумны, и каждый из них делает все для того, чтобы добиться своей цели.

Целью игроков является выбор наиболее выгодных стратегий, доставляющих игроку А максимальный выигрыш, а игроку В – минимальный проигрыш.

Игрок А при выборе своей стратегии должен учитывать, что игрок В может ответить той своей стратегией, при которой выигрыш игрока А будет минимальным. Поэтому игрок А анализирует свои стратегии и определяет для каждой из них минимально возможный выигрыш, который он получит независимо от того, как поведет себя игрок В. Среди минимальных выигрышей он выбирает наибольшее значение и соответствующую стратегию считает наиболее предпочтительной. Таким образом, он рассчитывает величину a по формуле (14.1)

             (14.1)

a называется нижней ценой игры или максимином, а соответствующая ему стратегия – максиминной. a показывает величину минимального гарантированного выигрыша, который игрок А может получить, применяя рациональные стратегии при любых действиях игрока В [1].

Игрок В при выборе своей оптимальной стратегии должен учитывать, что игрок А может ответить той своей стратегией, при которой проигрыш игрока В будет максимальным. Поэтому для каждой своей стратегии игрок В определяет величину максимального проигрыша. Среди максимальных значений выбирается минимальное и соответствующая ему стратегия считается предпочтительной. Таким образом игрок В рассчитывает величину b по формуле:

                  (14.2)

b - верхняя цена игры или минимакс, а соответствующая стратегия игрока В называется минимаксной. Верхняя чистая цена игры показывает, какой максимальный проигрыш получит игрок В, если будут использоваться оптимальные стратегии или какой максимальный выигрыш игрок В позволит получить игроку А.

Таким образом, используя чистые стратегии, игрок А обеспечивает выигрыш не меньше a, а игрок В в результате применения своих чистых стратегий может не позволить игроку А выиграть больше чем b.

Пример 14.1.  Каждый из игроков независимо друг от друга записывает одну из цифр: 4,5,6. Если сумма записанных цифр оказалась четная, ее выигрывает игрок А, если нечетная – игрок В. Представим данную ситуацию в виде матричной игры двух лиц с нулевой суммой.

Решение.   У каждого из игроков имеется три стратегии:

· Первая стратегия – записать цифру 4,

· Вторая стратегия – записывать цифру 5,

· Третья стратегия – записывать цифру 6.

Построим матрицу выигрышей:

		В1(4)	В2(5)	В3(6)
	А1(4)	8	-9	10
А=	А2(5)	-9	10	-11
	А3(6)	10	-11	12

 

Так как у нас игра с нулевой суммой, то выигрыш одного игрока равен проигрышу другого, поэтому в платежной матрице выигрыш игрока В (нечетная сумма чисел, стоящих в соответствующих строке и столбце)  записывается с обратным знаком.

Рассчитаем верхнюю и нижнюю цены игры.

Для расчета нижней цены игры в каждой строке найдем наименьшее значение выигрыша игрока А, а затем среди наименьших выберем наибольшее. Результаты запишем в соответствующий столбец таблицы.

Для расчета верхней цены игры в каждом столбце найдем наибольший проигрыш игрока В, затем среди наибольших значений выберем наименьшее. Результаты запишем в соответствующую строку. (рис. 14.2).

 

	В1(4)	В2(5)	В3(6)	Α
А1(4)	8	-9	10	-9
А2(5)	-9	10	-11	-11
А3(6)	10	-11	12	-11
b	10	10	12

 

Итак, нижняя цена игры α=-9, верхняя цена игры b=10. Максиминная стратегия игрока А -  это стратегия А₁. Применяя ее, игрок А выиграет не менее -9. Применяя другие стратегии, он может получить меньший выигрыш.

Минимаксная стратегия игрока В – это одна из стратегий В₁ или В₂. Применяя их, игрок В гарантированно проиграет не более 10.

 

Особый частный случай рассматривается  в теории игр, когда нижняя цена игры равна верхней цене

a=b.                                  (14.3)

В этом случае говорят, что игра имеет седловую точку и цену игры n = a = b .

Обозначим через i* номер стратегии, соответствующей a, через j* -номер стратегии, соответствующей b.

Пару чистых стратегий, соответствующих i* , j*  называют седловой точкой матричной игры (A_i*, B_j*), а элемент a_i*j*-седловым элементом [7].

Седловой элемент является наименьшим в строчке и наибольшим в соответствующем столбце.

                          (14.4)

При этом выполняется равенство:

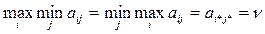
Если игра имеет седловую точку, то эта точка образует оптимальное решение игры, которое будем записывать так:

Решение, соответствующее седловой точке, обладает следующими свойствами:

1) Если обе стороны придерживаются своих оптимальных стратегий, то выигрыш игрока А (проигрыш игрока В) равен цене игры n

2) Если один из игроков придерживается своей оптимальной стратегии, а другой отклоняется от своей оптимальной стратегии, то для игрока, допустившего отклонение это не будет выгодным. Выигрыш игрока, допустившего отклонение, может либо остаться неизменным либо уменьшиться.

Пример 14.2.

Рассмотрим игру со следующей платежной матрицей:

Покажем, что данная игра имеет несколько седловых точек

Решение. Рассчитаем нижнюю и верхнюю цену игры

						α
	1	9	4	3	12	1
	2	4	6	5	8	2
	11	12	9	7	8	7
	15	8	7	2	12	2
	11	12	8	7	7	7
β	15	12	9	7	12

 

 Таким образом:

α=β=7

оптимальными стратегиями игрока А являются стратегии А₃ и А₅, оптимальной стратегией игрока В является стратегия В₄.

Оптимальным решением игры являются следующие седловые точки:

(А₃, В₄, v=7) и (А₅, В₄, v=7).

 

 Смешанные стратегии игроков и их свойства. В ситуации, когда игра не имеет седловой точки, используя принцип минимакса можно установить пределы, в которых будет находиться выигрыш игрока А (проигрыш игрока В). Тогда при многократном повторении игры, используя различные комбинации стратегий, игрок А может увеличить свой выигрыш, а игрок В – уменьшить свой проигрыш. Такая комбинация стратегий определяет смешанную стратегию.

Смешанной стратегией игрока А называется набор вероятностей =(p₁,p₂,…p_n) , с которыми игрок А применяет свои чистые стратегии при многократном повторении игры.  Этот набор вероятностей обладает следующими свойствами:

1.

2.

Аналогично смешанной стратегией игрока В называется набор вероятностей, =(q₁,q₂,…q_m), с которыми игрок В применяет свои чистые стратегии при многократном повторении игры. Набор вероятностей  обладает следующими свойствами:

1.

2.

 

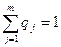
Очевидно, что каждая чистая стратегия является частным случаем смешанной стратегии, в которой вероятность применения данной стратегии равна единице, а остальные вероятности равны нулю [5].

Смешанные стратегии имеет смысл использовать при выполнении следующих условий:

• анализируемая игра не имеет  седловой точки;

• игроки используют случайную смесь чистых стратегий с заданными вероятностями;

• игра многократно повторяется в сходных условиях;

• при каждом из ходов ни один игрок не информирован о выборе стратегии другим игроком;

• допускается осреднение результатов игр.

Рассмотрим, как определяется функция выигрыша для игры в смешанных стратегиях.

Предположим, что в ходе игры с платежной матрицей А размерностью m´n игрок использует свою чистую стратегию B_i с вероятностью q_i. Тогда, учитывая независимость выбора игроками своих чистых стратегий, можно утверждать, что вероятность выбора комбинации (A_i,B_j) будет равна произведению вероятностей p_iq_j. В таком случае величина выигрыша игрока А (или проигрыша игрока В) становится случайной и можно говорить лишь о среднем  ожидаемом выигрыше игрока А или математическом ожидании:

Функция  называется функцией выигрыша или платежной функцией. Как видно, функция выигрыша зависит от самой смешанной стратегии, то есть от набора вероятностей, с которыми игроки принимают свои чистые стратегии.

Для смешанной стратегии введем  понятие нижней и верхней цены игры.

Стратегии  называются оптимальными смешанными стратегиями соответственно игроков А и В, если для любых смешанных стратегий 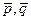 имеет место неравенство:

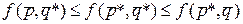
Основная теорема матричных игр   (теорема фон Неймана) утверждает, что любая конечная игра двух лиц с нулевой суммой имеет решение в смешанных стратегиях. [1]

Легко показать что цена игры находится между нижней ценой игры α и верхней ценой игры β:

Более того, для оптимальных смешанных стратегий справедливо соотношение:

Значение платежной функции при оптимальных смешанных стратегиях называют ценой игры.

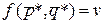
Решить игру – значит найти тройку

 

Для того, чтобы рассчитать оптимальные смешанные стратегии игроков, введем понятие активных чистых стратегий.

Итак, активными стратегиями называются чистые стратегии игрока, входящие в оптимальную стратегию с положительной вероятностью, называются активными стратегиями. Чистые стратегии, входящие в оптимальную стратегию с нулевой вероятностью, называются пассивными стратегиями.

Справедлива теорема:

Теорема об активных стратегиях. Для любой активной стратегии А_i игрока А выполняется равенство:

 f(A_i, )=v,

а для любой активной стратегии игрока В выполняется равнство:

f( , B_j)=v

Другими словами, если один из игроков действует по своей оптимальной смешанной стратегии, то выигрыш не изменяется и остается равным цене игры при условии, что второй игрок придерживается своих активных стратегий [7].

Критерий решения матричных игр Для того, чтобы смешанные стратегии  и  игры с матрицей (a_ij)_mn и ценой v были оптимальными необходимо и достаточно, чтобы выполнялись условия:

таким образом, если игрок А, использует свою оптимальную смешанную стратегию. а игрок В – любую чистую стратегию, то выигрыш игрока А при многократном повторении игры будет не меньше цены игры.

Если игрок В пользуется своей смешанной стратегией, а игрок А использует чистые стратегии, то проигрыш игрока В при многократном повторении игры будет не больше цены игры.

Этот критерий используется для обоснования решения матричной игры.

Прежде чем решать игру, если есть возможность, надо упростить платежную матрицу, исключив заведомо невыгодные стратегии игроков (доминируемые и дублируемые).

Если все элементы k-ой строки платежной матрицы не меньше соответствующих элементов s-ой строки , то k-ая строка является доминирующей s-ая строка – доминируемой и ее можно исключить из матрицы, так как стратегия a_s не выгодна игроку А, т.е. p_s=0.

Если все элементы l-го столбца не больше соответствующих элементов r-го столбца, то есть , то столбец b_l - доминирующий, b_r – доминируемый и его можно вычеркнуть из платежной матрицы, т.е. q_r=0.

Если все элементы k-ой строки равны соответствующим элементам s-го столбца, то такие строки (столбцы) называются дублирующими и одну (один) из них надо вычеркнуть из платежной матрицы.

Кроме того, можно показать, что если все элементы платежной матрицы умножить на любое положительное число z>0, то смешанные стратегии от этого не изменятся, а цена игры возрастет в это же количество раз .

Также, если ко всем элементам платежной матрицы прибавить одно и то же число с, то смешанные стратегии от этого не изменятся, а цена игры увеличится на это число .

 

Сведение матричной игры к задаче линейного программирования.

Рассмотрим игру с платежной матрицей (a_ij)_mn, i = 1, 2, .., m; j = 1, 2, , n.

все элементы которой неотрицательны, , α≠β (то есть нет седловой точки) и  ценой игры v, v>0.

Предположим, игрок А использует свою оптимальную смешанную стратегию, а игрок В применяет свои чистые стратегии, тогда  в зависимости от стратегии В_j игрока В средний выигрыш игрока А равен:

,

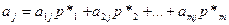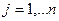
(т.е. элементы j-го столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий A₁ , A₂ , ..., A_m и результаты складываются).

В соответствии с критерием решения матричных игр все средние выигрыши игрока А будут не меньше цены игры.

,

 

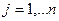
Каждое из неравенств можно разделить на число v > 0.

Введем новые переменные: x₁ = p₁/v, x₂ = p₂/v , ..., x_m= p_m/v    

Тогда система примет вид:

a_1jx₁+ a_2jx₂ + ...+ a_{m j}x_m  ≥ 1, j=1,2,…,n                 

 

Цель игрока А — максимизировать цену игры v.

Разделив равенство p₁+p₂+ ...+p_m = 1 на v ≠ 0, получаем, что переменные x_i (i = 1, 2, ..., m) удовлетворяют условию:

x₁+ x₂ + ...+ x_m = 1/v.

Максимизация цены игры v эквивалентна минимизации величины 1/v, поэтому задача может быть сформулирована следующим образом: определить значения переменных x_i ≥ 0, i = 1,2,...,m, так, чтобы они удовлетворяли линейным ограничениям (1) и при этом линейная функция 

Z = x₁+ x₂ + ...+ x_m

обращалась в минимум:

 

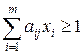
Таким образом, получим задачу линейного программирования в симметричном виде для игрока А.

Для определения оптимальной смешанной стратегии игрока В будем учитывать, что игрок В стремится уменьшить цену игры, то есть найти максимум функции . Если игрок В применяет свою оптимальную смешанную стратегию, а игрок А использует чистые стратегии, то в соответствии с критерием решения матричных игр переменные q*₁,…q*_m должны удовлетворять неравенствам

,

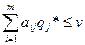Введем переменные y_j = q_j/v, j =1,2,...,n, 

Тогда:

a_1jy₁+ a_2jy₂ + ...+ a_{m j}y_n  ≤ 1, j=1,2,…,n                                                                        

Переменные y_j (j=1,2,...,n) удовлетворяют условию:

y₁+ y₂ + ...+ y_n = 1/v

Игра свелась к следующей задаче: определить значения переменных y_j ≥ 0, j=1,2,...,n, которые удовлетворяют системе неравенств (2) и максимизируют линейную функцию

Z' = y₁ + y₂ + ...+ y_n.

Решение полученной задачи линейного программирования:

y₁+ y₂ + ...+ y_n = 1/v (max)

a_1jy₁+ a_2jy₂ + ...+ a_{m n}y_n  ≤ 1, j=1,2,…,n

y_j ≥ 0, j = 1,2,...,n

определяет оптимальную стратегию Q*_B = (q*₁ + q*₂ + ...+ q*_n) .

Таким образом, получаем пару двойственных задач. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно-двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности.