 |
Главная |
Использование метода многокритериальной оценки в решении задач выбора альтернатив в условиях определенности
|
из
5.00
|
В данном пункте рассматривается метод многокритериальной оценки для простейшего случая, когда каждую отдельно взятую альтернативу можно оценить конкретным числом (значением критерия), и сравнение альтернатив сводится к сравнению соответствующих им чисел. В данной постановке экономические задачи встречаются наиболее часто. Например, при ранжировании хозяйствующих субъектов (альтернатив) 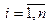 по совокупности показателей их финансово-хозяйственной деятельности
по совокупности показателей их финансово-хозяйственной деятельности 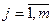 , при построении рейтинга логистических посредников (альтернатив)
, при построении рейтинга логистических посредников (альтернатив) 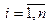 по совокупности критериев
по совокупности критериев 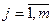 . Также данные методы реализуются в виде комплексов комптьютерных программ при создании системы поддержки принятия решений.
. Также данные методы реализуются в виде комплексов комптьютерных программ при создании системы поддержки принятия решений.
Несмотря на то, что решаемые экономические задачи различны, метод их решения единый - многокритериальные оценки. В соответствии с особенностями метода многокритериальной оценки, сущность которого концептуально изложена в п.9.1 происходит сведение множества критериев (целей) в единый критерий (цель) на основе использования различного рода сверток. Алгоритм использования метода для рассматриваемого варианта включает четыре последовательных шага: экономическое обоснование выбора критериев, их количественное представление и нормирование; ранжирование показателей-критериев; построение свертки и расчет интегрального показателя. Далее рассмотрим каждый шаг отдельно.
Экономическое обоснование выбора критериев и их количественное представление в виде показателей. В зависимости от объекта набор количественных и качественных критериев, формирующий интересующие качества объекта рейтингования изменяется. Например в соответствие с [10], при построении рейтинга (оценка одного объекта или субъекта относительно другого) логистических посредников (поставщиков) в качестве системы критериев выделяют набор показателей - цену продукции, надежность поставок, финансовое положение, время исполнения заказа, качество продукции, репутация в отрасли, оформление товара, соответствие продукции стандартам; при ранжировании перевозчиков рассматривают - надежность времени доставки, тарифы доставки «от двери до двери», общее время транзита, готовность перевозчика к переговорам об изменении тарифа, финансовая стабильность перевозчика, наличие оборудования по грузопереработке, наличие дополнительных услуг по комплектации и доставке груза, потери и хищение груза, экипирование отправок, квалификация персонала, отслеживание отправок, готовность схем маршрутизации перевозок, сервис на линии, процедура заявки транспортировки. Во многих исследованиях, наиболее часто связанных с оценкой эффективности объекта, строят многоуровневую систему показателей, где на верхнем уровне в агрегированном виде представлены критерии (например, экономический, социальный, экологический и др.), а на нижнем уровне данные критерии представлены в виде системы экономических показателей. Следует отметить, что систему показателей можно классифицировать в три группы: количественные, качественные и релейные. Для определения значений количественныхпоказателей 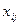
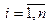
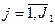 (например, цена продукции, финансовое положение) используются различные источники информации (отчеты, справочники, результаты опросов и т.п.), некоторые из показателей могут быть получены с участием экспертов. Качественные показатели
(например, цена продукции, финансовое положение) используются различные источники информации (отчеты, справочники, результаты опросов и т.п.), некоторые из показателей могут быть получены с участием экспертов. Качественные показатели 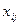
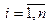
 (например, надежность поставки, качество продукции), как правило, оцениваются экспертно и выражаются лингвистическими переменными, которые могут быть представлены различным количеством состояний (термами): например, тремя состояниями («очень хорошо», «удовлетворительно», «очень плохо»), пятью ( «очень хорошо», «хорошо», «удовлетворительно», «плохо», «очень плохо») или семью («отлично», «очень хорошо», «хорошо», «удовлетворительно», «плохо», «очень плохо», «скверно»). К релейным показателям
(например, надежность поставки, качество продукции), как правило, оцениваются экспертно и выражаются лингвистическими переменными, которые могут быть представлены различным количеством состояний (термами): например, тремя состояниями («очень хорошо», «удовлетворительно», «очень плохо»), пятью ( «очень хорошо», «хорошо», «удовлетворительно», «плохо», «очень плохо») или семью («отлично», «очень хорошо», «хорошо», «удовлетворительно», «плохо», «очень плохо», «скверно»). К релейным показателям 
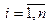
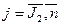 (например, соответствие стандартам, наличие специального оборудования) отнесены такие, которые имеют только два значения: «да», «нет», которым соответственно присваиваются значения 1 и 0.
(например, соответствие стандартам, наличие специального оборудования) отнесены такие, которые имеют только два значения: «да», «нет», которым соответственно присваиваются значения 1 и 0.
В соответствии с методикой расчета многокритериальных оценок исходные данные, представленные в виде матрицы значений j -го показателя  для i –й альтернативы
для i –й альтернативы 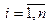 -
- 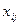 , приводят к сопоставимому безразмерному виду («нормализуют»). Обеспечение сопоставимости требует представления показателей в единой шкале, например, на отрезке [0,1]. Методики нормирования для количественных и качественных показателей. Рассмотрим каждую методику в отдельности.
, приводят к сопоставимому безразмерному виду («нормализуют»). Обеспечение сопоставимости требует представления показателей в единой шкале, например, на отрезке [0,1]. Методики нормирования для количественных и качественных показателей. Рассмотрим каждую методику в отдельности.
Обработка матрицы данных 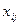
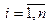
 , включающих
, включающих  количественных показателей , предусматривает следующие этапы:
количественных показателей , предусматривает следующие этапы:
· в зависимости от влияния показателя на общую оценку определяется эталонное значение оцениваемого показателя:
для позитивного показателя:

|
для негативного показателя:
 ; ;
|
· проводится нормирование показателя 
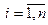 ,
,  . Существуют различные варианты нормирования показателей. Например, может быть применен следующий способ, по которому безразмерная величина критериев определяется по формуле:
. Существуют различные варианты нормирования показателей. Например, может быть применен следующий способ, по которому безразмерная величина критериев определяется по формуле:
 , ,
| (9.12) |
или:
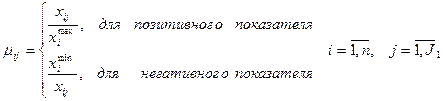 . .
| (9.13) |
Методика нормирования качественных показателей 
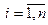
 состоит в преобразовании лингвистической переменной в безразмерную величину
состоит в преобразовании лингвистической переменной в безразмерную величину 
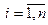 ,
,  на единичном отрезке [0,1] с использованием шкалы желательности, назначение которой состоит в установлении соответствия между физическими и психологическими параметрами.
на единичном отрезке [0,1] с использованием шкалы желательности, назначение которой состоит в установлении соответствия между физическими и психологическими параметрами.
Для этих целей может использоваться линейная шкала, согласно которой самая низкая оценка качественного показателя принимается за 0, а самая высокая – за 1. Шкала может быть аналитически описана в виде линейной функции желательности, представлен на рис. 9.4. Линейный характер функции желательности на рисунке приведен условно и может быть интерпретирован следующим образом: каждое последующее значение показателя x предпочтительнее предыдущего.
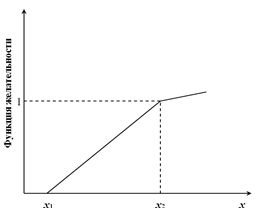
Рис. 9.3. Линейная функция желательности
Однако линейное преобразование имеет много недостатков, и главное из них – оно противоречит реально существующему нелинейному характеру зависимости безразмерного индекса с оценкой значения показателя. Поэтому в качестве альтернативы линейной функции желательности можно выбрать психофизическую шкалу Харрингтона [11]. Аналитически шкала описывается в виде функции
 ,
,
где  - значение лингвистической переменной на кодированной шкале.
- значение лингвистической переменной на кодированной шкале.
Графически функция желательности Харрингтона для случая лингвистической переменной с семью термами: «скверно»((-3)-(-2)), «очень плохо» ((-2)-(-1)), «плохо» ((-1)-0), «удовлетворительно» (0-1), «хорошо» (1-2), «очень хорошо»( 2-3), «отлично» (3-4), - представлена на рис. 9.4.

Рис.9.4. Функция желательности Харрингтона с семью термами
В таблицах 9.2 и 9.3 приведены значения функции желательности Харрингтона соответственно для случаев представления лингвистической переменной семью и пятью термами.
Таблица 9.2 Оценки качества и соответствующие им стандартные оценки на шкале желательности для случая представления лингвистической переменной семью термами
| Интервал | Лингвистическая оценка | Отметки на шкале желательности | |
| диапазон | среднее значение функции желательности | ||
| 3-4 | Отлично | Более 0,951 | 0,967 |
| 2-3 | Очень хорошо | 0,873 – 0,951 | 0,912 |
| 1-2 | Хорошо | 0,692 – 0,873 | 0,783 |
| 0-1 | Удовлетворительно | 0,368 – 0,692 | 0,530 |
| (-1)-0 | Плохо | 0,066 – 0,368 | 0,217 |
| (-2)-(-1) | Очень плохо | 0,001 – 0,066 | 0,033 |
| (-3)-(-2) | Скверно | Менее 0,001 | 0 |
Такой сигмоидальный характер зависимости желательности от величины показателя отвечает интуитивным представлениям об осторожном подходе к оценке крайних состояний.
Таблица 9.3 Оценки качества и соответствующие им стандартные оценки на шкале желательности для случая представления лингвистической переменной пятью термами
| Лингвистическая оценка (термы лингвистической переменной) | Интервалы значений функции желательности |
| Очень плохо | 0,00-0,20 |
| Плохо | 0,20-0,37 |
| Удовлетворительно | 0,37-0,63 |
| Хорошо | 0,63-0,80 |
| Очень хорошо | 0,80-1,00 |
Ранжирование показателей-критериев. Одним из главных вопросов в многокритериальных оценках является информация об относительной важности критерия. Результатом решения вопроса является определение весовых коэффициентов показателей  (
(  ). Эта процедура выполняется с привлечением эксперта.
). Эта процедура выполняется с привлечением эксперта.
При ранжировании наиболее часто используют следующие методы.
Непосредственная оценка – это метод измерения, который представляет собой процедуру выставления показателям- критериям числовых значений важности в виде количества баллов в рамках задаваемого диапазона. В этом случае весовой коэффициент  определяется как отношение оценки важности показателя к сумме оценок важности всех показателей.
определяется как отношение оценки важности показателя к сумме оценок важности всех показателей.
Парное сравнение – это метод измерения, при котором характеристики объектов сравниваются экспертами попарно для установления более предпочтительного объекта в каждой паре. Таким образом, данный метод, в отличие от ранжирования, имеющего ограничения по количеству оцениваемых объектов, может применяться для сколь угодно большого числа пар объектов. Сравнение только двух объектов (вместо всех сразу, как при непосредственной оценке) – значительно более простая задача для экспертов. Этот метод может быть применен также в том случае, когда различия между объектами слишком малы, чтобы было возможно их прямое ранжирование.
Суть метода парных сравнений состоит в следующем. На основе парного сравнения критериев по определенному правилу формируется матрица парных сравнений, на основе которой рассчитывается собственный вектор; если после нормализации вектор удовлетворяет требованиям согласованности, то его используют для определения весовых коэффициентов показателей.
Приведем далее основные сведения, минимально необходимые для практического использования метода парных сравнений.
Для установления относительной важности критериев используется шкала сравнений, состоящая из нечетных чисел от 1 до 9. Выбор данной шкалы определяется тем, что способность человека производить качественные разграничения хорошо представлена пятью определениями: равный (1); слабый (3); сильный (5); очень сильный (7); абсолютный (9).
Сравнения критериев задаются в виде матриц парных сравнений  , где m –количество критериев. Матрица состоит из элементов
, где m –количество критериев. Матрица состоит из элементов 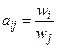 , показывающих соотношение значимостей i-ого критерия
, показывающих соотношение значимостей i-ого критерия  по сравнению со значимостью j-го критерия
по сравнению со значимостью j-го критерия  . Матрица парных сравнений имеет вид:
. Матрица парных сравнений имеет вид:
 .
.
Диагональные элементы матрицы равны единице, т.к. 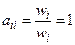 . Для любых i и k справедливо равенство
. Для любых i и k справедливо равенство  . Матрица А является обратно-симметричной. В качестве обратно-симметричной можно привести матрицу
. Матрица А является обратно-симметричной. В качестве обратно-симметричной можно привести матрицу 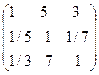 . Она соответствует перечисленным выше свойствам.
. Она соответствует перечисленным выше свойствам.
Матрица А называется согласованной, если при любых i, k и l имеет место равенство 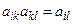 . Таким образом, идеальная матрица парных сравнений – обратно-симметричная и согласованная. Справедливо следующее утверждение [9].
. Таким образом, идеальная матрица парных сравнений – обратно-симметричная и согласованная. Справедливо следующее утверждение [9].
Утверждение 9.1. Положительная обратно-симметричная матрица является согласованной тогда и только тогда, когда порядок матрицы и ее наибольшее собственное значение совпадают:  .
.
Максимальное собственное значение вычисляется по формуле  , где
, где  – единичный вектор-строка , А – матрица парных сравнений, W – собственный вектор матрицы А.
– единичный вектор-строка , А – матрица парных сравнений, W – собственный вектор матрицы А.
Процедура определения собственных векторов матриц поддается приближению. Существует несколько способов приближенного вычисления собственного вектора обратно-симметричной матрицы. Рассмотрим один из них.
1) суммируются элементы каждой строки и полученные результаты записываются в столбец;
2) складываются все элементы найденного столбца;
3) каждый из элементов этого столбца делится на полученную сумму.
Если  , то в качестве степени отклонения положительной обратно-симметричной матрицы от согласованной можно взять отношение
, то в качестве степени отклонения положительной обратно-симметричной матрицы от согласованной можно взять отношение
 .
.
Это отношение называется индексом однородности. Показателем однородности суждений является отношение однородности
 ,
,
где М(ИО) – среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений, которое основано на экспериментальных данных (табл. 9.4)
Таблица 9.4. Среднее значение индекса однородности в зависимости от порядка матрицы
|
| Порядок матрицы (m) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| М(ИО) | 0,00 | 0,00 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 |
В качестве допустимого используется значение OO ≤ 0,10. Если для матрицы парных сравнений отношение однородности OO > 0,10, то это свидетельствует о существенном нарушении логичности суждений, допущенном экспертом при заполнении матрицы, поэтому эксперту предлагается пересмотреть данные, использованные для построения матрицы, чтобы улучшить однородность.
Пример 9.2. Рассматривается три критерия: А1 – качество, А2 – цена, А3 - время, для которых построена матрица парных сравнений
Таблица 9.5. Матрица парных сравнений примера 9.2.
| А1 | А2 | А3 | |
| А1 | 1 | 1 | 3 |
| А2 | 1/3 | 1 | 1/3 |
| А3 | 1/3 | 3 | 1 |
Требуется определить весовые коэффициенты критериев (проранжировать критерии).
Решение. Вначале рассчитаем собственный вектор матрицы парных сравнений
Таблица 9.6 Построение вектора приоритетов для критерия «Цена сырья»
| Цена | А1 | А2 | А3 | Сумма элементов строки | Вектор приоритетов 
|
| А1 | 1 | 1 | 3 | 5 | 5 / 11,67 = 0,43 |
| А2 | 1 | 1 | 1/3 | 5 | 5 / 11,67 = 0,43 |
| А3 | 1/3 | 3 | 1 | 1,67 | 1,67 / 11,67 = 0,14 |
| Сумма | 11,67 | 1 | |||
Максимальное собственное значение матрицы парных сравнений
 .
.
Матрица является согласованной, т.к.  .
.
Естественно, что индекс однородности и среднее значение индекса однородности равны нулю. Определим среднее значение индекса однородности для матрицы третьего порядка в табл. 9.4:  . Отношение однородности
. Отношение однородности  .
.
Следовательно, весовые коэффициенты критериев А1, А2, А3 составляют соответственно  =0,43;
=0,43; 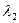 =0,43;
=0,43; 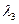 =0,14.
=0,14.
Выбор функции свертки и расчет интегрального показателя. Интегральный показатель наиболее часто описывается в виде аддитивной свертки:
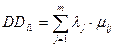 ; (9.14)
; (9.14)
либо мультипликативной
 . (9.15)
. (9.15)
Вариант DDi2 обладает свойством компенсации малых значений одних критериев за счет других. Например, если один из критериев-показателей равен 0, то и интегральный показатель  нулевой. Такая свертка удобна при принятии решений в том случае, если низкие значения ни по одному критерию недопустимы. Если низкие значения по отдельным критериям допускаются, то в этом случае можно использовать критерий
нулевой. Такая свертка удобна при принятии решений в том случае, если низкие значения ни по одному критерию недопустимы. Если низкие значения по отдельным критериям допускаются, то в этом случае можно использовать критерий  .
.
Если все критерии имеют одинаковый вклад, то можно использовать критерии равномерной оптимальности, т.е. λ i = 1/n и соотношения (9.14), (9.15) перепишутся в виде:
 , ,
| (9.16) | |
 . .
| (9.17) |
Пример 9.3. Провести рейтинговую оценку поставщиков и выбор лучшего поставщика на основе представленных в таблице 9.7 значений критериев. При выборе поставщика требуется обеспечить выполнение условия соответствия стандартам.
Таблица 9.7 Показатели для оценки поставщиков
| Критерий | Поставщики | ||||
| А | Б | В | Г | ||
| 1 | Цена продукции (руб./ед.) | 100 | 110 | 95 | 88 |
| 2 | Надежность поставок | 0,86 | 0,95 | 0,85 | 0,8 |
| 3 | Финансовое положение | 8 | 7 | 6 | 7 |
| 4 | Время исполнения заказа | 5 | 6 | 4 | 5 |
| 5 | Качество продукции | Очень хорошее | Очень хорошее | Хорошее | Очень хорошее |
| 6 | Репутация в отрасли | Хорошая | Очень хорошая | Удовлетво-рительная | Хорошая |
| 7 | Оформление товара | Очень хорошее | Отличное | Хорошее | Очень хорошее |
| 8 | Соответствие продукции стандартам | Да | Да | Да | Нет |
Решение. Из таблицы видно. Что показатели разделены на количественные (1 – 4), качественные (5 – 7) и релейные (8).
В соответствии с алгоритмом после проверки ограничений поставщик Г, продукция которого не соответствует международным стандартам качества, исключается из дальнейших расчетов. Следует отметить, что поставщики могут быть исключены из рассмотрения в случае отклонения количественных и качественных показателей за установленные пределы. Например, если надежность выполнения поставок окажется ниже 0.7, то такой поставщик исключается из рассмотрения.
Приведем качественные показатели 5 – 7 к количественному виду, используя функцию желательности Харрингтона (табл. 9.2). В результате показатели для оценки поставщиков будут представлены в таблице в количественном выражении (табл. 9.8).
Таблица 9.8 Количественное выражение показателей для оценки поставщиков
| Критерий | Поставщики | |||
| А | Б | В | ||
| 1 | Цена продукции (руб./ед.) | 100 | 110 | 95 |
| 2 | Надежность поставок | 0,86 | 0,95 | 0,85 |
| 3 | Финансовое положение | 8 | 7 | 6 |
| 4 | Время исполнения заказа | 5 | 6 | 4 |
| 5 | Качество продукции | 0,912 | 0,912 | 0,783 |
| 6 | Репутация в отрасли | 0,783 | 0,912 | 0,53 |
| 7 | Оформление товара | 0,912 | 0,967 | 0,783 |
Далее проведем нормирование показателей в соответствии, например, с формулой ( 9.12) :
Таблица 9.9 Нормирование критериев
| Критерий | Поставщики | |||
| А | Б | В | ||
| 1 | Цена продукции (руб./ед.) | 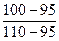
| 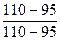
| 
|
| 2 | Надежность поставок | 
| 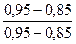
| 
|
| 3 | Финансовое положение | 
| 
| 
|
| 4 | Время исполнения заказа | 
| 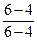
| 
|
| 5 | Качество продукции | 
| 
| 
|
| 6 | Репутация в отрасли | 
| 
| 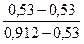
|
| 7 | Оформление товара | 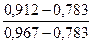
| 
| 
|
Также будем учитывать, что критерии имеют разную направленность. При выборе поставщиков критерии 1, 4 минимизируются, т.е. являются негативными, а все остальные критерии позитивные. Поэтому после нормировки критерии 1, 4 умножаются на (-1): это обеспечит максимизацию всех критериев (табл. 9.10).
Таблица 9.10 Нормированные значения критериев выбора поставщиков
| Критерий | Поставщики | |||
| А | Б | В | ||
| 1 | Цена продукции (руб./ед.) | -0,333 | -1 | 0 |
| 2 | Надежность поставок | 0,1 | 1 | 0 |
| 3 | Финансовое положение | 1 | 0,5 | 0 |
| 4 | Время исполнения заказа | -0,5 | -1 | 0 |
| 5 | Качество продукции | 1 | 1 | 0 |
| 6 | Репутация в отрасли | 0,662 | 1 | 0 |
| 7 | Оформление товара | 0,701 | 1 | 0 |
Для определения интегрального показателя определим приоритеты критериев, построив матрицу парных сравнений.
Таблица 9.11 Матрица парных сравнений для критериев
| Критерии | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Сумма | Приоритет |
| 1 | 1 | 1 | 1/3 | 1 | 1/5 | 1 | 1 | 5,53 | 5,53/73,0,5=0,075 |
| 2 | 1 | 1 | 1/3 | 1 | 1/5 | 1 | 1 | 5,53 | 0,075 |
| 3 | 3 | 3 | 1 | 3 | 1/3 | 3 | 3 | 16,33 | 0,22 |
| 4 | 1 | 1 | 1/3 | 1 | 1/5 | 1 | 1 | 5,53 | 0,075 |
| 5 | 5 | 5 | 3 | 5 | 1 | 5 | 5 | 29 | 0,4 |
| 6 | 1 | 1 | 1/3 | 1 | 1/5 | 1 | 1 | 5,53 | 0,075 |
| 7 | 1 | 1 | 1/3 | 1 | 1/5 | 1 | 1 | 5,53 | 0,075 |
| Сумма: | 73,0 | 1 | |||||||
Для матрицы парных сравнений (табл. 9.11) критерий «Финансовое положение», немного значительнее всех критериев, кроме критерия «Качество продукции», последнему он немного уступает; критерий «Качество продукции» значительнее всех критериев и немного значительнее критерия «Финансовое положение»; важность критерия «Цена продукции» сопоставима с критериями «Надежность поставок», «Время исполнения заказа», «Репутация в отрасли» и т.д. Просуммируем элементы построенной матрицы по строкам и нормируем их, в результате получим приоритет для каждого критерия (табл. 9.11).
Максимальное собственное значение матрицы парных сравнений рассчитывается
 .
.
Для оценки согласованности матрицы рассчитаем индекс однородности 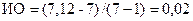 , определим среднее значение индекса однородности для матрицы седьмого порядка в табл. 9.4:
, определим среднее значение индекса однородности для матрицы седьмого порядка в табл. 9.4: 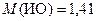 . Отношение однородности
. Отношение однородности 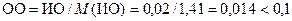 , что указывает на удовлетворительный результат.
, что указывает на удовлетворительный результат.
Следовательно, весовые коэффициенты критериев в нашей задачи составляют соответственно  =
= 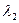 =
=  =
=  =
=  =0,075;
=0,075;  =0,22;
=0,22;  =0,4.
=0,4.
Оценим интегральный показатель как среднее взвешенное, используя формулу (9.16):
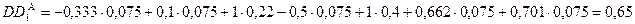 аналогично рассчитываем
аналогично рассчитываем
 ,
,
 .
.
Наибольшее значение свертки критериев имеет поставщик А, следовательно, основываясь на методе аддитивного свертывания, следует отдать предпочтение первому поставщику. Используя данный метод, необходимо помнить, что решение зависит от весовых коэффициентов, т.е. изменение веса может привести к другому результату.
Вопросы для контроля знаний
1. Приведите формальное описание многокритериальной задачи линейной оптимизации.
2. Дайте определение множества Парето.
3. Что такое замещающая задача и в чем принцип ее формирования?
4. Какие известны методы решения многокритериальных задач?
5. Охарактеризуйте методы решения многокритериальной оптимизации, основанные на свертывании критериев.
6. Охарактеризуйте метод нахождения арбитражных решений для задач многокритериальной оптимизации.
7. Охарактеризуйте методы идеальной точки для решения задач многокритериальной оптимизации.
8. Охарактеризуйте метод последовательных уступок для решения задач многокритериальной оптимизации.
9. Опишите методику построения многокритериальных оценок для решения задачи выбора альтернатив в условиях определенности.
10. Опишите методику нормирования количественных показателей.
11. Опишите методику нормирования качественных показателей. Определите понятие функции желательности.
12. Охарактеризуйте методики ранжирования критериев.
13. Что такое матрица парных сравнений. Охарактеризуйте методику ее построения.
14. Приведите условия согласованности матрицы парных сравнений.
15. Приведите вид аддитивной свертки.
16. Приведите вид мультипликативной свертки.
[1] Вектор-функция это вектор, компонентами, которого являются функции.
[2] Подмножество K из Rn называется конусом, если 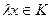 для всех
для всех 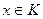 и любого числа
и любого числа  .
. 
[3] В 2007 г. группа 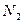 включала черную, цветную металлургию и топливную промышленность.
включала черную, цветную металлургию и топливную промышленность.
|
из
5.00
|
Обсуждение в статье: Использование метода многокритериальной оценки в решении задач выбора альтернатив в условиях определенности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

