Глава 9. Многокритериальные методы и экономико-математические модели в условиях определенности

 

В практической деятельности часто встречаются задачи, заключающиеся в поиске лучшего (оптимального) решения при наличии различных критериев оптимизации. Эти критерии обычно противоречивы в том смысле, что не существует решения, наилучшего одновременно по каждому из них. Такого рода задачи могут быть сформулированы как задачи выбора наилучшей альтернативы при заданном наборе критериев и ограничений. Многокритериальные задачи выбора альтернатив чрезвычайно многообразны: множество альтернатив может быть конечным, счетным или конти­нуальным; критерии могут иметь как коли­чественный, так и качественный характер; режим выбора может быть однократным (разовым) или повторяю­щимся, допускающим обучение на опыте; последствия выбора могут быть точно известны (выбор в условиях определенности), иметь вероятностный характер (выбор в усло­виях риска), или иметь неоднозначный исход, не допускающий введения вероятностей (выбор в условиях неопределенности); и т.д. Различные сочетания перечисленных вариантов и приводят к много­образным задачам выбора, которые изучены не в одинаковой степени.

Целью раздела является изложение наиболее простых и часто используемых в условиях определенности методов и моделей линейной многокритериальной оптимизации  и метода многокритериальной оценки для случая, когда каждую отдельно взятую альтернативу можно оценить конкретным числом (значением критерия), и сравнение альтернатив сводится к сравнению соответствующих им чисел.

Более подробно с данными вопросами можно ознакомиться в литературе [1-10].

 

9.1. Многокритериальные методы: основные понятия

Впервые задача многокритериальной (векторной) оптимизации возникла у итальянского экономиста В.Парето (V.Pareto, 1848-1923) при математическом исследовании процесса рыночного обмена товаров. Позже аналогичные задачи появились и в других областях.

Основные определения. Важнейшим понятием многокритериальной теории является понятие оптимальности по Парето. Оно представляет собой обобщение понятия точки максимума числовой функции на случай нескольких функций: решение оптимально по Парето, если значение любого из критериев можно улучшить лишь за счет ухудшения значений хотя бы одного из остальных критериев.

Основы теории многокритериальной оптимизации были заложены в работах К.Эрроу, Х.Куна, Т.Саати, А.Таккера, Т.Купманса, С.Карлина и др. в начале 50-х гг. 20 века.

Пусть задано множество альтернатив . На этом множестве определены n скалярных функций , представляющих собой критерии оценки качества альтернатив. Задача состоит в максимизации вектор-функции[1]

на множестве Х, т.е. в максимизации каждой компоненты вектора f(x) на множестве Х. Такую задачу будем обозначать через (X, f).

Если нужно минимизировать функцию f_i(x), то такая задача сводится к задаче на максимум путем замены f_i(x) на .

Отметим еще, что любой критерий f_i можно заменить на kf_i+l (где k>0), a^fi (a>1), b ^{- fi} (0<b<1) или на  (с – нечетное положительное число). Если критерий f_i положителен на Х, то вместо него можно взять , а неотрицательный критерий f_i можно преобразовать в . Указанные преобразования широко применяются к критериям в обычных экстремальных задачах [3].

Задачи, в которых критерии упорядочены по важности (и перенумерованы) так, что каждый предыдущий несравненно важнее, чем все последующие, называются лексикографическими задачами оптимизации. В таких задачах следует добиваться сколь угодно малого приращения более важного критерия за счет сколь угодно больших потерь по всем остальным менее важным критериям.

В зависимости от структуры множества Х и свойств функций 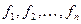 для удобства исследования выделяют различные классы многокритериальных задач. Так, если множество Х содержит конечное число элементов, то задача называется конечной, а если Х исчислимо, т.е. конечно или же счетно, то – дискретной. В частности, если у каждого вектора х из Х все компоненты x_i – целые числа, то задача называется целочисленной. А если векторы, образующие множество Х, булевы, т.е. состоят из нулей и единиц, то и сама задача называется булевой.

Если Х выпукло, а все f_i – вогнутые функции, то задача называется вогнутой. В частности, если Х – полиэдральное множество, т.е. «вырезано» из Rⁿ конечной системой линейных неравенств и равенств, а все f_i – линейны, то многокритериальная задача называется линейной.

Сущность многокритериальной задачи (X, f) состоит в нахождении оптимального ее решения, т.е. такого , которое в том или ином смысле максимизирует значения всех функций 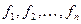. Так как существование решения, максимизирующего все целевые функции, является редким исключением, то обычно приходится стараться увеличивать значение каждого критерия, насколько это возможно. Поэтому в теории многокритериальной оптимизации понятие оптимальности получает различные и притом нетривиальные истолкования.

Будем говорить, что альтернатива  доминирует по Парето над альтернативой , если выполняются неравенства

,

причем среди этих неравенств имеется хотя бы одно строгое. Это означает, что выбор х¹, а не х² позволяет каждому критерию получить не меньшее значение, а хотя бы по одному – строго большее. Те альтернативы из множества Х, для которых не существует доминирующих альтернатив, называются эффективными или оптимальными по Парето. Иначе говоря, альтернатива  называется эффективной или оптимальной по Парето, если не существует такой альтернативы , что

,

и хотя бы для одного i это неравенство строгое.

Из данного определения вытекает, что улучшение по какому-либо критерию относительно альтернативы, оптимальной по Парето, может быть достигнуто только за счет ухудшения по какому-нибудь иному критерию.

Множество всех оптимальных по Парето альтернатив для задачи (X, f) будем обозначать через Р(X, f) и называть множеством Парето.

Важнейшая особенность задачи многокритериальной оптимизации состоит в том, что ее решением является, как правило, не единственная точка, а множество Парето, представленное неэквивалентными и содержательно существенно разными решениями. В однокритериальных задачах в качестве оптимального можно брать любое решение, максимизирующее критерий (поскольку все они эквивалентны).

В многокритериальной задаче каждая альтернатива  полностью характеризуется ее векторной оценкой . Если альтернатива х пробегает все множество Х, то в пространстве векторных оценок Rⁿ образуется множество F=f(X), которое будем называть множеством векторных оценок. Поэтому выбор оптимальных по Парето альтернатив сводится к выбору оптимальных по Парето векторных оценок. Множество всех оптимальных по Парето векторных оценок будем обозначать через P(F).

В случаях наличия лишь двух или трех критериев множество P(F) можно изобразить графически. Поэтому при анализе двух-, а иногда и трехкритериальных задач нередко удобнее всего выбирать оптимальное по Парето решение непосредственно на основе рассмотрения графика множества P(F).

Для иллюстрации рассмотрим простейший пример с двумя критериями. Пусть множество векторных оценок  в координатах f₁ и f₂ имеет вид, изображенный на рис. 9.1.

Рис. 9.1. Множество векторных оценок

Легко видеть, что множество векторных оценок, доминирующих по Парето векторную оценку f(x), совпадает с неотрицательным ортантом (конусом[2]) C(x), вершина которого перенесена в точку f(x). В самом деле, для любой точки  имеем , причем, если , то хотя бы одно неравенство будет строгим. Поэтому на рис. 9.1 векторная оценка f(x) (или, что то же самое, альтернатива х) не является оптимальной по Парето, поскольку каждая точка из множества , отличная от f(x), доминирует по Парето оценку f(x).

Базовые методы решения многокритериальных задач можно подразделить на следующие группы: методы, основанные на свертывании критериев; метод нахождения арбитражных решений; метод идеальной точки; метод последовательных уступок.

Вместо исходной многокритериальной задачи в соответствии с выбранным методом, формируется замещающая задача. В состав замещающей задачи входит один критерий, а к исходной системе ограничений добавляется одно или несколько дополнительных ограничений. Решение замещающей задачи должно принадлежать области Парето, т.е. быть эффективным.

Широко известным подходом к решению многокритериальной задачи (X, f) является метод многокритериальной оценки, в рамках которой происходит сведение многокритериальной задачи к обычной («однокритериальной») задаче математического программирования путем замены целевых функций  на одну «составную» функцию . В ее роли могут выступать «взвешенные суммы» («линейная свертка») , «взвешенные минимумы»  и др. «свертки» исходных целевых функций. Здесь l _i некоторые отрицательные числа, называемые коэффициентами важности. Они характеризуют не только относительную важность критериев, но и приводят критерии разной размерности к безразмерному сопоставимому виду. Такой подход концептуально и технически представляется самым удобным.

Одним из самых ответственных и сложных этапов построения обобщенных критериев является определение коэффициентов важности. Обычно для их определения приходится использовать специальную информацию, запрашиваемую у лица, принимающего решение, или получаемую от эксперта.

Вначале все исходные критерии , приводят к сопоставимому безразмерному виду  («нормализуют»). Чаще всего используют такие преобразования:

1) ;

2) ,

где  - некоторое «эталонное» (максимально возможное), а  - минимально возможное значение критерия .

Далее все критерии  «сворачивают» в одну функцию – обобщенный критерий F(l, f), учитывая их относительную важность при помощи специальных положительных чисел . Здесь .

Частный случай данного подхода заключается в выборе главного критерия, т.е. в том, чтобы все веса l _i, за исключением некоторого , полагать равными нулю. Тогда многокритериальная задача перейдет в однокритериальную задачу, а множество ее оптимальных решений можно рассматривать как множество допустимых решений новой многокритериальной задачи с целевыми функциями .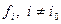

Один из вариантов описанного подхода состоит в том, что исходная многокритериальная задача (x, f) сводится к задаче оптимизации по одному критерию  [3], который объявляется главным, при условии, что значения всех остальных критериев должны быть не меньше некоторых установленных величин («требуемых уровней», «пороговых значений» и т.п.) t_i, т.е. к задаче

.

Дж.Нэшем (J.Nash) предложен метод нахождения так называемых арбитражных решений [4], существенно ограничивают число выбираемых решений среди оптимальных по Парето. Его идея состоит в установлении на основании содержательных соображений некоторых минимальных допустимых значений  и в последующем нахождении допустимых х, максимизирующего

.

В [3] для задачи (x, f) предлагается использовать метод идеальной точки, состоящий в нахождении такой точки множества Парето, векторная оценка которой находится ближе всего к идеальной точке 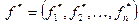. Под идеальной точкой здесь понимается такая точка, координаты которой представляют собой оптимальные значения  целевых функций соответствующих однокритериальных задач. Когда мы говорим о нахождении точки «ближайшей к идеальной», мы предполагаем, что в пространстве векторных оценок введена некоторая метрика. В [4] для измерения отклонения используется метрика

,

где  - значение i-го критерия на решении х,  - i-ая координата идеальной точки, р – некоторое положительное число .

Хотя метод идеальной точки представляется очень привлекательным, он не лишен довольно существенных недостатков. В самом деле, метрику в Rⁿ можно вводить различными способами, а при разных метриках наилучшими могут оказываться разные оптимальные по Парето решения. Можно показать, что для любого оптимального по Парето решения найдется метрика, в которой векторная оценка этого решения будет ближайшей к идеальной точке. Итак, от задачи выбора оптимального по Парето решения приходим к задаче выбора метрики, которая отнюдь не проще.

В [3] для решения многокритериальной задачи предлагается использовать  метод последовательных уступок. Суть метода состоит в том, что критерии нумеруются в порядке убывания важности. Далее в соответствии с рейтингом решается однокритериальная задача

на основе определяется оптимальное значение критерия  и  экспертом устанавливается  уступка  по первому критерию. Далее решается задача по следующему критерию в рейтинге с дополнительно введенным ограничением

Если в задаче более двух критериев, то процедура повторяется для других критериев.

Далее приведем примеры решения задач многокритериальной оптимизации.

Пример 9.1. Предприятие может производить продукцию двух видов П₁ и П₂, используя для этого два вида ограниченных ресурсов Р₁ и Р₂. Расход ресурсов на производство продукции, запасы ресурсов и прибыль приведены в таблице 9.1.

Таблица 9.1

Ресурс	Расход ресурса на 1 т продукции		Количество ресурса
	П1	П2
Р1	1	2	80
Р2	6	2	240
Прибыль, ден.ед.	10	35

Определить план производства продукции, максимизирующий прибыль и суммарное количество продукции.

Необходимо решить задачу:

1. Методом последовательных уступок, если более важным является критерий прибыли и уступка по нему составляет 175 ден.ед.

2. Методом идеальной точки, исходя из того, что целевое значение показателя прибыли составляет , а объема выпуска –   и значение p=2.

3.  Методом многокритериальной оценки  при .

4. Методом арбитражных решений, если минимальные допустимые значения для критериев .

Решение.

Построим математическую модель задачи. Обозначим через х₁ и х₂ количество продукции вида П₁ и П₂ соответственно. Тогда модель задачи

Для определения множества Парето сделаем графическую иллюстрацию (рис. (9.2))

Рис. 9.2. Область допустимых решений и оптимальные решения по двум критериям

В точке А с координатами (0; 40) значение  первой целевой функции максимально и составляет 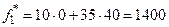. Максимальная прибыль равна 1400 ден. ед. и достигается при выпуске 40 т продукции второго вида.

В точке В с координатами (32; 24) вторая целевая функция достигает максимума, ее значение равно 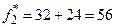, то есть максимальный выпуск продукции составляет 56 т при выпуске 32 т продукции первого вида и 24 т второго. Отрезок АВ есть область Парето (область компромисса) решение задачи должно принадлежать этой области.

 

1. Решим задачу методом последовательных уступок.

Уступка по критерию прибыли составляет 175 ден. ед. Дополнительное ограничение замещающей задачи формируется в соответствии с неравенством  и для данной задачи имеет вид

,

тогда замещающая задача примет вид

Решением задачи является  х₁ = 23,3; x₂ = 28,3; f₂= 23,3 + 28,3 = 51,6; f₁ = 10 ∙ 23,3 + + 35 ∙ 28,8 = 1225. Полученное решение является эффективным, т.к. точка (23,3; 28,3) расположена на отрезке АВ.  Таким образом, при выпуске 22,3 т продукции первого вида и 28,3 т продукции вто­рого вида прибыль составит 1225 ден. ед., объем выпуска – 51,6 т.

2. Решим задачу методом идеальной точки. Запишем модель замещающей задачи

Получим решение

Поскольку отклонения от оптимальных величин критериев ненормированы, то решение приближено к максимальному значению первого критерия т.к. масштаб этого показателя больше.  Пронормируем отклонения, разделив их на максимальные значения функций, чтобы привести отклонения критериев  к сопоставимому и безразмерному виду

Решение: . Оба полученных решения эффективны.

3. Решим задачу методом аддитивной свертки. Модель  замещающей задачи

Решение: . - точка максимума функции объема выпуска.

 Если изменить значения весовых коэффициентов и принять . Модель замещающей задачи

 

Получим решение .   - точка максимума функции прибыли. Недостатком метода является чувствительность решения изменениям весовых коэффициентов.  Множество Парето в рассматриваемой задаче является отрезком. Решением, полученным по методу линейной свертки может быть либо точка А либо точка Б. При малейшем изменении значений весовых коэффициентов решение существенно изменяется.

4. Решим задачу методом арбитражных решений. Модель замещающей задачи

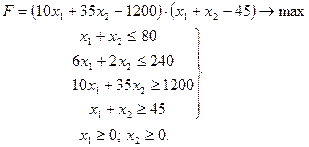
Решение: . Решение эффективно.