Лабораторная работа №4. Решение задачи целочисленного программирования

 

1. Записать задачу целочисленного программирования.

2. Решить задачу методом Гомори.

Задача целочисленного программирования приводится к каноническому виду.

       Модуль Gomori;

    Входные данные:

– m – число ограничений;

– n  – число переменных;

– С – вектор коэффициентов целевой функции;

– А – матрица коэффициентов системы ограничений и правых частей (ввод построчный);

Выходные данные:

– х – вектор целочисленныых значений оптимального решения;

– z –оптимальное значение целевой функции.

 

    Пример.

    f =5x₁ + 4x₂ max

1x₁ + 1x₂+1x₃ =18

5x₁ - 1x₂ + 1x₄=20

1x₁ - 1x₂ +1x₅ =8

 

Текст программы.

 

Program Gomori;

uses crt;

var

f1,f2: text;

a : array[1..100,0..100] of real;

c,b : array[1..100] of real;

d : array[0..100] of real;

k : array[0..100] of byte;

kt,kt2,dl: integer;

i,j,m,n,mi,mj,r,x,y : byte;

dj,min,max : real;

s : string[12];

st,s1,s2,s3 : string[10];

ch : char;

 

{ВЫВОД В ФАЙЛ ЧИСЛА В ФОРМАТЕ}

procedure wr(r:real;b:boolean);

var w: byte;

begin

if (abs(frac(r)-round(frac(r)))>0.0001) or (r>1.0e10) then str(r:4:2,st)

else str(round(r),st);

if b then for w:=length(st) to 10 do st:=st+' ';

write(f2,st);

end;

 

{ВЫВОД В ФАЙЛ ТАБЛИЦ}

procedure writetablefile;

var ws:string[10];

begin

writeln(f2,#10,#13,' ИТЕРАЦИЯ______',kt2,'.',kt);

if s='' then dl:=79 else dl:=n*12;

for i:=1 to dl do write(f2,'=');

write(f2,#10,#13,'bx ');

for i:=0 to n do

begin

if (s='') and (i>6) then break;

if (abs(frac(c[i])-round(frac(c[i])))>0.2) or (c[i]>1.0e10)

  then str(c[i]:4:2,st) else str(round(c[i]),st);

str(i,ws);

st:='a'+ ws + '=' + st;

for j:=length(st) to 11 do st:=st+' ';

write(f2,st);

end;

writeln(f2);

for i:=1 to dl do write(f2,'-');

for i:=1 to m do

begin

write(f2,#10, #13, 'x', k[i], ' ');

if (s='') and (i>15) then break;

for j:=0 to n do

   begin

   if (s='') and (j>6) then break;

   wr(a[i,j],true);

   end;

end;

writeln(f2);

for i:=1 to dl do write(f2,'-');

write(f2,#10,#13,'z: ');

for j:=0 to n do

begin

if (s='') and (j>6) then break;

wr(d[j],true);

end;

writeln(f2);

for i:=1 to dl do write(f2,'=');

end;

 

{ПЕРЕСЧЕТ ПО ПРАВИЛУ ПРЯМОУГОЛЬНИКА (ЖОРДАН-ГАУСС)}

procedure gauss;

begin

for i:=1 to m do

for j:=0 to n do

   if (i<>mi) and (j<>mj) then

      a[i,j]:=a[i,j]-a[mi,j]*a[i,mj]/a[mi,mj];

for i:=1 to m do if i<>mi then a[i,mj]:=0;

d[mj]:=0;

for j:=0 to n do a[mi,j]:=a[mi,j]/min;

end;

 

{СИМПЛЕКС МЕТОД}

procedure simplex;

begin

for i:=1 to m do

begin

{ЗАНОСИТСЯ НОМЕР БАЗИСНОЙ ПЕРЕМЕННОЙ И ЕЕ НОМЕР}

for j:=n downto 1 do if a[i,j]<>0 then

  begin

  b[i]:=c[j]; k[i]:=j; break;

  end;

end;

 

r:=0;

{ПЕРЕСЧЕТ z}

repeat

for j:=0 to n do

begin

dj:=0;

for i:=1 to m do dj:=dj+b[i]*a[i,j];

d[j]:=dj-c[j];

end;

writetablefile;

inc(kt);

min:=0;mj:=0;

{ВЫБОР НАПРАВЛЯЮЩЕГО СТОЛБЦА}

for j:=1 to n do

if min>d[j] then begin min:=d[j]; mj:=j; end;

if mj=0 then break;

mi:=0; min:=1.7e38;

{ВЫБОР НАПРАВЛЯЮЩЕЙ СТРОКИ}

for i:=1 to m do

if (a[i,mj]>0) and (min>a[i,0]/a[i,mj]) then

  begin

  min:=a[i,0]/a[i,mj];

  mi:=i;

  end;

if mi=0 then begin r:=2; break; end;

min:=a[mi,mj];

gauss;

b[mi]:=c[mj];

writeln(f2,#13,#10,' x',k[mi],'=>x',mj);

k[mi]:=mj;

if s2='con' then if s='' then ch:=readkey;

until ch=#27;

end;

 

{ДВОЙСТВЕННЫЙ СИМПЛЕКС МЕТОД}

procedure doublesimplex;

begin

r:=0;

repeat

writetablefile;

inc(kt);

min:=0;

{ВЫБОР НАПРАВЛЯЮЩЕЙ СТРОКИ}

for i:=1 to m do if min>a[i,0] then begin min:=a[i,0]; mi:=i; end;

if min=0 then break;

min:=1.7e38;

{ВЫБОР НАПРАВЛЯЮЩЕГО СТОЛБЦА}

for j:=1 to n do if a[mi,j]<-0.001 then

begin

dj:=-d[j]/a[mi,j];

if min>dj then begin min:=dj; mj:=j; end;

end;

if min=1.7e38 then begin r:=2; writetablefile; break; end;

min:=a[mi,mj];

b[mi]:=c[mj];

writeln(f2,#10,#13,' x',k[mi],'=>x',mj);

k[mi]:=mj;

gauss;

for j:=0 to n do

begin

dj:=0;

for i:=1 to m do begin

dj:=dj+b[i]*a[i,j];

delay(1); end;

d[j]:=dj-c[j];

end;

if s2='con' then if s='' then ch:=readkey;

until ch=#27;

end;

 

{ВЫВОД РЕЗУЛЬТАТА Х=( ) }

procedure result;

var res:byte;

begin

if r=2 then write(f2,#13,#10,'Нет решения !')

 else begin

write(f2,#13,#10,' x=( ');

for i:=1 to n do

     begin

     res:=0;

     for j:=1 to m do if k[j]=i then res:=j;

     if res<>0 then begin wr(a[res,0],false); write(f2,'; '); end

        else write(f2,' 0;');

     end;

writeln(f2,')');

write(f2,' z= '); wr(d[0],false);

end;

     writeln(f2);

     writeln(f2,' ');

     write(f2,' .В.');

 

end;

 

procedure klv;

begin

writeln('Введите число ограничений и число переменных+число ограничений');

read(m); readln(n);

writeln('Задача вводится в канонической форме !');

writeln('Введите заданные коэффициенты целевой функции');

for i:=1 to n do read(c[i]);

writeln('Введите известные коэффициенты в системе ограничений');

writeln(' и произвольные коэффициенты по-строчно');

for i:=1 to m do begin

                      for j:=1 to n do read(a[i,j]);

                         read(a[i,0]);

                 end; readln;

end;

 

procedure fil;

begin

writeln('Введите имя исходного файла');

readln(s1);

{ОТКРЫТИЕ ИСХОДНОГО ФАЙЛА }

{$i-}

if s1='' then

begin

     writeln('Ошибка открытия файла !');

     writeln('Не задано имя !')

end

else

begin

     assign(f1,s1);

     reset(f1);

     read(f1,m); readln(f1,n);

     for i:=1 to n do read(f1,c[i]);

     for i:=1 to m do begin

                           for j:=1 to n do read(f1,a[i,j]);

                           read(f1,a[i,0]);

                      end;

     close(f1);

end;

end;

 

{=======================================================}

 

begin

clrscr;

writeln('Ввод исходных данных ''0''-с клавиатуры, ''1''-из файла');

readln(s3);

if s3='0'then klv;

if s3='1' then fil;

 

writeln('Введите имя файла для записи результата или ''con'' для вывода на экран');

readln(s2);

 

if s2='' then writeln('НЕ ЗАДАНО УСТРОЙСТВО ВЫВОДА !')

else

begin

     assign(f2,s2);

     rewrite(f2);

     clrscr;

     {ПРОВЕРКА НА ПРАВИЛЬНУЮ КАНОНИЧЕСКУЮ ФОРМУ}

     for i:=1 to m do if a[i,0]<0 then

         begin

              write('НЕ ПРАВИЛЬНАЯ КАНОНИЧЕСКАЯ ФОРМА !');

              readkey;

              exit;

         end;

 

     {ВЫВОД В ФАЙЛ ЗАДАЧИ}

     writeln(f2,'РАЗМЕРНОСТЬ ЗАДАЧИ - ',m,'x',n);

     write(f2,' ');

     for i:=1 to n do

     begin

          if (c[i]>0) and (i=1) then begin wr(c[i],false); write(f2,'x',i); end;

          if (c[i]>0) and (i>1) then begin write(f2,'+'); wr(c[i],false); write(f2,'x',i); end;

          if c[i]<0 then begin wr(c[i],false); write(f2,'x',i); end;

     end;

     writeln(f2,' =>max');

     for i:=1 to m do

     begin

          write(f2,i,') ');

          for j:=1 to n do

          begin

               if (a[i,j]>0) and (j=1) then begin wr(a[i,j],false); write(f2,'x',j); end;

               if (a[i,j]>0) and (j>1) then begin write(f2,'+'); wr(a[i,j],false); write(f2,'x',j); end;

               if a[i,j]<0 then begin wr(a[i,j],false); write(f2,'x',j); end;

          end;

          write(f2,'='); wr(a[i,0],false); writeln(f2);

     end;

     if s2='con' then if s='' then ch:=readkey;

     if ch=#27 then exit;

     kt:=0; kt2:=0;

     simplex;

     if ch=#27 then exit;

     result;

     if r=2 then

     begin

          if s2='con' then if s='' then readkey;

          close(f2);

          exit;

     end;

     if s2='con' then if s='' then ch:=readkey;

     if ch=#27 then exit;

     {МЕТОД ГОМОРИ}

     repeat

           r:=0;

           inc(kt2);

           for i:=1 to m do if abs(a[i,0]-round(a[i,0]))>0.0001 then begin r:=1; break; end;

           if r=0 then

           begin

                close(f2);

                exit;

           end

           else writeln(f2,#10,#13,#10,' ПЕРЕМЕННЫЕ НЕЦЕЛОЧИСЛЕННЫЕ : ФОРМИРУЕМ ОТСЕЧЕНИЕ.');

           if (n+2)<102 then begin inc(n); inc(m); end

           else begin

                     write(f2, #13, #10, 'ОШИБКА : ПЕРЕПОЛНЕНИЕ !');

                     if s2='con' then if s='' then readkey;

                     close(f2);

                     exit;

           end;

           k[m]:=n;

           min:=50;

           for i:=1 to m-1 do if (abs(a[i,0]-round(a[i,0]))>0.0001) and (min>k[i]) then

           begin

                mi:=i;

                min:=k[i];

           end;

           for j:=0 to n-1 do if a[mi,j]>=0 then a[m,j]:=-frac(a[mi,j])

               else a[m,j]:=-(a[mi,j]+abs(int(a[mi,j]))+1);

           a[m,n]:=1;

           kt:=0;

           doublesimplex;

           if ch=#27 then exit;

           result;

           if s2='con' then if s='' then ch:=readkey;

     until ch=#27;

     close(f2);

end;

end.

 

Входные данные.

m=3

n=5

Вектор коэффициентов целевой функции

5 4 0 0 0

Матрица коэффициентов системы ограничений и ее правых частей построчно

1 1 1 0 0 18

5 -1 0 1 1 20

1 -1 0 0 1 8

 

Результаты расчета.

x=(6;12;0;2;14;0)

z=78.

 

Варианты заданий.

1 f(x)=x₁ + 2x₂  max (min)                        

2x₁ - x₂ 6                                          

2x₁ + x₂ 1

     

3 f(x)=x₁ + 3x₂ max (min)

  -x₁ + x₂ 6

 x₁ – 2x₂ ≥10

     

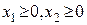
5 f(x)=x₁ + x₂ max (min)

   x₁ - 2x₂ 14

-5x₁ + 3x₂ 15

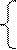7 f(x)=5x₁ + 7x₂ max (min)

5x₁ - 6x₂ 30

x₁ – 4x₂ 28

2 f(x)=3x₁ + 2x₂ max (min)

2x₁ + x₂ 12

x₁ + x₂ 1

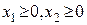
4 f(x)=3x₁ + x₂ max (min)

-x₁ - 2x₂ 8

-2x₁ + x₂ 2

 6 f(x)=-2x₁ - 3x₂ max (min)

-4x₁ + 2x₂ 4

x₁ - x₂ 6

  

8 f(x)=x₁ + x₂ max (min)

-2x₁ - x₂ 6

-x₁ + 3x₂ 9

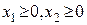
9 f(x)=x₁ + 3x₂ max (min)

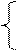-7x₁ + 4x₂ 28

x₁ - 3x₂ 15

11 f(x)=x₁ + 3x₂ max (min)

3x₁ + 4x₂ 12

2x₁ - x₂ 10

  

13 f(x)=2x₁+3x₂ max(min)

x₁ - 4x₂ 12

-4x₁ + x₂ 4

15 f(x)=3x₁ + x₂ max (min)

-7x₁ + 3x₂ 21

x₁ – 5x₂ 10

  

17 f(x)=3x₁ + x₂ max (min)

x₁ - 2x₂ 6

x₁ + 5x₂ 8

   

19 f(x)=2x₁ + x₂ max(min)

-2x₁ + x₂ 10

x₁ - x₂ 8

 

21 f(x)=5x₁ + 4x₂ max(min)

  x₁ - 5x₂ 20

-x₁ + x₂ 9

 

 10 f(x)=x₁+2x₂ max (min)

  x₁ - 6x₂ 6

-2x₁ + x₂ 2

12 f(x)=x₁ + 5x₂ max (min)

-x₁ - x₂ 12

x₁ - 4x₂ 8

  

14 f(x)=2x₁ + 3x₂ max (min)

x₁ + x₂ 10

2x₁ + x₂ 6

16 f(x)=3x₁+2x₂ max(min)

  4x₁ + 3x₂ ≤8

x₁ + x₂ 4

18 f(x)=x₁ + 4x₂ max (min)

2x₁ - 2x₂ 14

-x₁ - x₂ 6 

 

20 f(x)=x₁ + 3x₂ max (min)

x₁ - 2x₂ 6

-x₁ + 3x₂ 6

  

22 f(x)=x₁ - x₂ max (min)

2x₁ - 3x₂ 12

x₁ + x₂ 1

 

 23 f(x)=6x₁ + 2x₂ max (min)

-3x₁ + x₂ 6

-3x₁ + x₂ 1

x₁ + 4x₂ 28

25 f(x)=x₁+x₂ max (min)

3x₁ - 4x₂ 12

x₁ + x₂ 1

27 f(x)=6x₁ + x₂ max (min)

-x₁ + x₂ 15

x₁ - 3x₂ 9

 

28  f(x)=2x₁ + x₂ max (min)

x₁ + x₂ 2

x₁ + 2x₂ 8

3x₁ – x₂ 6

24 f(x)=2x₁ + x₂ max (min)

-x₁ + x₂ 1

x₁ – 2x₂ 1

x₁ – x₂ 8

 

26 f(x)=2x₁+x₂ max (min)

x₁ - 5x₂ 10

x₁ - 2x₂ 6

  

29  f(x)=4x₁ + x₂ max (min)

-6x₁ + x₂ 12

x₁ + 2x₂ 10

 

 30 f(x)=5x₁+2x₂ max (min)

x₁ - 3x₂ 9

3x₁ – x₂ 6

2x₂ 12