 |
Главная |
Цифровые модели элементов радиосистем, описываемых нелинейными дифференциальными уравнениями.
|
из
5.00
|
В большинстве случаев исследования радиосистем методами математического моделирования их можно описать дифференциальными уравнениями
Ψ(y,y',…,y(n),t,x,x',…,x(m),α,β)=0. (14)
Здесь x,x',…,x(m) и y,y',…,y(n) – входные и выходные фазовые переменные и их производные; t – независимая переменная – время; α, β – множества внешних и внутренних параметров системы; t=t0; y0=y(t0);  - начальные условия.
- начальные условия.
В процессе моделирования системы необходимо определить реакцию системы y(t) и её производные на некотором заданном интервале t0≤t≤TН.
В методах численного решения дифференциальных уравнений подобного вида используется принцип пошагового интегрирования, при котором начиная с начальных условий осуществляется предсказание последующих значений переменной y=y(t) и её производных.
Все алгоритмы численного решения дифференциальных уравнений можно разбить на одноступенчатые методы прогноза и многоступенчатые методы прогноза и коррекции. Одноступенчатые методы прогноза для получения решения в момент t1=t0+Δt используют информацию о начальных условиях, которые предполагаются заданными. Поэтому соответствующие алгоритмы являются самоначинающимися. Многоступенчатые методы прогноза и коррекции для получения решения в момент ti=t0+iΔt используют информацию о y=y(t) в некоторые предыдущие моменты времени ti-1, ti-2,…, т.е. для их реализации необходимо знать решения yi-1,  на предыдущих этапах. Это несамоначинающиеся численные алгоритмы. Такие алгоритмы более экономны в смысле затрат машинного времени при той же точности решения задачи.
на предыдущих этапах. Это несамоначинающиеся численные алгоритмы. Такие алгоритмы более экономны в смысле затрат машинного времени при той же точности решения задачи.
Особенностью численных методов решения дифференциальных уравнений является то, что они применимы для решения дифференциальных уравнений только 1-го порядка
 (15)
(15)
С начальными условиями t=t0, y=y0.
Если радиосистема описывается уравнением n-го порядка, то для численного решения его необходимо описать совокупностью уравнений 1-го порядка. Если решение такого уравнения существует и единственно, то его можно представить рядом Тейлора в окрестности точки ti

где при t=ti (i=1,2,…,K, K=TH/Δt)

 (16)
(16)
……………………………………………….
Несмотря на то, что этот алгоритм решения уравнения является самоначинающимся и сравнительно просто позволяет получить решение с любой точностью, с точки зрения возможности его реализации на ЭВМ он обладает существенным недостатком. Здесь для получения решения на каждом шаге t1, t2,…,tk необходимо вычислять производные  что приводит к значительным затратам машинного времени. Поэтому многие известные алгоритмы используют аппроксимацию конечного числа членов разложения решения в ряд Тейлора. При этом аппроксимация осуществляется так, чтобы отпала необходимость в вычислении производных в (16).
что приводит к значительным затратам машинного времени. Поэтому многие известные алгоритмы используют аппроксимацию конечного числа членов разложения решения в ряд Тейлора. При этом аппроксимация осуществляется так, чтобы отпала необходимость в вычислении производных в (16).
Наиболее часто применяемые при моделировании радиосистем алгоритмы представлены в табл. 1. Алгоритм Эйлера использует первые два члена разложения в ряд Тейлора, алгоритм Эйлера-Коши – три, а алгоритм Рунге-Кутта 4-го порядка - четыре. Наиболее точными из приведенных в табл. 1 являются алгоритмы Рунге-Кутта. Точность решения задачи в каждом отдельном случае зависит также от интервала Δt. Поэтому остановимся на принципах выбора интервала дискретизации Δt в зависимости от необходимой точности решения задачи.
Таблица 1.
| Метод численного решения | Цифровой алгоритм (модель) | Погрешность решения εi+1 | |
| на одном шаге | при 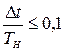
| ||
| Эйлера | 
| 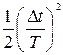
| 5·10-3 |
| Эйлера - Коши | 


| 
| 1,6·10-4 |
| Рунге-Кутта (4-го порядка) | 


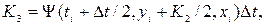

| 
| 8,33·10-8 |
Рассмотрим алгоритм цифрового моделирования инерционного звена

Соответствующее дифференциальное уравнение

Для произвольного внешнего воздействия x(t) алгоритм Эйлера дает следующее решение:
 (17)
(17)
Оценим точность решения задачи на одном шаге, полагая, что в системе имеет место только собственное движение (x=0). В этом случае  (t=t0, y=y0), и можно получить точное решение задачи
(t=t0, y=y0), и можно получить точное решение задачи

Из (17) получаем решение методом Эйлера

Относительная погрешность решения на одном шаге
 .
.
Если положить  , то
, то 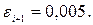 Погрешности решения аналогичной задачи на одном шаге методами Эйлера-Коши и Рунге-Кутта 4-го порядка, приведены в табл. 1.
Погрешности решения аналогичной задачи на одном шаге методами Эйлера-Коши и Рунге-Кутта 4-го порядка, приведены в табл. 1.

Лекцию разработал
Доцент к.т.н. доцент В. Ерохин
26.06.2014
|
из
5.00
|
Обсуждение в статье: Цифровые модели элементов радиосистем, описываемых нелинейными дифференциальными уравнениями. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

