 |
Главная |
Численные методы. Применение ЭВМ.
|
из
5.00
|
Численные методы. Применение ЭВМ.
9.73*. Определить коэффициенты  в выражениях для двух низших частот собственных колебаний
в выражениях для двух низших частот собственных колебаний 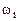 , при
, при 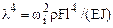 в случае балки постоянного сечения. Рассмотреть балку, защемленную по концам, используя метод конечных элементов на основе вариационного принципа. Принять в первом приближении число конечных элементов
в случае балки постоянного сечения. Рассмотреть балку, защемленную по концам, используя метод конечных элементов на основе вариационного принципа. Принять в первом приближении число конечных элементов  . В приведенной выше формуле EJ – жесткость балки, l – длина, p – плотность материала, F- площадь поперечного сечения. Сравнить результаты с точным решением.
. В приведенной выше формуле EJ – жесткость балки, l – длина, p – плотность материала, F- площадь поперечного сечения. Сравнить результаты с точным решением.
Решение:
Выписываем уравнение Лагранжа, как в решении задачи 7.84, считая статическую силу P и ее потенциал V равным нулю:
 ,
,
здесь T – кинетическая энергия системы

и U – потенциальная энергия
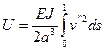 .
.
Напомним, что точка над буквой обозначает дифференцирование по времени, а штрих – по безразмерной координате 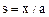 , где a – длина конечного элемента.
, где a – длина конечного элемента.
Пользуясь зависимостями и обозначениями, приведенными в решении задачи 7.84, где даны подробные выкладки, находим:
 ,
, 
Нетрудно видеть, что матрицы масс  и
и  будут совпадать с матрицами масс граничных элементов задачи 7.84:
будут совпадать с матрицами масс граничных элементов задачи 7.84:
 ,
,  .
.
Кинетическая энергия для системы в целом
 ,
,
где M – глобальная матрица масс для всего стержня. Она получается путем сложения соответствующих элементов матриц  и
и  :
:
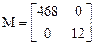 .
.
Потенциальная энергия для стержня (см. задачу 7.73)
 ,
,
где
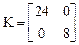 .
.
Подставляя T и U в уравнение (1) получим
 . (2)
. (2)
Решение уравнения (2) будем искать в виде
 , (3)
, (3)
где  - амплитуда колебаний,
- амплитуда колебаний, 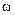 - собственная частота.
- собственная частота.
Подстановка (3) в уравнение (2) дает
 .
.
Учитывая, что  , перепишем это уравнение в виде
, перепишем это уравнение в виде
 .
.
Раскрывая определитель, получим
 .
.
откуда  и
и  .Сопоставление с точным решением дано в ответе.
.Сопоставление с точным решением дано в ответе.
9.74*. Решить предыдущую задачу для балки шарнирно опертой по концам, приняв  .
.
Решение:
В рассматриваемом случае
 ,
,  или
или  .
.
Так же, как в решении задачи 7.74, находим для элемента 1-2
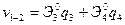 .
.
Для элемента 2-3
 .
.
Определим кинетическую энергию балки
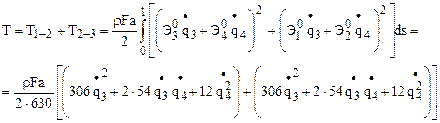
В матричной форме будет
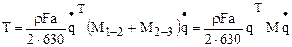
Здесь через  и
и  обозначены матрицы масс элементов 1-2 и 2-3, через М – матрица масс для всего стержня:
обозначены матрицы масс элементов 1-2 и 2-3, через М – матрица масс для всего стержня:
 ,
,  ,
,  .
.
Потенциальная энергия стержня (см. решение задачи 7.73):

Здесь
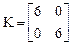 .
.
Далее
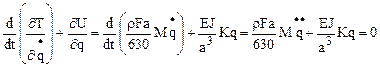 .
.
Задавая решение в виде  , будем иметь
, будем иметь

Учитывая, что  , приходим к уравнению
, приходим к уравнению
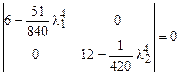 .
.
Отсюда  и
и  .Сопоставление с точным решением приведено в ответе.
.Сопоставление с точным решением приведено в ответе.
9.75*. Рассмотреть с помощью ЭВМ задачу 9.73, принимая число конечных элементов  , и определить пять низших частот в сравнении с точным решением.
, и определить пять низших частот в сравнении с точным решением.
Решение:
Используем решение задачи 7.84, считая статическую нагрузку Р=0.
Уравнение собственных колебаний стержня получает вид
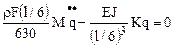 (1)
(1)
Выберем решение уравнения (1) в виде  . Тогда
. Тогда
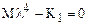 , (2)
, (2)
где  - вектор коэффициентов собственных частот колебаний стержня
- вектор коэффициентов собственных частот колебаний стержня
 ,
,  ,
,  .
.
Уравнение (2) можно привести к виду
 ,
,
где l – единичная матрица.
Таким образом, задача свелась к нахождению собственных значений матрицы  , которое можно осуществить на ЭВМ типа ЕС с помощью подпрограммы NROOT. Полученные таким образом значения первых пяти частот
, которое можно осуществить на ЭВМ типа ЕС с помощью подпрограммы NROOT. Полученные таким образом значения первых пяти частот 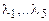 приведены в ответе в сопоставлении с точным решением.
приведены в ответе в сопоставлении с точным решением.
9.76*. Решить задачу 9.74, считая число конечных элементов  , и найти пять низших частот в сопоставлении с точным решением.
, и найти пять низших частот в сопоставлении с точным решением.
Решение:
По сравнению с предыдущей задачей изменятся лишь следующие элементы матрицы масс  и жесткости
и жесткости 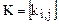 ,
,  ,
, 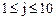 :
:
 ,
,  ,
,
 ,
,
 ,
,  ,
,
 .
.
Полученные таким же образом, как и в задаче 9.75, значения 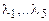 приведены в ответе в сравнении с точными значениями.
приведены в ответе в сравнении с точными значениями.
Численные методы. Применение ЭВМ.
7.73*. Определить коэффициент  в формуле для критической силы
в формуле для критической силы  в случае центрально сжатого стержня постоянного сечения, пользуясь методом конечных элементов на основе вариационного принципа. Представить прогиб отдельного участка – конечного элемента – в виде полинома
в случае центрально сжатого стержня постоянного сечения, пользуясь методом конечных элементов на основе вариационного принципа. Представить прогиб отдельного участка – конечного элемента – в виде полинома  , где
, где 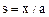 - безразмерная координата, отсчитываемая от одного из концов элемента, а – длина элемента. Рассмотреть случай защемленных концов стержня, принимая в первом приближении число конечных элементов n=2.
- безразмерная координата, отсчитываемая от одного из концов элемента, а – длина элемента. Рассмотреть случай защемленных концов стержня, принимая в первом приближении число конечных элементов n=2.
Указание. Эта и следующие две задачи могут быть решены без использования ЭВМ, как показано в решении.
Решение:
Основываясь на вариационном метода Ритца, вычисляем потенциальную энергию деформации стержня при выпучивании в пределах конечного элемента длины а и жесткости EJ:
 .
.
Пользуясь дифференциальным уравнением изогнутой оси

и вводя безразмерную координату 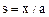 , приходим к выражению
, приходим к выражению
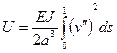 ; (1)
; (1)
Штрихи обозначают дифференцирование по s. Жесткость EJ считается в пределах конечного элемента постоянной. Отметим здесь же, что мы будем, по условию задачи, принимать жесткость постоянной и для всего стержня – ради простоты решения, хотя преимущество метода конечных элементов состоит в возможности учета произвольного закона изменения жесткости по длине стержня (см. задачу 7.83).
Далее определим изменение потенциала внешней нагрузки (См. Вольмир А.С. Устойчивость деформируемых систем.-М.:Наука, 1967, с.40)
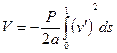 . (2)
. (2)
Заметим, что данный метод позволяет принять во внимание наличие внешних сил, приложенных в различных сечениях стержня (см. задачу 7.83). Здесь осевая сила считается постоянной по всей длине.
Прогиб стержня в пределах конечного элемента, по условию,
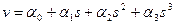 . (3)
. (3)
Введем индексы  для узлов, ограничивающих конечный элемент. Будем считать, что система n выбранных конечных элементов имеет 2n степеней свободы, отвечающих прогибам узлов
для узлов, ограничивающих конечный элемент. Будем считать, что система n выбранных конечных элементов имеет 2n степеней свободы, отвечающих прогибам узлов  ,
,  и углам поворота
и углам поворота  ,
,  и т. д.; под q понимаются обобщенные координаты. Имеем при
и т. д.; под q понимаются обобщенные координаты. Имеем при 
 и
и  ; при
; при 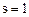
 и
и  . Определяя из этих условий коэффициенты
. Определяя из этих условий коэффициенты  , составим выражение для
, составим выражение для  . Получим
. Получим
 , (4)
, (4)
где
 ,
,  ,
,
 ,
, 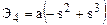 .
.
Эти функции носят названия эрмитовых. Каждый элемент может иметь свою длину а; в нашем изложении будем считать длины всех элементов одинаковыми. По условию стержень делится на два конечных элемента с узлами 1, 2, 3 и обобщенными координатами  . Так как в узлах 1 и 3 стержень защемлен, для этих узлов прогибы и углы поворота обращаются в нуль:
. Так как в узлах 1 и 3 стержень защемлен, для этих узлов прогибы и углы поворота обращаются в нуль:  ; в пределах первого элемента будет
; в пределах первого элемента будет 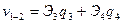 , в пределах второго элемента
, в пределах второго элемента  .
.
Потенциальная энергия элемента 1-2
 (5)
(5)
Перепишем это выражение в матричной форме:
 ,
,
где  - матрица жесткости элемента 1-2:
- матрица жесткости элемента 1-2:
 ,
, 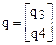 ,
,  .
.
Потенциальная энергия элемента 2-3:
 , (6)
, (6)
или
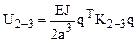 ;
;
здесь
 .
.
Для системы в целом потенциальная энергия
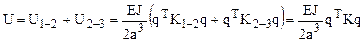 .
.
Матрица жесткости всего стержня К находится путем сложения соответствующих элементов матриц  и
и 
 , или
, или 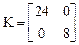 .
.
Изменение потенциала внешних сил по (2)
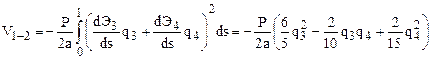 , (7)
, (7)
или
 ,
,
где  - матрица геометрической жесткости элемента 1-2:
- матрица геометрической жесткости элемента 1-2:
 .
.
Аналогично для  :
:
 , (8)
, (8)
где
 .
.
Для всего стержня
 .
.
Матрица геометрической жесткости всего стержня S также находится сложением соответствующих элементов  и
и  :
:
 или
или 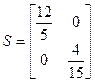 .
.
Исходя из вариационного принципа, записываем условие равновесия
 .
.
Здесь 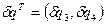 . Считая
. Считая  ,
,  , получим
, получим
 . (9)
. (9)
Нетривиальное решение (при  и
и 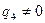 ) однородных уравнений (9) находим, приравнивая нулю определитель:
) однородных уравнений (9) находим, приравнивая нулю определитель:
 .
.
Отсюда при 
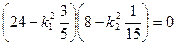 .
.
Окончательно получим два решения, последовательно приравнивая нулю выражения в скобках:
 ,
,  .
.
Найденный таким образом коэффициент критической силы – наименьшее собственное значение – сопоставляется в ответе с точным (аналитическим) решением.
7.74*. Решить задачу 7.73 для случая такого же стержня, но шарнирно опертого по концам.
Решение:
Используем путь, описанный в решении задачи 7.73. Но здесь надо учесть новые условия закрепления. Граничные условия для элемента 1-2 в узле 1 будут:  ,
,  . По первому из этих условий
. По первому из этих условий  . По второму условию, исходя из формулы (4) в решении задачи 7.73, получим:
. По второму условию, исходя из формулы (4) в решении задачи 7.73, получим:
 .
.
Следовательно,  . Подставляя
. Подставляя  , выраженное через
, выраженное через  ,
,  в (4) и приводя подобные члены имеем
в (4) и приводя подобные члены имеем
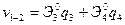 ,
,
где
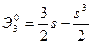 ,
,  .
.
Аналогично для элемента 2-3 при граничных условиях в узле 3  ,
,  получим:
получим:

где
 ,
,  .
.
Вычислим энергию деформации стержня по выражениям (1), (5) и (6) в решении задачи 7.73, но с новыми значениями  и т. д. Получим
и т. д. Получим
 ,
, 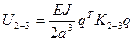 ,
,
где
 ,
,  ,
, 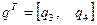 .
.
Для всего стержня
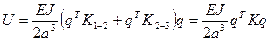 .
.
Здесь
 или
или  .
.
Аналогичным образом по выражениям (2) и (8) задачи 7.73 находим
 ,
,  . (1)
. (1)
Для стержня в целом
 . (2)
. (2)
Через  ,
,  , S в (1) и (2) обозначены следующие выражения:
, S в (1) и (2) обозначены следующие выражения:
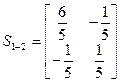 ,
,  ,
,  .
.
Таким образом. Решение задачи сводится, как и в задаче 7.73, к нахождению собственных значений определителя
 ,
,
или

Здесь учтено значение  . Находим
. Находим
 .
.
Отсюда  ,
,  . Соответствующий силе коэффициент
. Соответствующий силе коэффициент  выписан а ответе в сопоставлении с точным решением.
выписан а ответе в сопоставлении с точным решением.
7.75*. Рассмотреть задачу типа 7.73, считая один конец стержня шарнирно опертым, а второй – защемленным.
Решение:
Используя тот же путь, что и в предыдущих двух задачах, приходим к выражениям
 ,
,
 .
.
Здесь 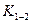 ,
,  определяется, как и в задаче 7.74, а
определяется, как и в задаче 7.74, а  ,
,  - как в задаче 7.73. Глобальные матрицы жесткости и геометрической жесткости имеют вид
- как в задаче 7.73. Глобальные матрицы жесткости и геометрической жесткости имеют вид
 ,
,  .
.
Так же как и в задаче 7.73, решение находится из уравнения

или при  и
и 
 .
.
Раскрывая определитель, приходим к уравнению
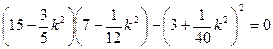 . (1)
. (1)
или  . Собственные значения задачи:
. Собственные значения задачи:  ,
,  .
.
Сравнение с точным решением см. в ответе.
7.76*. Пользуясь ЭВМ, решить задачу 7.73 в более высоком приближении, приняв число конечных элементов n=6.
Решение:
Функция прогиба для элемента 2-3 имеет вид

Выпишем это выражение в матричном виде
 ,
, 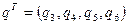 .
.
Матрица жесткости элемента 2-3

Для граничных элементов 1-2 и 6-7 матрицы жесткости (см. решение задачи 7.73):
 ,
,  .
.
Потенциальную энергию для стержня в целом получаем, последовательно сочетая матрицы жесткости для элементов 1-2, 2-3, 3-4 … 6-7:
 ,
, 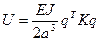 ,
,
где 
Полная матрица К является ленточной и имеет вид


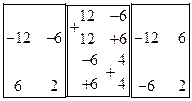
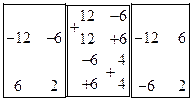

Вычислим изменение потенциала внешних сил для элемента, не примыкающего к концам стержня:

Выражение для  в матричной форме приобретает вид
в матричной форме приобретает вид
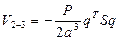 ,
,
где  ; под S понимается матрица геометрической жесткости, связанная с изменением потенциала внешних сил:
; под S понимается матрица геометрической жесткости, связанная с изменением потенциала внешних сил:
 .
.
Матрицы геометрической жесткости для элементов 1-2 и 6-7 имеют вид
 ,
,  .
.
Находим изменение потенциала внешних сил для всего стержня:
 ,
,
И здесь, последовательно сочетая матрицы жесткости для отдельных элементов, получаем:
 ,
,
где  ; ленточная матрица геометрической жесткости S для всего стержня имеет вид
; ленточная матрица геометрической жесткости S для всего стержня имеет вид


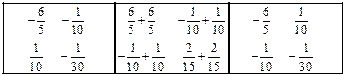


Решающее уравнение задачи при  ,
,  :
:
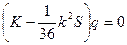 .
.
Нетривиальное решение этой системы возможно при

или

где I – единичная матрица.
Задача свелась, таким образом, к нахождению собственных значений матрицы 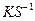 . При решении задачи на ЭВМ типа ЕС стандартная подпрограмма NROOT служит для вычисления собственных значений и собственных векторов такой матрицы.
. При решении задачи на ЭВМ типа ЕС стандартная подпрограмма NROOT служит для вычисления собственных значений и собственных векторов такой матрицы.
Минимальное собственное значение представляет собой коэффициент, соответствующий критической силе.
7.77*. Рассмотреть задачу 7.73, взяв число конечных элементов: а). n=10, б). n=16, в). n=20.Сопоставив результаты, показать, что, решая задачу на основе вариационного метода Ритца, мы получаем все более точные результаты, увеличивая число конечных элементов: при этом приближение имеет место «сверху».
Решение:
Воспользоваться ЭВМ по схеме, описанной в решении к задаче 7.76.
7.78*. Решить задачу 7.74 для стержня, шарнирно опертого по концам, принимая число конечных элементов n=6.
Решение:
По сравнению с задачей 7.76 изменятся лишь матрицы жёсткости и геометрической жёсткости граничных элементов; они будут для элемента 1-2 иметь вид по решению задачи 7.74:
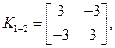

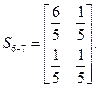
для элемента 6-7, как в задаче 7.74 для элемента 2-3:

7.79*. Рассмотреть задачу 7.74, выбрав число конечных элементов n=10.
Решение:
См. указание к задаче 7.78.
7.83*. Решить задачу 7.39 об устойчивости стержня переменного сечения при переменной по длине осевой силе, пользуясь методом конечных элементов. Разделить стержень на два конечных элемента одинаковой длины. Рассмотреть два варианта соотношения между параметрами, определяющими различные части стержня, по условию задачи 7.39.
Решение:
Основываясь на решении задачи 7.73, находим матрицы жёсткости элементов 1-2 и
2-3 с учётом различия в жесткостях этих элементов (  ):
):

 .
.
Далее сопоставляем матрицы геометрической жёсткости, принимая во внимание различие в осевых силах (  ):
):
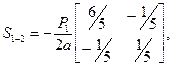
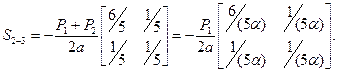
Глобальные матрицы для всего стержня находим путём сложения элементов соответствующих матриц:


Определение критического параметра по задаче 7.73 сводится к нахождению значения  , при котором определитель
, при котором определитель  равен нулю:
равен нулю:

Раскрывая определитель, получим

или
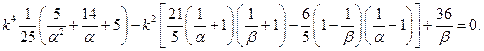 (1)
(1)
Для варианта а) при  и
и  приходим к уравнению
приходим к уравнению

тогда

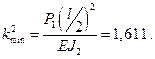
Отсюда

При указанном ответе к задаче 7.39 точном значении  погрешность составляет 2,3 %.
погрешность составляет 2,3 %.
Для варианта б) при  ,
,  уравнение (1) принимает вид
уравнение (1) принимает вид
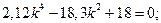
находим

Отсюда
 и
и 
Точное значение  погрешность составляет 1,46%.
погрешность составляет 1,46%.
7.84*. Стержень, заземленный по концам, подвергается действию быстро возрастающей во времени осевой нагрузки 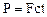 , где
, где 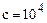 МПа/с – скорость нарастания напряжения в поперечном сечении, F - площадь сечения. Пользуясь методом конечных элементов, определить динамическую нагрузку
МПа/с – скорость нарастания напряжения в поперечном сечении, F - площадь сечения. Пользуясь методом конечных элементов, определить динамическую нагрузку  (в отношении к эйлеровой статической величине
(в отношении к эйлеровой статической величине  ), при которой имеет место катастрофический рост прогибов. Считать, что в начальный момент стержень имеет весьма малый прогиб порядка
), при которой имеет место катастрофический рост прогибов. Считать, что в начальный момент стержень имеет весьма малый прогиб порядка  м, распределенный вдоль длины по форме статической потери устойчивости. Учесть, что форма выпучивания при быстро врастающей нагрузке может существенно отличаться от случая статической нагрузки. Разделить длину стержня на шесть равных по размеру конечных элементов. Составить программу для решения задачи с помощью ЭВМ. Принять, что стержень имеет длину 1 м и круглое сечение диаметра
м, распределенный вдоль длины по форме статической потери устойчивости. Учесть, что форма выпучивания при быстро врастающей нагрузке может существенно отличаться от случая статической нагрузки. Разделить длину стержня на шесть равных по размеру конечных элементов. Составить программу для решения задачи с помощью ЭВМ. Принять, что стержень имеет длину 1 м и круглое сечение диаметра  м. Материал – сталь, плотность
м. Материал – сталь, плотность  , модуль упругости
, модуль упругости  .
.
Решение:
Кинетическая энергия конечного элемента
 (1)
(1)
Точка над булевой функцией означает дифференцирование по времени. Выразим скорость перемещений в пределах конечного элемента, как в задаче 7.73, но на этот раз относительно скоростей параметров  …,
…,  под
под 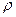 понимается плотность материала. Имеем:
понимается плотность материала. Имеем:
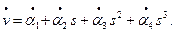
Представим 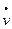 через скорости перемещения узлов
через скорости перемещения узлов 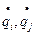 и скорости изменения углов поворота
и скорости изменения углов поворота 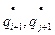 , соответствующие концам элемента
, соответствующие концам элемента  :
:



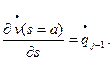
Тогда
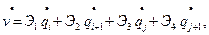
здесь Э1, …, Э4 имеют те же значения, что и в задаче 7.73. Для элемента 1-2 при 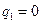 ,
, 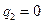


Выпишем это выражение в матричной форме:
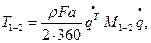
где



Для элемента 2-3 получим

Подставляя  в (1), находим
в (1), находим
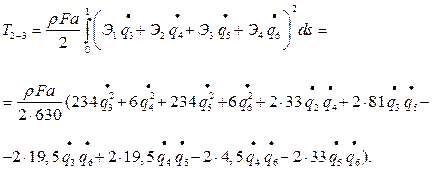
Перепишем это выражение в следующем виде:
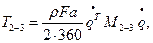
где  матрица масс:
матрица масс:
 (2)
(2)
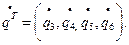
Нетрудно видеть, что матрицы масс для элементов, не примыкающих к опорам, будут такими же, что и матрица (2). Определим матрицу масс для элемента с правым защемлённым концом, когда 



или

где
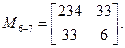
Для системы в целом

 (3)
(3)
через  здесь обозначена матрица масс для всего стержня:
здесь обозначена матрица масс для всего стержня:





при 
Выписываем уравнение Лагранжа 1)
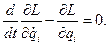
Лагранжева функция  равна
равна 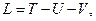
|
из
5.00
|
Обсуждение в статье: Численные методы. Применение ЭВМ. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

