Метод конечных элементов. Использование графопостроителя ЭВМ для получения эпюр.

5.148*. Для балки длины l и жёсткости EJ, защемлённой по концам и нагруженной силой посередине пролёта, определить прогиб под силой 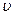/_l/2. Воспользоваться методом конечных элементов на основе вариационного принципа Ритца. Разделить балку на два конечных элемента длины a = l/2. Ввести в качестве варьируемых параметров величины прогиба и угла поворота касательной к упругой линии для узлов 1, 2, 3, расположенных по концам элементов. Сравнить результат вычислений с «точным» (в пределах теории изгиба балок) значением.

Решение:

     Исходя из принципа Ритца, выпишем условие равновесия балки в виде

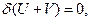                                                                                                                                                                    (1)                                            

где Э – полная потенциальная энергия системы, U – потенциальная энергия деформации, V – потенциал внешней нагрузки.

       Введём два конечных элемента длины  a = l/2 с узлами 1, 2, 3, показанными на рисунке к условию задачи. Обозначим через s = x/a безразмерную координату, отсчитываемую от левого конца каждого элемента. В качестве обобщённых координат примем q₁, q₂ – прогиб и угол поворота в узле 1, q₃, q₄ –  в узле 2, q₅, q₆ –  в узле 3.

       Примем общее выражение для прогиба в пределах конечного элемента

                                                                      ,                                            (2)

где 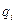,  - перемещение в угол поворота, относящееся к левому концу элемента,  и 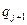 - к правому.

       В случае защемленных концов балки будет . Для первого элемента получаем прогиб равным , для второго элемента - . Здесь Э₁,…,Э₄  - так называемые эрмитовы функции

                                                                               (3)

 В решении задачи 7.73 (см. ниже) показано, что эти функции отвечают общему выражению для прогиба типа

Определим потенциальную энергию деформации элемента 1-2:

                                                                                                             (4)        

штрихи обозначают дифференцирование по s. Находим (см. также решение задачи 7.73)

                                                                                          (5)

или, в матричной форме,

                                                                                                                (6)

где 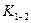 - матрица жёсткости элемента 1-2

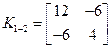                                                                                                                      (7)

q – вектор-столбец с координатами , , а  - транспонированный вектор:

                                                    

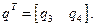
Рассматривая элемент 2-3, получим матрицу жёсткости в виде

                                                                                                                  (8)

Складывая (7) и (8), получаем общую потенциальную энергию деформации в виде

                                                                                          (9)

Вибрация U будет равна

                                                                                                                  (10)

Определим далее изменение потенциала внешней нагрузки, численно равное работе обобщённых сил Q₃, Q₄  на перемещениях q₃, q_4. По формулам (3) при s=1 =1 и =0. При статическом нагружении вариация потенциала внешних сил равна

Метод Ритца по (1) приводит, при a = l/2, к соотношению

                                                                                (11)

Так как вариации  являются произвольными, находим прогиб посередине:

                                                                                                       (12)

Это выражение совпадает с известным точным решением. Объясняется это тем, что принятое выражение для прогиба в пределах каждого из конечных элементов совпадает с истинной упругой линией. Отметим, что данная задача является в принципе статически неопределимой и что метод конечных элементов здесь соответствует известному в строительной механике методу перемещений.

 

5.149*. Рассмотреть задачу 5.148, считая балку шарнирно опёртой по концам.

Решение:

    Решение строится аналогично решению задачи 5.148. Как показано подробно в решении задачи 7.73 (см. ниже), выражение для прогиба получает в случае шарнирного опирания балки по концам вид: для первого конечного элемента 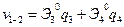, для второго , где новые эрмитовы функции

                                                                       (1)

Потенциальная энергия деформации системы оказывается (см. задачу 7.73) равной             

                                                                                                                        (2)

Матрицы жёсткости для первого и второго элементов будут

                                                                                   (3)

Полная матрица имеет вид

                                                                                                                             (4)

Изменение потенциала внешней нагрузки равно

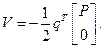
По методу Ритца, при

                                                       и                                   (5)

Это значение  совпадает с точным. И здесь легко убедиться в том, что принятая нами с помощью функций ,  упругая линия соответствует истинной.

 

5.150*. Дана балка, аналогичная рассмотренным в задачах 5.148 и 5.149, но со смешанным видом опор – шарнирной левой и защемлённой правой. Сила Р по-прежнему приложена посередине. Определить прогиб  и угол поворота  под силой.

Решение:

    Пользуемся решениями задач 5.148 и 5.149. Для левой половины балки, как в задаче 5.148

                                                                                                                     (1)

для второй половины, как в задаче 5.149,

                                                                                                                       (2)

Полная матрица жёсткости имеет вид

                                                                                                                           (3)

Обобщённая сила, соответствующая координате , равна Р; сила, соответствующая , отсутствует.

      Следовательно, приходим к уравнению

                                                                                                  (4)

При этом должны выполняться два равенства:

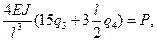                                                                                                          (5)

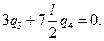                                                                                                                   (6)

Отсюда находим значения =  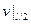и = .

 

5.151*. Рассмотреть балку с левым защемлённым концом и правым свободным. К свободному концу приложена пара сил с моментом 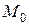. Получить эпюры моментов, углов поворота и прогибов  с помощью графопостроителя ЭВМ, принимая для примера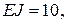

Решение:

    Повторяя выкладки задачи 5.148, получаем для прогиба выражение

                                                                                                                       (1)

Потенциальная энергия деформации равна

                                                                                                                          (2)

Матрица жёсткости

                                                                                                                        (3)

Полное уравнение

                                                                                                  (4)

Отсюда находим

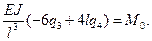                                                                               (5)

Принимая для примера значения , , 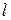, 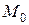указанные в условии, получаем с помощью графопостроителя ЭВМ эпюры, приведённые на рисунке.

                   

 

1) См., например, Вольмир А. С. Оболочки в потоке жидкости и газа. – М.: Наука, 1976, с. 110