 |
Главная |
Свойства определителей
|
из
5.00
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Г.В. ПЛЕХАНОВА
ИВАНОВСКИЙ ФИЛИАЛ
Кафедра Математики, экономической информатики
и вычислительной техники
ЛИНЕЙНАЯ АЛГЕБРА
Методические указания
для самостоятельной работы
студентов 1 курса заочной форм обучения
2014
Составители В.А.Тимохина, Н.Н. Груздева
Методические указания по дисциплине «Линейная алгебра» содержат конспект лекций, решенные задачи для студентов заочной формы обучения.
Содержание
1. ЛИНЕЙНАЯ АЛГЕБРА.. 4
1.1. Определители и их свойства. 4
1.1.1. Свойства определителей. 5
1.2. Матрица. Свойства и действия над матрицами. 6
1.2.1. Свойства матриц. 7
1.2.2. Действия над матрицами. 7
1.3. Решение системы линейных уравнений. 9
1.3.1 Метод Крамера. 9
1.3.2.Метод Гаусса. 10
1.3.3. Матричный метод. 12
2. ВЕКТОРНАЯ АЛГЕБРА.. 13
2.1. Векторы. Действия над векторами. 13
2.2. Линейная независимость векторов. 14
3. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.. 16
3.1. Уравнение прямой в пространстве. 16
3.2. Уравнение плоскости. 17
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.. 19
1. ЛИНЕЙНАЯ АЛГЕБРА
Определители и их свойства
Определение. Определителем второго порядка называется число, записанное в виде

Первый индекс указывает на номер строки, второй – номер столбца.
Определителем n -го порядка называется число

Число aij называется элементом определителя; i- указывает номер строки, j- номер столбца.
Для изучения свойств определителя будем рассматривать определитель третьего порядка.
Это есть число 
Определитель третьего порядка можно вычислить двумя способами:
1) правило треугольников

2) метод понижения порядка (ф-ла разложения определителя 3-го порядка по элементам 1-ой строки)
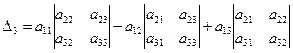
Минором Мi j данного элемента определителя третьего порядка называется определитель второго порядка, полученный путем вычеркивания i-ой строки j-го столбца.
Алгебраическим дополнением Аij данного элемента, называется его минор, умноженный на  , где к-сумма номеров строки и столбца, содержащих данный элемент:
, где к-сумма номеров строки и столбца, содержащих данный элемент:  .
.
Таким образом, знак который при этом присваивается минору соответствующего элемента определителя определяется следующей
таблицей,  т.е. знаки чередуются.
т.е. знаки чередуются.
Число миноров k-го порядка для матрицы Аmxn определяется по формуле 
Например, для определителя 3-го порядка число миноров равно 
Свойства определителей
1. Определитель не изменится, если строки определителя заменить столбцами, а столбцы, соответствующими строками.
2. Общий множитель элементов какой-нибудь строки (столбца) может быть вынесен за знак определителя.

3. Определитель меняет знак, если две строки или столбца поменять местами.
4. Определитель, содержащий две одинаковые строки или два одинаковых столбца равен нулю. (Определитель равен 0, если элементы каких- либо 2-х строк (столбцов) пропорциональны)
5. Определитель не изменится, если к элементам одной строки (столбца) определителя прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число.

ПРИМЕР 1. Вычислить определитель 
1. Правило треугольников


2. Метод понижения порядка

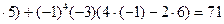
|
из
5.00
|
Обсуждение в статье: Свойства определителей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

