 |
Главная |
Классы эквивалентности
|
из
5.00
|
Пусть ε – отношение эквивалентности на множестве А. а 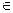 А.
А.
Опр. Классом эквивалентности, образованным элементом а называется множество элементов х 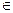 А, таких что х ~ а. Обозначается класс эквивалентности через
А, таких что х ~ а. Обозначается класс эквивалентности через  .
.
Если отношение ε – эквивалентность на множестве Z, заданная следующим образом: а ε b ↔ а и b имеют одинаковые остатки при делении на 3, то 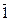 = {х
= {х 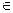 Z / х ~ 1}. Легко видеть, что числа эквивалентные единице, это все числа, которые при делении на 3 дают остаток 1, поэтому можно записать следующее:
Z / х ~ 1}. Легко видеть, что числа эквивалентные единице, это все числа, которые при делении на 3 дают остаток 1, поэтому можно записать следующее:
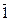 = {х
= {х 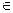 Z / х = 3к + 1, к
Z / х = 3к + 1, к 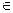 Z}. Аналогично,
Z}. Аналогично, 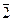 = { х
= { х 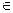 Z / х = 3к + 2, к
Z / х = 3к + 2, к 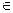 Z}и т. д.
Z}и т. д.
Классы эквивалентности обладают следующими свойствами:
1. Каждый класс эквивалентности не пустой.
В силу свойства рефлексивности а 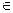
 .
.
2. Если b 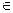
 , то
, то 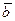 =
=  , т. е. класс эквивалентности однозначно определяется любым своим элементом.
, т. е. класс эквивалентности однозначно определяется любым своим элементом.
Пусть b 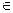
 , т. е. b ~ а. Для доказательства
, т. е. b ~ а. Для доказательства 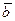 =
=  воспользуемся определением равных множеств, т. е.
воспользуемся определением равных множеств, т. е. 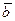 =
=  тогда и только тогда, когда
тогда и только тогда, когда 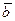
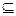
 и
и 
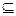
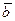 .
.
Покажем, что 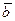
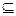
 . Пусть u
. Пусть u 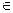
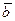 , тогда u ~ b и по условию b ~ а. По свойству транзитивности имеем, что u ~ а. Следовательно, u
, тогда u ~ b и по условию b ~ а. По свойству транзитивности имеем, что u ~ а. Следовательно, u 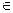
 . По определения включения
. По определения включения 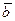
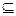
 . Аналогично доказывается, что
. Аналогично доказывается, что 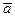
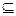
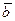 . Т. о.
. Т. о. 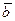 =
=  . Свойство доказано.
. Свойство доказано.
3. Классы эквивалентности совпадают или не пересекаются.
Доказательство. Пусть имеются классы эквивалентности  ,
, 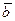 . Если
. Если 
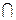
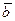 = Ø, то свойство верно. Предположим, что
= Ø, то свойство верно. Предположим, что 
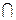
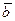 ≠ Ø. Т. е. существует элемент с
≠ Ø. Т. е. существует элемент с 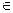

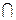
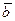 . По определению пересечения, с
. По определению пересечения, с 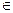
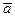 и с
и с 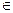
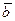 . Из предыдущего свойства следует, что т. к. с
. Из предыдущего свойства следует, что т. к. с 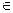
 , то
, то 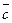 =
=  и т. к. с
и т. к. с 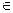
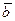 , то
, то 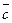 =
= 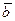 .Получаем. что
.Получаем. что 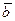 =
= 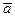 , т. е. классы эквивалентности совпали. Свойство доказано.
, т. е. классы эквивалентности совпали. Свойство доказано.
4. Объединение классов эквивалентности составляет множество А, т. е. 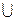
 = А.
= А.
Для доказательства достаточно воспользоваться определением равенства двух множеств. 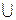
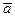 = А тогда и только тогда, когда
= А тогда и только тогда, когда 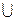

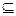 А и А
А и А 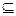
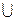
 , т. е. показать, что любой элемент х
, т. е. показать, что любой элемент х 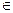
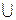
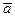 будет принадлежать множеству А и наоборот.
будет принадлежать множеству А и наоборот.
Разбиение множества
Множество всех различных классов эквивалентности множества А по эквивалентности ε обозначается через А/ ε и называется фактор – множеством множества А по эквивалентности ε.
По сути, отношение эквивалентности является обобщением понятия равенства. Некоторый общий способ задания отношений эквивалентности на произвольном множестве А связан с понятием разбиения множества.
Опр. Система непустых подмножеств множества А называется разбиением множества А, если выполнены условия:
1. Подмножества не пересекаются;
2. Объединение подмножеств составляет множество А.
Разбиение множества обозначается символом S(А).
Пример. А = Z
Разбиение множества Z составляют такие подмножества целых чисел: А1 = {0}, А2 = {Z+}, А3 = {Z-}. Имеет место запись S(Z) = {А1, А2, А3}
Связь между эквивалентностью и разбиением выражена следующей теоремой:
Теорема. Любое отношение эквивалентности на множестве вызывает разбиение этого множества . Любое разбиение множества задает на этом множестве отношение эквивалентности.
Доказательство. Покажем, что отношение эквивалентности ε на множестве А вызывает разбиение этого множества S(А) . Т. к. на множестве А задана эквивалентность ε, то можно рассмотреть классы эквивалентности  . Выберем все различные классы эквивалентности и составим из них множество – фактор множество множества А по эквивалентности ε - А/ ε. Сравним S(А) и А/ ε. Они оба состоят из подмножеств множества А и обладают одинаковыми свойствами. Т. е. S(А) = А/ ε. Т.о. фактор множества множества А по эквивалентности ε задает разбиение этого множества.
. Выберем все различные классы эквивалентности и составим из них множество – фактор множество множества А по эквивалентности ε - А/ ε. Сравним S(А) и А/ ε. Они оба состоят из подмножеств множества А и обладают одинаковыми свойствами. Т. е. S(А) = А/ ε. Т.о. фактор множества множества А по эквивалентности ε задает разбиение этого множества.
Покажем , что разбиение множества S(А) задает на этом множестве А отношение эквивалентности. Зададим бинарное отношение ρ по следующему правилу: для любых элементов а, b 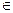 А (а ρ b ↔ а и b принадлежат одному классу разбиения). Докажем, что ρ – эквивалентность. Для этого проверим следующие свойства:
А (а ρ b ↔ а и b принадлежат одному классу разбиения). Докажем, что ρ – эквивалентность. Для этого проверим следующие свойства:
1. рефлексивность
Свойство рефлексивности выполняется, т. к. для любого элемента а 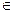 А найдется класс разбиения. Если бы такой класс не нашелся, то объединение классов разбиения не равнялось бы множеству А.
А найдется класс разбиения. Если бы такой класс не нашелся, то объединение классов разбиения не равнялось бы множеству А.
2. симметричность
Свойство симметричности выполняется, т. к. для любых двух элементов а, b 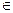 А из того что а, b принадлежат классу разбиения Ах следует, что и b, а
А из того что а, b принадлежат классу разбиения Ах следует, что и b, а 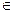 Ах.
Ах.
3. транзитивность
Возьмем произвольные элементы а, b, с 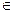 А, такие что а, b
А, такие что а, b 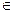 Ах и b, с
Ах и b, с 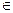 Ау. Классы разбиения не пересекаются, т. е. Ах
Ау. Классы разбиения не пересекаются, т. е. Ах 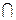 Ау = Ø. Следовательно Ах = Ау. А это значит, что а, в, с принадлежат одному классу разбиения. Свойство транзитивности выполняется.
Ау = Ø. Следовательно Ах = Ау. А это значит, что а, в, с принадлежат одному классу разбиения. Свойство транзитивности выполняется.
Т. к. все три свойства выполняются, то ρ является отношением эквивалентности.
Терема доказана.
Отношение порядка
Опр. Отношение ρ на множестве А называется отношением порядка на множестве А, если оно транзитивно и антисимметрично.
Пример. Отношение ≥ на множестве Z является отношением порядка.
Опр. Отношение порядка ρ на множестве А называется отношением нестрогого порядка на множестве А, если оно рефлексивно.
Пример. Отношение делимости на множестве N является отношением нестрогого порядка.
Опр. Отношение порядка ρ на множестве А называется отношением строгого порядка, если оно антирефлексивно.
Пример. Отношение > на множестве R является отношением строгого порядка.
Опр. Отношение порядка ρ на множестве А называется отношением линейного порядка, если для любых х, у 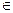 А либо х = у, либо х ρ у, либо у ρ х.
А либо х = у, либо х ρ у, либо у ρ х.
Пример. Отношение < на множестве Z является отношением линейного порядка.
Отношение порядка, не являющегося линейным, называется частичным порядком.
Пример. Пусть Р(N) множество всех подмножеств множества N. Отношение включения на множестве Р(N) – отношение частичного порядка.
Опр. Множество А на котором введено отношение порядка ρ называется упорядоченным. Если порядок линейный, то пара (А, ρ) называется линейно упорядоченным множеством. Если порядок частичный, то пара (А, ρ) называется частично упорядоченным множеством.
|
из
5.00
|
Обсуждение в статье: Классы эквивалентности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

