Представление бинарных отношений графами

Раздел 2. Алгебра отношений

Прямое произведение

Пусть А ≠ Ø, В ≠ Ø

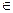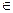Опр. Прямым произведением двух множеств А и В называется множество элементов А×В, состоящее из всех пар (а, b), где а  А, b  В.

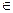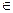А×В = {(а, b) / а  А, b  В}

Пример. Если А = {а₁, а₂}, В = {b₁, b₂, b₃}, то А×В = {(а₁, b₁), (a₁, b₂), (a₁, b₃), (a₂, b₁), (a₂, b₂), (a₂,b₃)}.

Если А = [0, 3], В = [0, 2], то множество А×В изобразится заштрихованной частью координатной плоскости (рис. )

Аналогично можно рассмотреть прямое произведение трех,…, n множеств.

А₁×А₂×…×А_n = {(а₁, а₂, …, а_n) / а₁ 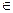А₁, а₂ 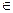А₂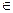, …, а_n А_n}

Из определения следует, что прямое произведение множеств А, В не коммутативно, т.е. А×В ≠ В×А.

Пусть а, b – какие – нибудь объекты. Если а = b, то множество {а,b} есть неупорядоченная пара элементов и {a, b}={b, a}.

Введем новое понятие – упорядоченная пара. Любым двум объектам а и b поставим в соответствие новый объект – их упорядоченную пару (а, b), где а – первая компонента, b – вторая компонента. Очевидно, что пара (а, b) = (с, d) тогда и только тогда, когда а = с и b = d. Исходя из понятия упорядоченной пары можно дать другое определение прямого произведения.

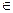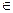Опр. Прямым произведением множеств А и В называется множество А×В, состоящее из всех упорядоченных пар (а, b), где а  А, b  В.

Если А = В, тогда А×В = А×А = А² – прямой квадрат.

Бинарные отношения

Одним из основных понятий в теории множеств является понятие бинарного отношения.

Опр. Любое подмножество ρ прямого произведения А×В, где А, В – произвольные множества, называется бинарным отношением между множествами А и В.

Из определения следует, что:

1. элементами бинарного отношения являются пары принадлежащие прямому произведению А×В;

2. поскольку ρ множество, то его можно задать также как множества, т.е. перечислением пар отношения или заданием свойства элементов ρ;

Пример 1. ρ₁ 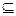R×Z, ρ₁ = {(0,5;1), (3, -8), (0,0)}

Пример 2. ρ₂ 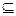R×R, ρ₂ = {(x, y) / y = sin x} = {(0,0), ( , 1), ( , 0), …}

3. бинарных отношений между А и В будет столько, сколько подмножеств у прямого произведения А×В.

Если пара (а, b) 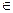 ρ, то говорят, что элемент а находится в отношении ρ к элементу b. Вместо записи (а, b)  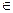ρ коротко пишут а ρ b.

Множества А×В, Ø являются подмножествами прямого произведения А×В, их соответственно называют полным и пустым отношением.

Опр. Множество первых компонент всех пар бинарного отношения ρ называется областью определения этого отношения и обозначается Dom ρ.

Dom ρ = {а 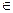А /  b 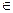В, а ρ b }

Опр. Множество вторых компонент всех пар бинарного отношения ρ называется областью значения этого отношения и обозначается Im ρ.

Im ρ = {b 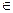В /  а 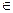А, а ρ b}

Пример. Ρ = {(0,1), (9, -2), (6, 8)}

Dom ρ = {0, 9, 6}

Im ρ = {1, -2, 8}

Аналогично можно рассматривать n – арные отношения, т.е. отношения ранга n.

ρ 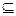 А₁×А₂×…×А_n.

Наибольший интерес представляют отношения заданные на одном множестве. Если А = В, то ρ 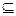А×А = А² называется отношением на множестве А.

Пример. Отношение > на множестве R: ρ = {(х, у) /  х > у}. График данного бинарного отношения выглядит следующим образом (рис. )

Бинарные отношения называются равными, если они равны как множества.

Опр. Пусть ρ, φ – бинарные отношения. Множества пар (х, у) таких, что для некоторого z пара (х, z) 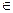 φ и пара (z, у)  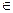ρ, называется композицией (суперпозицией) отношений φ, ρ, и обозначается ρ · φ.

ρ · φ = {(х,у) / z (x φ z  и z ρ у)}

Пример. ρ = {(1, 2), (3, 4), (-1, 2)}

φ = {(2, 1), (4, 5), (2, 4)}

   φ · ρ = {(1, 1), (1, 4), (3,5), (-1,1), (-1,4)}

Композиция бинарных отношений ассоциативна, т. е. (ψ · φ) · ρ = ψ ·( φ · ρ).

Опр. Инверсией  бинарного отношения ρ называется множество всех упорядоченных пар (а, b) таких, что если пара (а, b) 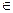 ρ, то пара (b, а) .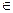

Пример. ρ = {(1, 6), (2, 7), (2, 2)}

 = {(6, 1), (7,2), (2,2)}

Опр. Пусть ρ – бинарное отношение на множестве А. Степенью отношения ρ на множестве А называется его композиция с самим собой. Обозначается ρⁿ = ρ·ρ·…·ρ

ρ⁰ = 1, ρ¹ = ρ, ρ² = ρ·ρ, …, ρⁿ = ρ^n-1· ρ.

Теорема. Если некоторая пара (а, b) принадлежит какой – либо степени отношения ρ на множестве А мощности n , то эта пара принадлежит и степени ρ не выше n – 1.

Представление бинарных отношений графами

Опр. Графом называется фигура на плоскости, состоящая из конечного числа точек – вершин графа, и линий, соединяющих некоторые из вершин. Линия, соединяющая какие – либо две вершины графа, называется ребром графа. Точки пересечения ребер могут не являться вершинами графа. Граф, на котором стрелками указаны направления всех ребер, называется ориентированным. 

Существует простой способ представления бинарных отношений на конечных множествах графами. Пусть А ≠ Ø, ρ 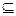А×А. Элементы множества А изобразим на плоскости точками. Каждой паре (а, b) 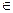ρ поставим в соответствие ориентированное ребро (рис. ), идущее от точки а к точке b. Паре (а, а) ставим в соответствие петлю (рис. ) с фиксированным направлением обхода.

Пример. На рис. Изображен граф отношения

φ = {(1, 2), (3, 4), (4, 1), (5, 5)}

Ребро с двумя стрелками называется неориентированным.

Каждое бинарное отношение на конечном множестве можно представить ориентированным графом. С другой стороны, каждый ориентированный граф представляет бинарное отношение на множестве его вершин.