 |
Главная |
Пример из демоверсии ЕГЭ 2018 (профильный уровень)
|
из
5.00
|
Задание 19.
Что можно ожидать в качестве задания 19 на экзамене?
| Тип задания | Уметь строить и исследовать простейшие математические модели | |
| Характеристика задания | Задача, связанная со свойством делимости целых чисел, логическим перебором. | |
| Описание | Задание олимпиадного типа, рассчитанное на сильных учеников. Для того чтобы продвинуться в решении не требуется никаких специальных знаний, выходящих за рамки стандарта математического образования. Однако, необходимо проявить определенный уровень математической культуры, логического мышления, который формируется на протяжении всего обучения в школе. Ответ на первый вопрос по силам большинству успевающих учеников. Главное здесь – не испугаться условия, дочитать до конца и подумать.
| |
Общность всех формулировок заданий №19
С 2010 года вариант ЕГЭ по математике содержит четырехбалльное задание С6 (в этом году №19) олимпиадного характера. Большую долю среди задач, уже использованных в вариантах экзамена, составляют задачи на последовательности
(чисел, ходов, наборов чисел и т.д.). Характерной особенностью подобных задач является исследование элементов заданной последовательности следующего вида:
а) на наличие элемента, обладающего заданным свойством;
б) подсчет количества элементов, обладающих заданным свойством;
в) оценка (наибольшего или наименьшего значения) либо количества элементов, обладающих заданным свойством, либо некоторой числовой характеристики заданных элементов;
г) приведение примера, подтверждающего полученную оценку (подразумевается, но в условии не формулируется!).
Критерии оценивания задания №19 (первичный балл)
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. крит. на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. крит. на 1 балл) результатов | 2 |
| Верно получен один из следующих результатов: – пример в п. а; – обоснованное решение п. б; – искомая оценка в п. в; – пример в п. в, обеспечивающий точность предыдущей оценки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
Основные олимпиадные идеи, используемые при решении подобных задач
1. Идея «чет-нечет». Используется, когда рассматриваемая величина (например, сумма или произведение) имеет определённую чётность, что позволяет доказать невозможность ситуации, в которых она имеет другую чётность.
2. Уравнения в целых числах. Используемые в решении формулы (например, общего члена прогрессии, суммы n первых членов прогрессии, характеристическое свойство) в силу целочисленности входящих в них переменных приводят к необходимости исследования уравнения в целых числах.
3. Свойства делимости целых чисел (признаки делимости, деление без остатка, деление с остатком, анализ остатков).
4. Идея «усиления неравенства», используемая при замене в неравенстве какой-нибудь переменной на ее возможное наибольшее или наименьшее значение.
5. Метод «перебора» значений целочисленной переменной из ограниченного набора.
Классификация заданий 19 ЕГЭ, в которых присутствуют последовательности
1. Задачи на арифметическую прогрессию.
2. Задачи на геометрическую прогрессию.
3. Задачи на произвольные последовательности чисел, заданные формулой n-го члена или каким-либо ограничением, накладываемым на их элементы.
4. Задачи на последовательности наборов чисел.
5. Задачи на последовательности ходов.
Как правило, во всех подобных задачах оговаривается целочисленность элементов членов последовательностей, элементов в наборах чисел или элементов, получаемых на каждом шаге в последовательности ходов.
Пример из демоверсии ЕГЭ 2018 (профильный уровень)

Решение:


ОТВЕТ: а) 44; б) отрицательных; в) 17.
Основная теорема арифметики. Для каждого натурального числа, большего единицы, существует единственное разложение на простые множители.
Каноническое разложение целого числа n>1:
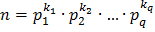 где
где 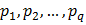 – попарно различные простые числа, а – попарно различные простые числа, а 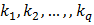 – натуральные числа. – натуральные числа.
|
Признаки делимости целых чисел:
На 3 и на 9: Натуральное число делится на 3(9) тогда и только тогда, когда сумма цифр этого числа делится на 3(9).
На 5. Натуральное число делится на 5 тогда и только тогда, когда последняя цифра этого числа равна 5 или 0.
На 7. Натуральное число делится на 7, если разность — это число без его последней цифры минус удвоенная последняя цифра — делится на 7.
На 11. Число делится на 11, если знакочередующаяся сумма его цифр делится на 11. Термин «знакочередующаяся» означает, что первое слагаемое суммы берётся со знаком «плюс», второе — со знаком «минус», третье — опять со знаком «плюс» и т.д. То есть знаки перед слагаемыми чередуются.
Задачи на делимость
Пример 1. Сборник ЕГЭ-2017 12.6)(делимость чисел) Пусть p >3–простое число. Доказать, что p 2 -1 делится на 24.
Решение.
Делимость на 24 обеспечивается одновременной делимостью числа на 3 и на 8. (Следует из единственности разложения на простые множители).
p 2 -1 = (p -1)(p +1), p – нечетное (иначе оно в условиях задачи не простое), следовательно p -1, p +1 – четные. Пусть p -1 = 2k, тогда p +1 =2(k+1).
(p -1)(p +1)=4k(k+1), при этом либо k либо k+1 – четные. Поэтому (p -1)( p +1) делиться на 8.
Осталось показать, что (p -1)( p +1) делиться на 3. Очевидно, что p не кратно 3. Тогда остаток от деления p на 3 равен либо 1, либо 2.
Пусть p=3k+1, тогда (p-1)( p+1)= 3k(3k+2) – кратно 3.
Пусть p=3k+2, тогда (p-1)( p+1)= (3k+2)(3k+3) (3k+2)3(k+1) – кратно 3.
Следовательно, p2-1 всегда делится на 3 и на 8, то есть делиться на 24.
Пример 2. Найти все натуральные числа вида 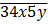 , которые делятся на 36.
, которые делятся на 36.
Решение:
В соответствии с основной теоремой арифметики для того, чтобы число делилось на 36 необходимо, чтобы в его разложении на простые множители присутствовали множители 22k и 32q, где k,q – натуральнее числа.
Иными словами, число должно делиться на 4 и на 9 одновременно.
Следовательно, сумма цифр должна делиться на 9.
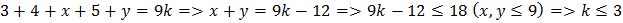
Понятно, что k>1 (иначе 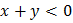 ).
).
Получаем два варианта: k=2 или 3. То есть 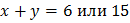 .
.
Представим 6 в виде суммы 6=1+5=0+6=2+4=3+3. Пары (1,5) и (3,3) не удовлетворяют условию, т.к. получится нечетное число. Следовательно, получим 4 возможных варианта 34056, 34650,34254,34452. Из них делятся на 4 только 34056 и 34452.
Представим 15 в виде суммы цифр: 15=7+8=9+6. Оканчиваться число может только на четную цифру. Т.о. еще два кандидата : 34758 и 34956. Последние число удовлетворяет условию задачи.
Ответ: 34056, 34452,34956
Пример 3. (Пробный вариант ЕГЭ 2018) Может ли произведение цифр натурального числа быть:
а) Больше 126 и меньше 130;
б) Больше 731 и меньше 736;
в) Больше 887 и меньше 894.
Если такие числа существуют, то в пункте а) необходимо указать хотя бы одно значение, в б) и в) – все значения.
Основная идея в решении, позволяющая сократить перебор вариантов – использование основной теоремы арифметики (единственность разложения любого натурального числа на простые множители).
Для проверки числа на простоту (в задании такие встречаются) используем критерий простого числа: если число A не делится ни на один простой множитель, не превышающий 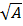 , то A – простое.
, то A – простое.
Произведение цифр натурального числа –натуральное число, причёт оно обязано раскладываться на простые множители, каждый из которых не превышает 9 (т.к. цифр всего 9). Следовательно, если в разложении на простые множители какого-либо числа присутствуют простые, отличные от 2,3, 5, 7, то это число не может быть произведением цифр натурального числа.
а) 127 – простое (не делится на 2,3,5,7,11 < 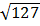 ). Не может быть произведением цифр натурального числа.
). Не может быть произведением цифр натурального числа.
128=26. Удовлетворяет условию, например число 222222 или 444
129=3·43 – не удовлетворяет условию.
б) 732 = 61·3·22 – не удовлетворяет условию;
733 – простое число, не удовлетворяет условию;
734 = 2·367 - не удовлетворяет условию;
735=5·3·72 - удовлетворяет условию числа 3577, 5377, 7753, 7735, 7537, 7357, 3757, 5737,7375, 7573,3775,5773;
Таким образом, ни одно из чисел пункта б) не может быть произведением цифр натурального числа.
в) 888,889,890,891,892,893
888=23·3·37 – не удовлетворяет условию;
889 =127·7 – не удовлетворяет условию;
890=5·2·89 – не удовлетворяет условию;
891=34·11 – не удовлетворяет условию;
892=22·223 – не удовлетворяет условию;
893=19·47 – не удовлетворяет условию;
Таким образом, ни одно из чисел пункта б) не может быть произведением цифр натурального числа.
Ответ: а) да 128 (444 или 222222 или 284…), б) да -735 (3577, 5377, 7753, 7735, 7537, 7357, 3757, 5737,7375, 7573,3775,5773); в) нет
Задачи на арифметическую и геометрическую прогрессии
Набор основных формул для арифметической прогрессии.

Полезные факты о геометрической прогрессии:

Пример 4. (арифметическая прогрессия)
Дано n различных натуральных чисел (не менее трех), составляющих арифметическую прогрессию.
а) Может ли сумма всех данных чисел быть равной 18?
б) Каково наибольшее значение n, если сумма всех данных чисел меньше 800?
в) Найдите все возможные значения n, если сумма всех данных чисел равна 111.
Решение:
а) Здесь работает метод направленного перебора. Заметим, что либо два из трёх чисел обязательно нечетны, а одно – четно, либо все три - четные (иначе сумма трех чисел не будет четной). Подходит, например, тройка 5,6,7.
Вот здесь можно применить врезку из видео – идея чет и нечет
https://www.youtube.com/watch?v=2NkvkX9LGFM&list=PLFBCHVQg5AWX7qT5jrP2AbC1Yvn_eQThh
б) Работает подход – оценка + пример. Пусть наша прогрессия будет возрастающая 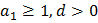 . Сначала оценим количество элементов прогрессии через оценку суммы прогрессии (усиление неравенства):
. Сначала оценим количество элементов прогрессии через оценку суммы прогрессии (усиление неравенства):
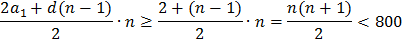
Следовательно: n≤39. Для отрезка натурального ряда : 1, 2,…,39 сумма равна 780. Следовательно наибольшее количество чисел – 39
в) В этой задаче, как и в большинстве задач на целые числа, необходимо разложить заданную сумму на простые множители 111= 37·3.
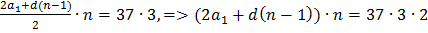
Если n≥37, то 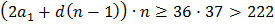 . То есть n<37
. То есть n<37
Осталось разобрать случаи n=3, 6. Примеры таких прогрессий: 36,37,38; 16,17,18,19,20,21.
ОТВЕТ: а) 5,67; б) 39; в) 3 и 6.
Пример 5. (геометрическая прогрессия)
Все члены геометрической прогрессии – различные натуральные числа, заключенные между числами 210 и 350. а) Может ли такая прогрессия состоять из четырех членов? б) Может ли такая прогрессия состоять из пяти членов?

что противоречит условию задачи. ОТВЕТ: а) да; б) НЕТ.
Задачи для самостоятельного решения:
1. Несколько различных натуральных чисел, в десятичной записи которых отсутствуют цифры 1 и 9, составляют арифметическую прогрессию.
а) Может ли сумма всех членов такой прогрессии быть равной 298?
б) Может ли в прогрессии быть 35 членов?
в) Показать, что если разность этой прогрессии не меньше 4, но не больше 8, то количество членов не превосходит 18.
г) Привести пример, когда разность арифметической прогрессии не меньше 4, но не больше 8, а количество членов равно 18.
2. (Досрочный ЕГЭ -2018) На доске написаны числа 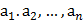 каждое из которых не меньше 50 но не больше 150. Каждое из чисел
каждое из которых не меньше 50 но не больше 150. Каждое из чисел 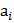 уменьшили на ri%. При этом для каждого i (1≤ i ≤ n ) либо ri равно 2, либо число
уменьшили на ri%. При этом для каждого i (1≤ i ≤ n ) либо ri равно 2, либо число 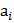 уменьшилось на 2.
уменьшилось на 2.
а) Может ли оказаться, что среднее арифметическое чисел 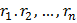 равно 5?
равно 5?
б) Может ли оказаться, что среднее арифметическое чисел 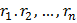 больше 2, а сумма чисел
больше 2, а сумма чисел 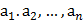 уменьшилась более, чем на 2n?
уменьшилась более, чем на 2n?
в) Пусть на доске написано 30 чисел, сумма которых уменьшилась на 40. Найдите наибольшее значение среднего арифметического  .
.
Здесь нужно дать краткий обзор понятия сравнения чисел по модулю и привести пример таблиц умножения/сложения остатков от деления. (подробно в прилагаемом фале Арифметика остатков.pdf)
Задачи на последовательности
Иногда последовательность чисел задается возвратным уравнением 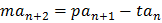 .
.
Рассмотрим один частный случай, используемый в подобных задачах.
Пусть последовательность задана уравнением 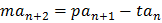 , где p = m + t . Тогда
, где p = m + t . Тогда 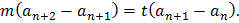 Обозначив
Обозначив 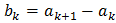 , получаем
, получаем 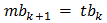 , то есть
, то есть 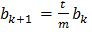 .
.
Значит, 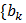 } – геометрическая прогрессия со знаменателем q=
} – геометрическая прогрессия со знаменателем q=  .
.
Так как 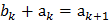 ,
,
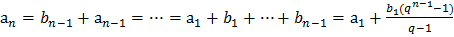
Пример 6. Конечная возрастающая последовательность 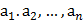 состоит из n ≥3 различных натуральных чисел, причем при всех натуральных k ≤ n -2 выполнено равенство
состоит из n ≥3 различных натуральных чисел, причем при всех натуральных k ≤ n -2 выполнено равенство 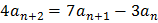
а) Приведите пример такой последовательности при n =5.
б) Может ли в такой последовательности при некотором n ≥3 выполняться равенство 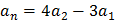 ?
?
в) Какое наименьшее значение может принимать 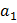 если
если 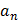 =527?
=527?
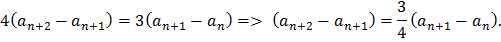
Обозначим 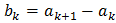 , тогда
, тогда 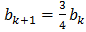 .
.
a) 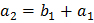 ,
, 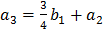 ,
, 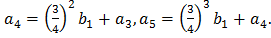
Пусть 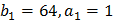 , тогда получим последовательность : 1, 65, 113,149,176.
, тогда получим последовательность : 1, 65, 113,149,176.
б) Нет, не может, так как q= 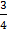 и
и 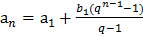 , следовательно (усилим неравенство):
, следовательно (усилим неравенство): 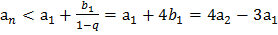 .
.
в) 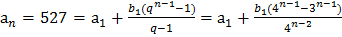
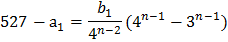
для нескольких n ≥3 выпишем 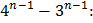
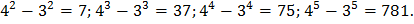
Для того, чтобы 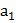 было целым числом необходимо, чтобы
было целым числом необходимо, чтобы 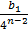 было целым. Это можно обеспечить выбором
было целым. Это можно обеспечить выбором 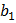 . Поэтому разность
. Поэтому разность 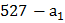 должна быть кратна
должна быть кратна 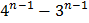 .
.
Рассмотрим остатки от деления 527 на 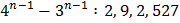 . Минимальный остаток 2. Тогда при
. Минимальный остаток 2. Тогда при 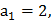 левая часть делиться на
левая часть делиться на 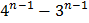 нацело при n =3;5.
нацело при n =3;5.
(Здесь работает теорема о сложении остатков или сложении по модулю – смотри файл Арифметика остатков.)
Следовательно, наименьшее удовлетворяющее условию задачи значение – 2.
Пример последовательности 2, 302,527.
ОТВЕТ: а) например, 1, 65, 113, 149, 176; б) нет; в) 2.
Пример 7. ( ЕГЭ 2016) В конечной последовательности 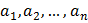 , состоящей из целых чисел,
, состоящей из целых чисел, 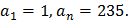 Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности;
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа элементов может состоять такая последовательность?
Решение. а) 1, 4, 21, –16, 41, –36, 61, –56, 81, – 78, 103, –100, 125, –122, 147, –144, 169, –166, 191, –188, 213, –210, 235.
б) Нет. Поскольку сумма двух соседних членов есть нечетное число, они имеют разную четность. Следовательно, все члены с нечетными индексами нечетны, а с четными - четны. Поэтому 1000-й член не может равняться 235.
в) Рассмотрим три последовательных члена последовательности
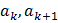 ,
, 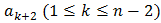
Поскольку 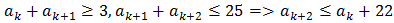
Последовательность состоит из нечетного числа членов.
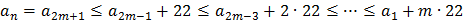
Следовательно: 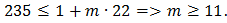
Значит, последовательность состоит из не менее 23 членов. Пример пункта а) удовлетворяет этой оценке.
Ответ: б) нет; в) 23.
|
из
5.00
|
Обсуждение в статье: Пример из демоверсии ЕГЭ 2018 (профильный уровень) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

