 |
Главная |
Свойства области сходимости
|
из
5.00
|
Z преобразование
И так, перейдем к Z-преобразованию, которое аналогично преобразованию Лапласа для непрерывных сигналов. Эти преобразования имеют схожую связь с преобразованием Фурье.
Для чего это нужно? Во первых, Фурье преобразование определено далеко не для всех последовательностей, Z-преобразование применимо для более широкого класса сигналов. Во вторых, аналитическая запись Z-преобразования более удобная, чем преобразования Фурье.
Как мы проходили ранее, преобразование Фурье дискретного сигнала (последовательности) имеет вид
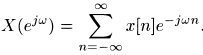
Заменим 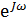 на Z. Тогда получим
на Z. Тогда получим
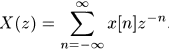
Такой степенной ряд называется рядом Лорана и очень подробно изучается в ТФКП
Такая подстановка ( 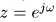 ) означает ограничение переменной z в Z преобразовании на единичную окружность.
) означает ограничение переменной z в Z преобразовании на единичную окружность.
Z преобразование, как функцию комплексной переменной, удобно описывать с помощью комплексной плоскости. Геометрическое место точек |z| = 1 на ней (плоскости), удовлетворяющих условию |z| = 1, представляет собой окружность единичного радиуса с центром в нуле.
Z-преобразование, вычисляемое только на единичной окружности, совпадает с преобразованием Фурье.
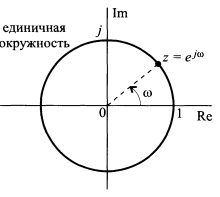
| 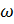 – угол между радиус вектором и действительной осью. При вычислении Х(z) в точках единичной окружности, начиная с z=1 ( – угол между радиус вектором и действительной осью. При вычислении Х(z) в точках единичной окружности, начиная с z=1 ( 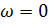 ) и далее, в направлении z=-1 ( ) и далее, в направлении z=-1 ( 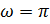 ) через z=j ( ) через z=j ( 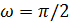 ) мы получаем Фурье образ на промежутке ( ) мы получаем Фурье образ на промежутке ( 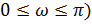 . Продолжая, мы найдем значение Фурье-образа на всем периоде. . Продолжая, мы найдем значение Фурье-образа на всем периоде.
|
При Фурье преобразовании мы имеем функцию от вещественной переменной, изменяющейся вдоль частотной прямой.
Интерпретация Фурье преобразования, как ограничения переменной z единичной окружностью, концептуально означает, что мы частотную ось обернули на единичную окружность. При этом, периодичность получается сама собой, как изменение угла на 2 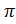 радиан.
радиан.
Область сходимости
И так, как мы знаем, степенной ряд Фурье сходится далеко не для всех последовательностей (т.е. значение бесконечной суммы может не быть конечным). Так же и для Z преобразований – оно сходится не для всех последовательностей.
Множество тех значений z, при которых степенной ряд сходится, называют областью сходимости.
Например, последовательность единичного скачка u[n] не сходится, следовательно, ее Фурье образ не сходится. Однако, u[n]z-n сходится при значениях z>1, Это означает, что Z преобразование единичного скачка существует, а его область сходимости описывается неравенством |z|>1
Правило: если область сходимости включает в себя единичную окружность, то сходится соответствующий Фурье образ. Верно и обратное: если единичная окружность не входит в область сходимости, то Фурье образ не сходится
Z преобразование наиболее полезно и замечательно, когда бесконечная степенная функция Х(z) может быть выражена в виде компактного полинома X(z)= 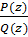 где P(z) и Q(z) – многочлены переменной z. Значения z, при которых Х(z) обращается в ноль, называют нулями, а значения z, при которых Х(z) обращается в бесконечность – полюсами.
где P(z) и Q(z) – многочлены переменной z. Значения z, при которых Х(z) обращается в ноль, называют нулями, а значения z, при которых Х(z) обращается в бесконечность – полюсами.
Полюса рациональной функции Х(z), расположенные в конечной области комплексной плоскости, совпадают с нулями знаменателя Q(z). Кроме того, полюса могут появляться в точках z=0 и z= 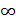 .
.
По расположению полюсов можно судить об области сходимости соответствующего ряда
Свойства области сходимости
1 свойство: область сходимости – это кольцо или круг с центром в нуле
2 свойство: преобразование Фурье последовательности x[n] сходится тогда и только тогда, когда область сходимости Z преобразования этой последовательности содержит единичную окружность
3 свойство: ОС не может содержать ни одного полюса
4 свойство: ОС Z преобразования конечного сигнала (сигнала с ненулевыми отсчетами, расположенными в конечном интервале) – вся комплексная плоскость, за исключением, быть может, z=0 и z= 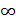 .
.
5 свойство: область сходимости правосторонней последовательности – последовательности с нулевыми отсчетами при n<N< 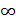 , представляет собой «внешность» круга с центром в нуле, на границе которого расположен полюс функции Х(z) с максимальным модулем
, представляет собой «внешность» круга с центром в нуле, на границе которого расположен полюс функции Х(z) с максимальным модулем
6 свойство: область сходимости левосторонней последовательности – последовательности с нулевыми отсчетами при - 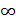 <N<n представляет собой «внутренность» круга с центром в нуле (возможно вместе с центром), на границе которого расположен полюс функции Х(z) с минимальным модулем
<N<n представляет собой «внутренность» круга с центром в нуле (возможно вместе с центром), на границе которого расположен полюс функции Х(z) с минимальным модулем
7 свойство: область сходимости двусторонней последовательности (т.е. не являющейся ни правой ни левой) представляет собой кольцо с центром в нуле, на границах которого расположены полюсы функции, а внутри кольца их нет
8 свойство: область сходимости должна быть связной (любые две точки можно соединить кривой, целиком лежащей в этой области)
Пример. Правосторонняя экспоненциальная последовательность
Рассмотрим сигнал x[n]=anu[n]. Так как его ненулевые отсчеты могут быть только при n>0, это правосторонняя последовательность.
Z-преобразование такой последовательности имеет вид
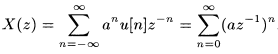
Для сходимости достаточно неравенства
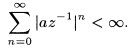
Таким образом, в область сходимости входят те значения z, для которых
|az-1|<1 или, что тоже самое, |z|>|a|
Внутри области сходимости, ряд сходится к функции
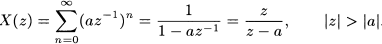
Тут мы воспользовались формулой суммы геометрической прогрессии.
ОС z-преобразования не пуста для любого конечного значения |a|. С другой стороны, Фурье –образ этой последовательности определен лишь для a c |a|<1. Если a=1 то последовательность превращается в единичный скачек с z-преобразованием
|
из
5.00
|
Обсуждение в статье: Свойства области сходимости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

