 |
Главная |
КОНЦЕНТРАЦИЯ НОСИТЕЛЕЙ
|
из
5.00
|
В собственном полупроводнике концентрации свободных электронов и дырок одинаковы:  . Подставляя
. Подставляя 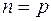 в формулу (1-8), легко получаем концентрации свободных электронов и дырок в собственном полупроводнике:
в формулу (1-8), легко получаем концентрации свободных электронов и дырок в собственном полупроводнике:
 (1-15).
(1-15).
Равенству концентраций 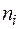 и
и  соответствует на рис. 1-5 идентичность кривых, характеризующих концентрацию свободных носителей в соответствующей разрешенной зоне.
соответствует на рис. 1-5 идентичность кривых, характеризующих концентрацию свободных носителей в соответствующей разрешенной зоне.
Зависимость собственных концентраций 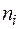 и
и  от температуры очень сильна и обусловлена в основном изменением температурного потенциала в показателе экспоненты, а не степенным множителем Т3/2. Столь же сильно зависит собственная концентрация от ширины запрещенной зоны при данной температуре. Так, сравнительно небольшое различие в значении
от температуры очень сильна и обусловлена в основном изменением температурного потенциала в показателе экспоненты, а не степенным множителем Т3/2. Столь же сильно зависит собственная концентрация от ширины запрещенной зоны при данной температуре. Так, сравнительно небольшое различие в значении  у германия и кремния (0,67 и 1,11 В) приводит к различию собственных концентраций при комнатной температуре более чем на 3 порядка. Сравнивая (1-8) и (1-15), соотношение (1-8) можно записать в более компактной форме:
у германия и кремния (0,67 и 1,11 В) приводит к различию собственных концентраций при комнатной температуре более чем на 3 порядка. Сравнивая (1-8) и (1-15), соотношение (1-8) можно записать в более компактной форме:
 (1-16)
(1-16)
которую и будем использовать в дальнейшем.
Используя формулы (1-16) и (1-7) и полагая  , нетрудно выразить концентрации
, нетрудно выразить концентрации  и
и  через собственную концентрацию
через собственную концентрацию 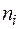 :
:
 , (1-17,a)
, (1-17,a)
 (1-17,б)
(1-17,б)
Отсюда легко получить потенциал Ферми в двух формах:
 ; (1-18,а)
; (1-18,а)
 . (1-18,б)
. (1-18,б)
Для того чтобы определить потенциал 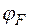 по формулам (1-10) или (1-18), нужно знать концентрации свободных носителей.
по формулам (1-10) или (1-18), нужно знать концентрации свободных носителей.
При оценке значений  и
и  используют условие нейтральности (точнее, квазинейтральности) полупроводника. Это важное условие формулируется следующим образом: в однородном полупроводнике не может быть существенных объемных некомпенсированных зарядов ни в равновесном состоянии, ни при наличии тока.
используют условие нейтральности (точнее, квазинейтральности) полупроводника. Это важное условие формулируется следующим образом: в однородном полупроводнике не может быть существенных объемных некомпенсированных зарядов ни в равновесном состоянии, ни при наличии тока.
Поэтому в общем виде условие нейтральности для единичного объема записывают так:
 (1-19,а)
(1-19,а)
где  ,
, 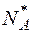 — концентрации ионизированных доноров и акцепторов. Уравнение (1-19а) говорит о том, что концентрация частиц, несущих положительный заряд (дырки и ионизированные доноры), равна концентрации частиц, несущих отрицательный заряд (электроны и ионизированные акцепторы).
— концентрации ионизированных доноров и акцепторов. Уравнение (1-19а) говорит о том, что концентрация частиц, несущих положительный заряд (дырки и ионизированные доноры), равна концентрации частиц, несущих отрицательный заряд (электроны и ионизированные акцепторы).
Для электронных полупроводников, не содержащих акцепторов,
 . (1-19,б)
. (1-19,б)
Для дырочных полупроводников, не содержащих доноров,
 (1-19,в)
(1-19,в)
Перейдем непосредственно к оценке концентраций свободных носителей. Рассмотрим сначала электронные полупроводники. В типичном электронном полупроводнике выполняется неравенство  . Кроме того, в рабочем диапазоне температур донорные атомы практически полностью ионизированы, т. е.
. Кроме того, в рабочем диапазоне температур донорные атомы практически полностью ионизированы, т. е.  . Тогда из соотношения (1-19,6) получаем концентрацию свободных электронов
. Тогда из соотношения (1-19,6) получаем концентрацию свободных электронов
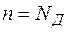 , (1-20,а)
, (1-20,а)
которая, как видим, определяется концентрацией примеси и, следовательно, не зависит от температуры. С помощью (1-16) легко получаем концентрацию свободных дырок
 , (1-20,б)
, (1-20,б)
которая согласно (1-15) очень сильно — экспоненциально — зависит от температуры. Наконец, из (1-18,а) или (1-13,а) находим уровень Ферми в типичном электронном полупроводнике:
 . (1-20,в)
. (1-20,в)
Простые формулы (1-20) широко используются на практике. Однако следует иметь в виду, что они действительны в ограниченном температурном диапазоне: с понижением температуры степень ионизации доноров уменьшается и принятое равенство  становится менее строгим. С повышением температуры увеличивается концентрация собственных носителей и постепенно нарушается принятое неравенство
становится менее строгим. С повышением температуры увеличивается концентрация собственных носителей и постепенно нарушается принятое неравенство  (электронный полупроводник превращается в собственный) .
(электронный полупроводник превращается в собственный) .
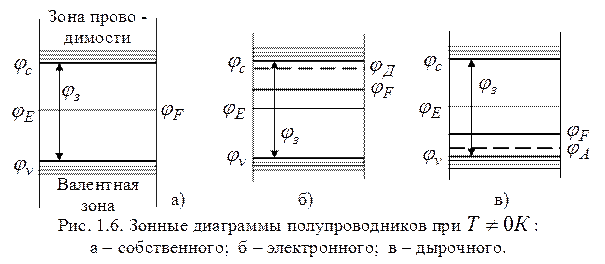
Случай дырочного полупроводника, в котором  , нет необходимости рассматривать столь же подробно. Главные особенности акцепторной примеси видны из рис. 1-6. Если акцепторы полностью ионизированы и температура ниже критической, то вместо формул (1-20) получаем аналогичные соотношения, характерные для ярко выраженного дырочного полупроводника:
, нет необходимости рассматривать столь же подробно. Главные особенности акцепторной примеси видны из рис. 1-6. Если акцепторы полностью ионизированы и температура ниже критической, то вместо формул (1-20) получаем аналогичные соотношения, характерные для ярко выраженного дырочного полупроводника:
 , (1-21,а)
, (1-21,а)
 , (1-21,б)
, (1-21,б)
 . (1-21,в)
. (1-21,в)
Из выше сказанного можно сделать следующие выводы:
- в собственных полупроводниках, у которых  , уровень Ферми расположен в середине запрещенной зоны (рис. 1.6.а);
, уровень Ферми расположен в середине запрещенной зоны (рис. 1.6.а);
- в примесных полупроводниках, у которых  , уровень Ферми лежит в верхней половине запрещенной зоны (рис. 1.6.б) и тем выше, чем больше концентрация доноров и чем меньше температура;
, уровень Ферми лежит в верхней половине запрещенной зоны (рис. 1.6.б) и тем выше, чем больше концентрация доноров и чем меньше температура;
- в примесных полупроводниках, у которых  , уровень Ферми лежит в нижней половине запрещенной зоны (рис. 1.6.в) и тем ниже, чем больше концентрация акцепторов и чем меньше температура.
, уровень Ферми лежит в нижней половине запрещенной зоны (рис. 1.6.в) и тем ниже, чем больше концентрация акцепторов и чем меньше температура.
Все предыдущие зонные диаграммы соответствовали однородным полупроводникам, в которых примеси распределены равномерно. Разумеется, однородный полупроводник является некоторой идеализацией. Более того, часто специально создают неоднородность внутри кристалла в виде градиента концентрации примесей, что придает полупроводнику свойства, необходимые для ряда приборов. Посмотрим, каковы особенности неоднородных полупроводников.
|
|
Рис. 1-7. Зонные диаграммы неоднородного полупроводника (а) и однородного полупроводника при наличии внешнего электрического поля (б).
Пусть, например, в полупроводнике типа п концентрация доноров изменяется от  до
до  . Согласно (1-20,в) разность
. Согласно (1-20,в) разность  уменьшается с уменьшением концентрации
уменьшается с уменьшением концентрации  . Поскольку в равновесной системе уровень Ферми во всех ее частях одинаков, зонная диаграмма должна иметь такой вид, как на рис. 1-7, а. Электростатический потенциал
. Поскольку в равновесной системе уровень Ферми во всех ее частях одинаков, зонная диаграмма должна иметь такой вид, как на рис. 1-7, а. Электростатический потенциал 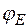 вдоль неоднородного полупроводника меняется. Следовательно, в неоднородных полупроводниках имеются внутренние электрические поля, в которых возможен дрейф носителей. Однако в отсутствие внешнего поля дрейфовые потоки носителей равны противоположно направленным диффузионным потокам тех же носителей, обусловленным градиентом их концентрации (в общем случае — градиентом химического потенциала). Поэтому результирующий поток отсутствует и соблюдается больцмановское равновесие.
вдоль неоднородного полупроводника меняется. Следовательно, в неоднородных полупроводниках имеются внутренние электрические поля, в которых возможен дрейф носителей. Однако в отсутствие внешнего поля дрейфовые потоки носителей равны противоположно направленным диффузионным потокам тех же носителей, обусловленным градиентом их концентрации (в общем случае — градиентом химического потенциала). Поэтому результирующий поток отсутствует и соблюдается больцмановское равновесие.
Для сравнения на рис. 1-7,б показана зонная диаграмма однородного полупроводника при наличии внешнего электрического поля (напряженность  та же, что и на рис. 1-7,а). Если в силу условия квазинейтральности принять концентрации носителей неизменными вдоль оси х, то будут неизменными и химические потенциалы, т. е. «расстояния» уровня
та же, что и на рис. 1-7,а). Если в силу условия квазинейтральности принять концентрации носителей неизменными вдоль оси х, то будут неизменными и химические потенциалы, т. е. «расстояния» уровня 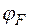 от краев разрешенных зон. Тогда согласно (1-18) получаем
от краев разрешенных зон. Тогда согласно (1-18) получаем  , т. е. имеет место градиент уровня Ферми, как и должно быть при нарушении равновесия (внешнее электрическое поле вызывает протекание тока). Наличие градиента уровня Ферми обусловливает принципиальное отличие данного случая от предыдущего (рис. 1-7,а) несмотря на внешнее сходство «перекошенных» зонных диаграмм.
, т. е. имеет место градиент уровня Ферми, как и должно быть при нарушении равновесия (внешнее электрическое поле вызывает протекание тока). Наличие градиента уровня Ферми обусловливает принципиальное отличие данного случая от предыдущего (рис. 1-7,а) несмотря на внешнее сходство «перекошенных» зонных диаграмм.
Заметим, что наличие внутреннего электрического поля, вообще говоря, означает нарушение условия квазинейтральности, однако если поле почти постоянное, то объемные заряды не существенны.
Все сказанное действительно и для полупроводника типа р с учетом специфики расположения уровня Ферми. Легко, например, убедиться, что при убывании концентрации акцепторов слева направо зоны искривляются не вверх, как на рис. 1-7,а, а вниз.
ПОДВИЖНОСТЬ НОСИТЕЛЕЙ
Удельная проводимость любого тела зависит не только от концентрации носителей, но и от их подвижности в электрическом поле. Подвижность носителей, по определению, есть их средняя направленная скорость в электрическом поле с напряженностью 1 В/см. Соответственно дрейфовую скорость можно записать в виде  .
.
Постоянство дрейфовой скорости носителей в однородном поле (  .) специфично для твердого тела, где имеются различные «препятствия» движению. В вакууме, где таких препятствий нет, движение заряженных частиц в однородном поле равноускоренное, т. е. понятие дрейфовой скорости отсутствует. Направленное движение, носителей в твердом теле под действием поля сочетается с их хаотическим (тепловым) движением. Последнее характеризуется средней тепловой скоростью
.) специфично для твердого тела, где имеются различные «препятствия» движению. В вакууме, где таких препятствий нет, движение заряженных частиц в однородном поле равноускоренное, т. е. понятие дрейфовой скорости отсутствует. Направленное движение, носителей в твердом теле под действием поля сочетается с их хаотическим (тепловым) движением. Последнее характеризуется средней тепловой скоростью
 , (1-22)
, (1-22)
зависящей от температуры. Если принять Т = 300 К и  , то
, то  .
.
При не слишком сильных электрических полях дрейфовая скорость намного меньше тепловой или, как говорят, температура носителей определяется температурой кристаллической решетки. В этих условиях подвижность можно выразить формулой
 (1-23)
(1-23)
где  - среднее время свободного пробега частицы;
- среднее время свободного пробега частицы;  - средняя длина ее свободного пробега (для кремния и германия
- средняя длина ее свободного пробега (для кремния и германия  и
и  ).
).
Величины  и
и  характеризуют частоту столкновений носителей с теми или иными «препятствиями». В результате таких столкновений происходит изменение скорости и направления движения носителей, т. е. их рассеяние. Теория показывает, что при нулевой абсолютной температуре в идеальной кристаллической решетке рассеяние не имеет места. Иначе говоря, атомы решетки как таковые не являются препятствием на пути движения носителей. Истинными препятствиями являются лишь колеблющиеся атомы решетки (в корпускулярной интерпретации — фононы), а также атомы примесей и дефекты структуры.
характеризуют частоту столкновений носителей с теми или иными «препятствиями». В результате таких столкновений происходит изменение скорости и направления движения носителей, т. е. их рассеяние. Теория показывает, что при нулевой абсолютной температуре в идеальной кристаллической решетке рассеяние не имеет места. Иначе говоря, атомы решетки как таковые не являются препятствием на пути движения носителей. Истинными препятствиями являются лишь колеблющиеся атомы решетки (в корпускулярной интерпретации — фононы), а также атомы примесей и дефекты структуры.
В области очень низких температур интенсивность тепловых колебаний мала, количество фононов незначительно и рассеяние обусловлено главным образом дефектами решетки и нейтральными примесями (нейтральность примесей является следствием низкой температуры, меньшей температуры ионизации).
В области обычных рабочих температур рассеяние обусловлено главным образом фононами и ионизированными примесями. В этой области подвижность 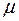 можно представить состоящей из двух компонентов
можно представить состоящей из двух компонентов 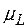 и
и  , связанных с результирующей подвижностью формулой
, связанных с результирующей подвижностью формулой
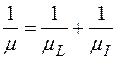 (1-24)
(1-24)
Очевидно, что результирующая подвижность определяется наименьшим из компонентов 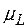 и
и 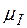 .
.
 |
 Анализ показывает, что при решеточном рассеянии
Анализ показывает, что при решеточном рассеянии  . Тогда из (1-23) с учетом (1-22) следует соотношение
. Тогда из (1-23) с учетом (1-22) следует соотношение
 . (1-25,а)
. (1-25,а)
При ионном рассеянии получается соотношение
 , (1-25,6)
, (1-25,6)
где N — концентрация ионизированной однозарядной примеси.
Для кремния при температуре  меньшей оказывается составляющая
меньшей оказывается составляющая 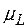 ; поэтому зависимость
; поэтому зависимость  описывается выражением (1-25а): подвижность уменьшается с ростом температуры. При температуре
описывается выражением (1-25а): подвижность уменьшается с ростом температуры. При температуре  меньшей оказывается составляющая
меньшей оказывается составляющая 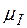 ; поэтому зависимость
; поэтому зависимость  описывается выражением (1-25,б): подвижность уменьшается с уменьшением температуры.
описывается выражением (1-25,б): подвижность уменьшается с уменьшением температуры.
Из соотношений (1-25) видно, что подвижности  и
и  , а следовательно, и результирующая подвижность
, а следовательно, и результирующая подвижность  , обратно пропорциональны эффективной массе. Этим, в частности, объясняется различие подвижностей электронов и дырок. Как правило,
, обратно пропорциональны эффективной массе. Этим, в частности, объясняется различие подвижностей электронов и дырок. Как правило,  . Если воспользоваться общепринятым обозначением
. Если воспользоваться общепринятым обозначением
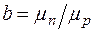 , (1-26)
, (1-26)
то получим: для кремния b= 2,8 и для германия b = 2,1.
Соотношения (1-25) позволяют исследовать зависимость подвижности от температуры и концентрации примеси.
 Зависимость
Зависимость  оказывает непосредственное влияние на вольт-амперную характеристику полупроводника. Например, в простейшем случае (однородный кристалл с постоянным сечением) ток I пропорционален скорости
оказывает непосредственное влияние на вольт-амперную характеристику полупроводника. Например, в простейшем случае (однородный кристалл с постоянным сечением) ток I пропорционален скорости 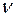 , анапряжение
, анапряжение  — напряженности электрического поля
— напряженности электрического поля  ,поэтому форма кривой
,поэтому форма кривой  такая же, как кривой
такая же, как кривой  (рис. 1-14). На начальном участке соблюдается закон Ома, поскольку
(рис. 1-14). На начальном участке соблюдается закон Ома, поскольку  и, следовательно,
и, следовательно,  . На последующих двух участках этот закон все больше нарушается, вплоть до насыщения тока. Значит, при достаточно больших напряжениях (когда поле Е > Екр) полупроводник ведет себя как нелинейный резистор.
. На последующих двух участках этот закон все больше нарушается, вплоть до насыщения тока. Значит, при достаточно больших напряжениях (когда поле Е > Екр) полупроводник ведет себя как нелинейный резистор.
|
из
5.00
|
Обсуждение в статье: КОНЦЕНТРАЦИЯ НОСИТЕЛЕЙ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы



