 |
Главная |
УДЕЛЬНАЯ ПРОВОДИМОСТЬ И УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ
|
из
5.00
|
Движение носителей в электрическом поле называют дрейфом. Плотность дрейфового тока определяется выражением  где
где  - удельная проводимость.
- удельная проводимость.
В общем виде удельная проводимость выражается следующим образом
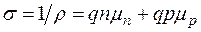 , (1-27)
, (1-27)
где  - подвижности электронов и дырок;
- подвижности электронов и дырок;  - удельное сопротивление.
- удельное сопротивление.
Для частных случаев собственного, электронного и дырочного полупроводников получаем соответственно:
 ; (1-28)
; (1-28)
 ; (1-29)
; (1-29)
 . (1-30)
. (1-30)
Температурную зависимость удельной проводимости или удельного сопротивления можно получить, зная температурную зависимость концентрации носителей и их подвижности.
На рис. 1.21 показаны зависимости удельной проводимости разных типов полупроводников при изменении температуры.
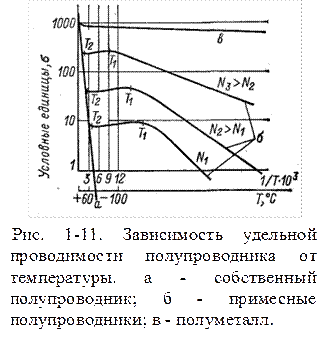

В широком температурном диапазоне зависимость  удобно изображать в полулогарифмическом масштабе, откладывая по оси абсцисс «обратную температуру»
удобно изображать в полулогарифмическом масштабе, откладывая по оси абсцисс «обратную температуру» 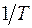 (рис. 1-11). В этом случае для собственного полупроводника получается прямая, наклон которой пропорционален
(рис. 1-11). В этом случае для собственного полупроводника получается прямая, наклон которой пропорционален  . Этот результат следует из выражения (1-28), если подставить в него (1-15).
. Этот результат следует из выражения (1-28), если подставить в него (1-15).
На рис. 1-12 для наглядности показана зависимость удельного сопротивления от температуры в линейном масштабе и в более узком диапазоне, характерном для применения в полупроводниковой технике.
1-9. РЕКОМБИНАЦИЯ НОСИТЕЛЕЙ
Общие сведения. Процессы генерации и рекомбинации носителей заряда неотъемлемы друг от друга и в то же время противоположны по содержанию. Генерация является ведущим началом в этом единстве и связана с воздействием таких внешних факторов, как нагрев, освещение или облучение. Рекомбинация представляет собой внутреннюю реакцию системы на появление и возрастание числа носителей. Именно рекомбинация, противодействуя накоплению носителей, обусловливает их равновесные концентрации. Поэтому изучение механизма рекомбинации и ее количественных закономерностей необходимо для понимания и использования многих важнейших явлений в полупроводниках и полупроводниковых приборах.
Непосредственная рекомбинация свободного электрона со свободной дыркой — сравнительно редкое событие. Время жизни носителей, вычисленное исходя из непосредственной рекомбинации, на несколько порядков больше наблюдаемых значений. Поэтому главную роль следует отвести механизму рекомбинации с помощью центров рекомбинации, которые часто называют «ловушками». Напомним, что ловушке свойственны энергетические уровни, расположенные глубоко в запрещенной зоне, близко к ее середине. Переход электрона из зоны проводимости на уровень ловушки и затем в валентную зону гораздо более вероятен, чем непосредственный переход через запрещенную зону при непосредственной рекомбинации. На рис. 1-23 показаны две возможные последовательности процессов при рекомбинации на ловушках.  Поскольку ловушка в равной степени облегчает переход электронов как из зоны проводимости в валентную зону, так и в обратном направлении, она представляет собой не только центр рекомбинации, но и центр генерации носителей, как и должно быть из общих соображений о равновесии. С физической точки зрения понятие ловушек столь же широко, как и понятие примесей; это могут быть и посторонние атомы, и различные подвижные частицы, и дефекты кристаллической решетки. Для изготовления германиевых и кремниевых диодов и транзисторов, как правило, используют монокристаллы с регулярной структурой, у которых время жизни обычно лежит в пределах10 – 100 мксек.
Поскольку ловушка в равной степени облегчает переход электронов как из зоны проводимости в валентную зону, так и в обратном направлении, она представляет собой не только центр рекомбинации, но и центр генерации носителей, как и должно быть из общих соображений о равновесии. С физической точки зрения понятие ловушек столь же широко, как и понятие примесей; это могут быть и посторонние атомы, и различные подвижные частицы, и дефекты кристаллической решетки. Для изготовления германиевых и кремниевых диодов и транзисторов, как правило, используют монокристаллы с регулярной структурой, у которых время жизни обычно лежит в пределах10 – 100 мксек.
Для анализа и расчета полупроводниковых приборов чаще всего используют единый параметр – так называемое эффективное время жизни 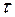 , которое характеризует совместное влияние объемной и поверхностной рекомбинации и определяется соотношением
, которое характеризует совместное влияние объемной и поверхностной рекомбинации и определяется соотношением
 , (1-31)
, (1-31)
где  и
и  - объемное и поверхностное времена жизни.
- объемное и поверхностное времена жизни.
1-10. ЗАКОНЫ ДВИЖЕНИЯ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКАХ
В общем случае движение носителей заряда в полупроводниках обусловлено двумя процессами: диффузией под действием градиента концентрации и дрейфом под действием градиента потенциала в электрическом поле. Поскольку в полупроводниках мы имеем дело с двумя типами носителей — дырками и электронами, полная плотность тока состоит из четырех составляющих :
 , (1-32)
, (1-32)
где индексы «диф» и «др» относятся соответственно к диффузионной и дрейфовой составляющим плотности токов.
Плотности дрейфовых составляющих тока пропорциональны градиенту электрического потенциала  , т. е. напряженности электрического поля
, т. е. напряженности электрического поля  . В одномерном случае, когда движение носителей происходит только вдоль оси х, без отклонения в стороны, имеем:
. В одномерном случае, когда движение носителей происходит только вдоль оси х, без отклонения в стороны, имеем:
 (1-33,а)
(1-33,а)
 (1-33,6)
(1-33,6)
Следует заметить, что в обычном соотношении  использованном в формулах (1-33), потенциал
использованном в формулах (1-33), потенциал  относится к положительным зарядам, тогда как на зонных диаграммах величина
относится к положительным зарядам, тогда как на зонных диаграммах величина  характеризует энергию отрицательных зарядов — электронов. Поэтому для зонных диаграмм действительно соотношение
характеризует энергию отрицательных зарядов — электронов. Поэтому для зонных диаграмм действительно соотношение  , т. е. положительной напряженности поля соответствует положительный градиент энергетических уровней.
, т. е. положительной напряженности поля соответствует положительный градиент энергетических уровней.
Плотности диффузионных составляющих тока пропорциональны градиентам химических потенциалов 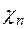 и
и  , которые для невырожденных полупроводников выражаются формулами (1-12). Поэтому в одномерном случае имеем :
, которые для невырожденных полупроводников выражаются формулами (1-12). Поэтому в одномерном случае имеем :
 ; (1-34,а)
; (1-34,а)
 . (1-34,6)
. (1-34,6)
Здесь  и
и  — коэффициенты диффузии дырок и электронов, связанные с подвижностями тех же носителей формулой Эйнштейна
— коэффициенты диффузии дырок и электронов, связанные с подвижностями тех же носителей формулой Эйнштейна
 . (1-35)
. (1-35)
Знак минус в формуле (1-33а) имеет следующий физический смысл: диффузия всегда происходит в направлении убывания концентрации, а поскольку дырки несут положительный заряд, ток 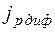 должен быть положительным при
должен быть положительным при  .
.
Из выражений (1-33) следует, что в невырожденных полупроводниках, для которых действительны использованные значения химических потенциалов, диффузионные токи пропорциональны градиенту концентраций носителей, а коэффициенты диффузии не зависят от этих концентраций. Подставляя (1-32) и (1-33) в формулу (1-31), получаем плотность полного тока:
 (1-36)
(1-36)
Как видим, для определения тока необходимо знать концентрации носителей и напряженность поля. В общем случае концентрации р и п зависят от двух переменных: координаты  и времени
и времени  . Поэтому для определения токов нужно предварительно найти функции
. Поэтому для определения токов нужно предварительно найти функции  и
и  . Эти функции являются решениями так называемых уравнений непрерывности потока, которым в любой момент времени подчиняется движение носителей.
. Эти функции являются решениями так называемых уравнений непрерывности потока, которым в любой момент времени подчиняется движение носителей.
Для дырок и электронов уравнения непрерывности записываются в следующем виде :
 ; (1-37,а)
; (1-37,а)
 , (1-37,6)
, (1-37,6)
где  и
и 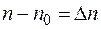 — избыточные концентрации;
— избыточные концентрации;  и
и 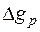 — скорости генерации под действием внешних факторов, например света.
— скорости генерации под действием внешних факторов, например света.
Слагаемые в правых частях (1-37) соответствуют возможным причинам изменения концентрации носителей во времени. В частности, последние слагаемые можно рассматривать как скорости накопления или рассасывания носителей, обусловленные неравенством потоков, втекающих и вытекающих из некоторого элементарного объема. Такой небаланс потоков характеризуется дивергенцией вектора плотности потока. В нашем случае плотность потока есть  . Дивергенция этого вектора в одномерном случае равна:
. Дивергенция этого вектора в одномерном случае равна:
 .
.
Подставляя сюда соотношения (1-33) и (1-34), получаем:
 ;
;
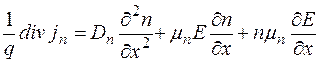 .
.
С учетом этих выражений, а также при отсутствии внешних факторов (свет, радиация и т. п.) уравнения непрерывности (1-37) принимают следующую форму:
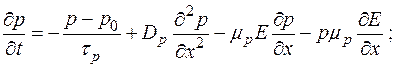 (1-38,а)
(1-38,а)  (1-38,6)
(1-38,6)
Из этих уравнений следует вывод.
Изменение концентраций носителей заряда в полупроводнике с течением времени происходит из-за их рекомбинации (первые члены правых частей), перемещений вследствие диффузии (вторые члены), и дрейфа (третьи и четвертые члены).
В том случае, когда поле отсутствует или когда его ролью заведомо можно пренебречь, полагаем Е = 0. При этом выражения (1-38) упрощаются и носят название уравнений диффузии:
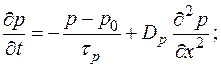 (1-39,а)
(1-39,а)
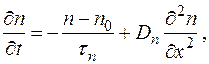 (1-39,6)
(1-39,6)
Уравнения (1-39) позволяют достаточно строго анализировать многие типы полупроводниковых приборов.
В тех случаях, когда полем пренебречь нельзя, пользуются полными уравнениями (1-38). Если напряженность Е меняется вдоль оси  (т. е. если в полупроводнике имеется существенный объемный заряд), приходится дополнительно привлекать уравнение Пуассона, которое в одномерном случае имеет вид:
(т. е. если в полупроводнике имеется существенный объемный заряд), приходится дополнительно привлекать уравнение Пуассона, которое в одномерном случае имеет вид:
 , (1-40)
, (1-40)
где 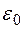 — электрическая постоянная (диэлектрическая проницаемость вакуума);
— электрическая постоянная (диэлектрическая проницаемость вакуума);  — относительная диэлектрическая проницаемость;
— относительная диэлектрическая проницаемость;  — плотность заряда.
— плотность заряда.
В общем случае
 . (1-41,a)
. (1-41,a)
Поскольку в условиях нейтральности  , можно считать, что объемный заряд есть следствие приращения концентраций в правой части (1-41а). Если степень ионизации примесей неизменна (т. е.
, можно считать, что объемный заряд есть следствие приращения концентраций в правой части (1-41а). Если степень ионизации примесей неизменна (т. е.  ), то
), то
 . (1-41,6)
. (1-41,6)
Решение системы уравнений (1-38) и (1-40) в общем виде невозможно. В каждом конкретном случае приходится вводить те или иные упрощения. В следующих параграфах рассматривается несколько примеров таких упрощенных решений, которые одновременно позволят ознакомиться еще с некоторыми важными свойствами и параметрами полупроводников.
1-11 ОБЪЕМНЫЕ ЗАРЯДЫ И ПОЛЯ В ПОЛУПРОВОДНИКАХ
Диэлектрическая релаксация. Пусть в ограниченном объеме полупроводника удалось сосредоточить избыточные концентрации электронов и дырок, так что образовался объемный заряд с плотностью  . Под действием возникшего поля заряд будет рассасываться, т. е. носители будут покидать тот начальный объем, в котором они были сосредоточены. Такое рассасывание заряда под действием собственного поля носит название диэлектрической релаксации, или релаксации Максвелла.
. Под действием возникшего поля заряд будет рассасываться, т. е. носители будут покидать тот начальный объем, в котором они были сосредоточены. Такое рассасывание заряда под действием собственного поля носит название диэлектрической релаксации, или релаксации Максвелла.
При анализе диэлектрической релаксации пренебрегают рекомбинацией носителей и их диффузией, чтобы выделить явление в чистом виде. Следовательно, в правых частях (1-38) можно опустить все члены, кроме последних:

 .
.
Вычитая второе уравнение из первого, , подставляя  из (1-40),
из (1-40),  из (1-416) и учитывая (1-27) получаем уравнение релаксации:
из (1-416) и учитывая (1-27) получаем уравнение релаксации:
 . (1-42)
. (1-42)
Решением является экспоненциальная функция
 , (1-43)
, (1-43)
где 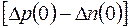 — начальная избыточная концентрация и
— начальная избыточная концентрация и
 (1-44)
(1-44)
— время диэлектрической релаксации.
 Величина
Величина 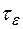 характеризует время, в течение которого нарушена нейтральность полупроводника: через (3-
характеризует время, в течение которого нарушена нейтральность полупроводника: через (3- 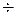 -4)
-4) 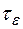 объемный заряд практически рассасывается и нейтральность восстанавливается.
объемный заряд практически рассасывается и нейтральность восстанавливается.
Как видно из (1-44), время релаксации помимо диэлектрической проницаемости зависит от удельной проводимости или удельного сопротивления. Например, если  , то для германия и кремния
, то для германия и кремния 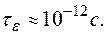 Такое крайне малое значение типично для процессов диэлектрической релаксации и является одной из основ квазинейтральности полупроводников.
Такое крайне малое значение типично для процессов диэлектрической релаксации и является одной из основ квазинейтральности полупроводников.
С ростом удельного сопротивления время релаксации увеличивается и у собственных полупроводников (особенно кремния) должно, казалось бы, достигать сравнительно больших значений. Следует, однако, иметь в виду, что наличие избыточных электронов и дырок в возмущенном объеме приводит к уменьшению удельного сопротивления на этом участке и, следовательно, согласно (1-44) способствует уменьшению времени релаксации. Поэтому даже в собственных полупроводниках при сколько-нибудь значительных возмущениях значение те обычно имеет порядок  с.
с.
Изменение удельного сопротивления полупроводника на том участке, где по тем или иным причинам скапливаются избыточные носители, носит название эффекта модуляции проводимости. Этот эффект играет значительную роль в полупроводниковых приборах, особенно при больших сигналах.
Из структуры выражения (1-43) следует важный вывод о двух вариантах механизма релаксации. А именно, предположим, что полупроводник дырочный и в нем создано начальное возмущение  при
при  . Тогда, поскольку электронов в окружающем объеме очень мало и они не могут нейтрализовать (скомпенсировать) возмущение
. Тогда, поскольку электронов в окружающем объеме очень мало и они не могут нейтрализовать (скомпенсировать) возмущение  , релаксация будет состоять в уменьшении концентрации
, релаксация будет состоять в уменьшении концентрации 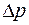 благодаря уходу избыточных дырок из начального объема. Процесс рассасывания будет описываться выражением
благодаря уходу избыточных дырок из начального объема. Процесс рассасывания будет описываться выражением

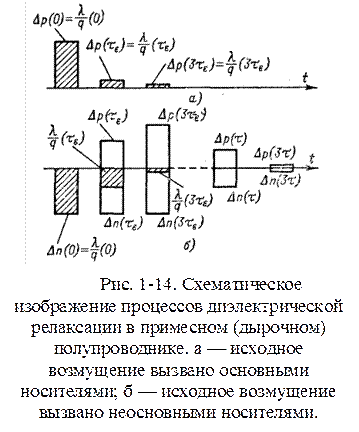
и закончится через время, равное примерно  (рис. 1-14, а).
(рис. 1-14, а).
Предположим теперь, что в том же дырочном полупроводнике начальное возмущение представляет собой избыточную концентрацию электронов  при
при 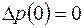 . Тогда релаксация будет состоять в нейтрализации (компенсации) заряда электронов
. Тогда релаксация будет состоять в нейтрализации (компенсации) заряда электронов  дырками, приходящими под действием поля из внешнего объема, где их очень много. Процесс нейтрализации описывается выражением
дырками, приходящими под действием поля из внешнего объема, где их очень много. Процесс нейтрализации описывается выражением
 , (1-45)
, (1-45)
т. е. характеризуется увеличением концентрации  до
до  и заканчивается, как и в первом случае, через
и заканчивается, как и в первом случае, через  . После этого с гораздо меньшей скоростью, определяемой временем жизни
. После этого с гораздо меньшей скоростью, определяемой временем жизни 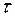 носителей заряда будет происходить рекомбинация электронов и дырок, скопившихся в области возмущения (рис. 1-14, б).
носителей заряда будет происходить рекомбинация электронов и дырок, скопившихся в области возмущения (рис. 1-14, б).
Таким образом, если возмущение было вызвано основными носителями заряда, то рассасывание их произойдет за малый промежуток времени. Если возмущение вызвано не основными для данного полупроводника носителями заряда, то в течение короткого времени в полупроводнике появится дополнительный заряд основных носителей, компенсирующий заряд неосновных носителей.
Если возмущение, в результате которого появилась дополнительная концентрация носителей заряда в полупроводнике, закончилось, то эти заряды в результате рекомбинации рассасываются, причем их концентрация убывает до равновесной по экспоненциальному закону
 , (1-46)
, (1-46)
где  - концентрации носителей заряда в момент прекращения возмущения и окончания процесса нейтрализации;
- концентрации носителей заряда в момент прекращения возмущения и окончания процесса нейтрализации; 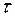 - время жизни носителей заряда.
- время жизни носителей заряда.
Время жизни носителей заряда 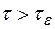 , поэтому рассасывание заряда происходит значительно дольше, чем его нейтрализация.
, поэтому рассасывание заряда происходит значительно дольше, чем его нейтрализация.
1-12. КИНЕТИКА НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКАХ
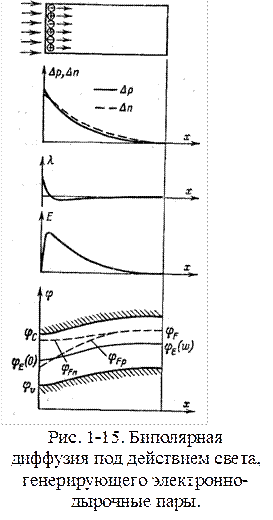
Биполярная диффузия. Пусть на поверхность полупроводника падает рассеянный пучок света (рис. 1-31). Тогда в тонком приповерхностном слое, в который проникает свет, будут генерироваться электронно-дырочные пары со скоростью 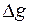 , пар/(см3-с). Между поверхностью и основным объемом возникнут градиенты концентрации электронов и дырок, и избыточные носители начнут диффундировать в глубь полупроводника. Такое совместное движение обоих типов носителей называют биполярной диффузией. Если бы подвижности (а значит, и коэффициенты диффузии) у электронов и дырок были одинаковы, то они двигались бы в виде единого нейтрального потока, который можно было бы анализировать с помощью одного из уравнений (1- 39). На самом деле подвижности носителей различны [см. (1-26)], поэтому у электронного потока будет тенденция «обогнать» дырочный поток. В результате взаимного сдвига потоков образуются небольшой объемный заряд и соответствующее электрическое поле, которое тормозит поток электронов и ускоряет поток дырок. В конце концов, устанавливается стационарный режим, при котором избыточные электроны и дырки распределены в виде сдвинутых относительно друг друга «облачков». Эти «облачка» двигаются синхронно, так что результирующий ток отсутствует. Концентрация носителей в «облачках» спадает с удалением от поверхности благодаря рекомбинации. Описанные явления известны под названием эффекта Дембера, а электрическое поле и разность потенциалов, свойственные этому эффекту, называют демберовским полем и демберовским напряжением
, пар/(см3-с). Между поверхностью и основным объемом возникнут градиенты концентрации электронов и дырок, и избыточные носители начнут диффундировать в глубь полупроводника. Такое совместное движение обоих типов носителей называют биполярной диффузией. Если бы подвижности (а значит, и коэффициенты диффузии) у электронов и дырок были одинаковы, то они двигались бы в виде единого нейтрального потока, который можно было бы анализировать с помощью одного из уравнений (1- 39). На самом деле подвижности носителей различны [см. (1-26)], поэтому у электронного потока будет тенденция «обогнать» дырочный поток. В результате взаимного сдвига потоков образуются небольшой объемный заряд и соответствующее электрическое поле, которое тормозит поток электронов и ускоряет поток дырок. В конце концов, устанавливается стационарный режим, при котором избыточные электроны и дырки распределены в виде сдвинутых относительно друг друга «облачков». Эти «облачка» двигаются синхронно, так что результирующий ток отсутствует. Концентрация носителей в «облачках» спадает с удалением от поверхности благодаря рекомбинации. Описанные явления известны под названием эффекта Дембера, а электрическое поле и разность потенциалов, свойственные этому эффекту, называют демберовским полем и демберовским напряжением
Значения демберовского поля и демберовского напряжения можно оценить из условия нулевого результирующего тока. Полагая  в формуле (1-36) и используя соотношение (1-27), получаем:
в формуле (1-36) и используя соотношение (1-27), получаем:
 . (1-47)
. (1-47)
 |
В заключение отметим, что биполярная диффузия, несмотря на отсутствие результирующего тока, является неравновесным процессом, так как имеются потоки носителей. Поэтому уровень Ферми не будет в данном случае постоянным, во всяком случае, в той области, где потоки еще существенны и где повышены концентрации обоих типов носителей. В этих областях (см. рис. 1-15) уровень Ферми «расщепляется» на два квазиуровня — один для электронов, другой для дырок.
Монополярная диффузия. Выше при анализе биполярной диффузии предполагалось, что оба типа носителей вводятся одновременно и в равных количествах. Поэтому «автоматически» обеспечивалась квазинейтральность, а результирующий ток отсутствовал.
Предположим теперь, что в приповерхностный слой полупроводника вводится (инжектируется) только один тип носителей - неосновных (рис. 1-16). Пусть для определенности осуществляется инжекция дырок в электронный полупроводник. Инжектированные дырки благодаря градиенту концентрации будут диффундировать в глубь кристалла, т. е. появится дырочный ток. Заряд дырок практически мгновенно (со временем диэлектрической релаксации) будет компенсирован таким же зарядом электронов, притягиваемых из глубоких слоев (необходимое количество дополнительных электронов поступает из внешней цепи, по которой протекает ток). В результате вблизи инжектирующей поверхности образуется квазинейтральное электронно-дырочное «облачко», почти такое же, как при биполярной диффузии (ср. рис. 1-15 и 1-16). Образуется также демберовское поле. Процесс, при котором диффундируют носители одного типа, а носители другого типа лишь обеспечивают квазинейтральность, называют монополярной диффузией.
Несмотря на внешнее сходство в распределении носителей монополярная диффузия принципиально отличается от биполярной диффузии. Отличия состоят в следующем:
1. Имеется результирующий ток; поэтому, в частности, полупроводник должен быть элементом замкнутой цепи Соответственно помимо демберовского поля, сосредоточенного вблизи инжектирующей поверхности, во всей толще полупроводника действует «обычное» — омическое поле, обусловленное приложенным напряжением.
2. Потоки дырок и электронов направлены в разные стороны: дырки двигаются в глубь кристалла, а электроны — в сторону инжектирующей поверхности, в район электронно-дырочного «облачка», где происходит интенсивная рекомбинация и необходимо пополнение основных носителей. Результирующий ток является суммой дырочной и электронной составляющих.
3. В связи с постоянством результирующего тока дырочная и электронная составляющие меняются в разные стороны. Убывание дырочного тока от поверхности в глубь кристалла сопровождается соответствующим ростом электронной составляющей. На самой инжектирующей поверхности электронный ток равен нулю, так как близко к нулю электрическое поле. Следовательно, в непосредственной близости от инжектирующей поверхности ток обусловлен только дырками. В глубине кристалла, где дырочный ток благодаря рекомбинации делается равным нулю, обращается в нуль и диффузионная составляющая электронного тока. Следовательно, вдали от инжектирующей поверхности ток обусловлен только электронами и имеет чисто дрейфовый характер: электроны двигаются в омическом поле, созданном внешним напряжением. Указанные отличия принципиальны с физической точки зрения. С математической же точки зрения распределения  и
и  описываются либо уравнением биполярной диффузии (если полупроводник близок к собственному), либо (в случае электронного полупроводника) уравнением (1-38а).
описываются либо уравнением биполярной диффузии (если полупроводник близок к собственному), либо (в случае электронного полупроводника) уравнением (1-38а).
Что касается выражения для поля 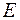 ,то оно в данном случае будет отличаться от (1-47), поскольку результирующий ток не равен нулю. Подставляя (1-33) и (1-34) в (1-32), легко получить:
,то оно в данном случае будет отличаться от (1-47), поскольку результирующий ток не равен нулю. Подставляя (1-33) и (1-34) в (1-32), легко получить:
 (1-48)
(1-48)
Сравнивая (1-47) с (1-48), замечаем, что поле при монополярной диффузии складывается из постоянной (омической) и демберовской составляющих. Строгое решение задачи о распределении носителей при монополярной диффузии затруднительно. Поэтому решим эту задачу для малых возмущений и в диффузионном приближении. Величину возмущения принято характеризовать уровнем инжекции

т. е отношением концентрации избыточных носителей к равновесной концентрации основных носителей. Малому возмущению соответствует неравенство 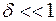 , т. е.
, т. е.
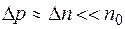 (1-49)
(1-49)
которое называют условием низкого уровня инжекции.Диффузионное приближение характеризуется тем, что в уравнении непрерывности пренебрегают членом с  и тогда можно воспользоваться диффузионным уравнением (1-39а).
и тогда можно воспользоваться диффузионным уравнением (1-39а).
Поделив обе части (1-39а) на  ,запишем стационарный вариант диффузионного уравнения в следующем виде:
,запишем стационарный вариант диффузионного уравнения в следующем виде:
 (1-50)
(1-50)
Величина 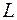 (индекс для общности опущен) определяется выражением
(индекс для общности опущен) определяется выражением
 ; (1-51)
; (1-51)
она имеет размерность длины и носит название средней диффузионной длины или средней длины диффузии.Физический смысл величины  будет ясен из дальнейшего.
будет ясен из дальнейшего.
Остановимся сначала на стационарном уравнении (1-50). Как известно, его решение является суммой двух экспонент:
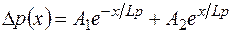 (1-52)
(1-52)
где коэффициенты 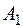 и
и  определяются из граничных условий (обычно при
определяются из граничных условий (обычно при 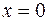 и
и  ). Если
). Если  и
и  , то
, то 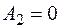 и
и  . Тогда
. Тогда
 (1-53)
(1-53)
т. е. избыточные концентрации, спадают по экспоненте. Это один из характерных случаев в теории полупроводниковых приборов.
Из выражения (1-53) следует, что диффузионная длина есть то расстояние, на котором концентрация диффундирующих носителей(при их экспоненциальном распределении) уменьшается в е раз.На участке длиной  концентрация уменьшается в 20—50 раз, т. е. становится пренебрежимо малой по сравнению с исходной.
концентрация уменьшается в 20—50 раз, т. е. становится пренебрежимо малой по сравнению с исходной.
Можно показать, что при экспоненциальном распределении носителей их диффузионная скорость является постоянной величиной, равной
 .
.
Исходя из последнего выражения, можно дать еще одно определение величины  : диффузионная длина есть то среднее расстояние, которое носители в процессе диффузии проходят за время жизни.
: диффузионная длина есть то среднее расстояние, которое носители в процессе диффузии проходят за время жизни.
|
из
5.00
|
Обсуждение в статье: УДЕЛЬНАЯ ПРОВОДИМОСТЬ И УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

