Координаты профиля третьего (среднего) сечения лопасти

Таблица 2.5

Размерная хорда при R = 2,0 м = 2000мм

Номер сечения	1 (корень)	2	3 (середина)	4	5 (периферия)
bk, мм	240	220	200	180	160

Толщина профиля

Толщина профиля k -го сечения (см. формулу (1.37)) . Для 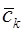, определенного по (1.26), пр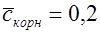и  и  для пяти сечений результат приведен в табл. 2.6.

Таблица 2.6

Относительная толщина, построенная по корневому
и периферийному сечениям

Номер сечения	1 (корень)	2	3 (середина)	4	5 (периферия)
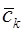
	0,200	0,182	0,160	0,133	0,100

Уточнение относительной толщины профиля

Ниже уточним 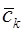, перейдя к построению линейчатой лопасти с заданным средним и периферийным сечениями.

Поскольку  изменяется по линейному закону, то, приняв величину  на серединном сечении и на периферии такую же, как и в табл. 2.4, и подчинив  соотношению (1.39), получим те же значения, что и в табл. 2.4. Относительную толщину профиля строим по следующим значениям для среднего и периферийного сечений:

Тогда для остальных сечений в соответствии с выражениями (1.40)
и (1.41)

 ,

где

 .

При  и  и значениях  для всех пяти сечений, данных в табл. 2.4, имеем величины 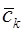 и приводим их в табл. 2.7.

Таблица 2.7

Относительная толщина, построенная по среднему и периферийному
сечениям, и вспомогательный множитель S_k

Номер сечения	1 (корень)	2	3 (середина)	4	5 (периферия)
Sk	– 1,0	– 0,5	0,0	0,5	1,0
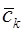
	0,183	0,168	0,150	0,128	0,100

Из табл. 2.7 видно, что величина  задана в среднем сечении, что обеспечивает профиль пятнадцатипроцентной толщины в этом сечении.

Размерные величины толщины профиля представлены в табл. 2.8.

Таблица 2.8

Размерные толщины профилей

Номер сечения	1 (корень)	2	3 (середина)	4	5 (периферия)
ck, мм	44,0	37,0	30,0	23,0	16,0

Из табл. 2.8 видно, что размерные величины толщин профилей, в отличие от безразмерных в долях хорды, ведут себя как линейная функция по высоте лопасти.

Координаты профилей

Для выбранного профиля типа "Эсперо" безразмерные координаты верхней  и нижней  дуг приведены в табл. 1.3.

С помощью пересчета для размерных хорд b_k и толщин c_k получаем таблицы размерных координат профилей.

Приводим табл. 2.9 и 2.10 координаты профилей для третьего (среднего) и пятого (периферийного) сечений, полученных по формулам (1.38)

; ;  

Для k = 3 (среднее сечение) — b₃ = 200 мм, c₃ = 30 мм.

Для k = 5 (периферийное сечение) — b₅ = 160 мм, c₅ = 16 мм.

Таблица 2.9

Координаты профиля третьего (среднего) сечения лопасти

Номер точки	x, мм	y в, мм	y н, мм
1	0	12,5	12,5
2	2,5	16,1	8,4
3	5,0	18,2	6,9
4	10,0	20,8	5,0
5	20,0	24,7	3,3
6	40,0	28,8	1,7
7	60,0	30,2	0,7
8	70,4	30,16	0,34
9	80,0	30,0	0,0

 

Окончание табл. 2.9

Номер точки	x, мм	y в, мм	y н, мм
10	100,0	28,4	0,0
11	120,0	25,0	0,0
12	140,0	20,8	0,0
13	160,0	15,3	0,0
14	180,0	9,2	0,0
15	195,0	3,5	0,0
16	200,0	0,7	0,0

Таблица 2.10

Координаты профиля пятого (периферийного) сечения

Номер точки	x, мм	y в, мм	y н, мм
1	0,0	6,7	6,7
2	2,0	8,6	4,5
3	4,0	9,7	3,7
4	8,0	11,1	2,7
5	16,0	13,2	1,8
6	32,0	15,4	0,9
7	48,0	16,1	0,4
8	56,3	16,09	0,18
9	64,0	16,0	0,0
10	80,0	15,1	0,0
11	96,0	13,3	0,0
12	112,0	11,1	0,0
13	128,0	8,2	0,0
14	144,0	4,9	0,0
15	156,0	1,9	0,0
16	160,0	0,4	0,0

Координаты центра совмещения профилей (ЦСП)

В соответствии с подразд. 1.1 имеем

Для третьего (среднего) сечения

Аналогично для остальных сечений

Углы установки среднего и периферийного сечений

Принимаем для среднего и периферийного сечений углы установки такие же, как были получены по классической методике (см. табл. 2.3), а именно:

φ_ср = 9,4º; φ_периф = 3,9º ≈ 4º.

Определяем координаты одиннадцатой и тринадцатой точек корытца профиля для среднего и периферийного сечений по формулам (1.44) и (1.45).

Для одиннадцатой точки корытца среднего сечения

Для тринадцатой точки корытца среднего сечения

Итак, для среднего сечения имеем две точки:

Для одиннадцатой точки периферийного сечения (см. формулу (1.45))

Для тринадцатой точки корытца периферийного сечения

Итак, для периферийного сечения имеем две точки с номерами одиннадцать и тринадцать:

Рассмотрим пример вычисления координат одиннадцатой и тринадцатой точек для корневого сечения, т. е. для k = 1, а остальные значения координат приведем в виде таблицы.

Выпишем по (1.46) и (1.40) координаты одиннадцатой точки корневого сечения, т. е. k = 1, S_k = – 1,0 (см. табл. 2.7):

Аналогичный расчет произведем для тринадцатой точки корневого сечения:

Итак, для одиннадцатой и тринадцатой точек корневого сечения имеем:

Находим угол установки корневого сечения по формуле (1.43)

,

откуда определяем, что φ₁ = 13°.

Значения координат точек № 11 и 13 корытца промежуточных повернутых профилей и углы установки профилей φ _k приведены соответственно в табл. 2.11 и 2.12.

Таблица 2.11

Координаты точек № 11 и 13 корытца повернутых профилей

Номер сечения	1 (корень)	2	3 (середина)	4	5 (периферия)

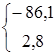
Таблица 2.12

Углы установки профилей

Номер сечения	1 (корень)	2	3 (середина)	4	5 (периферия)
φ k	13°	11,4°	9,4°	7,0°	4,0°

На рис. 2.1 приведены рассчитанные углы установки профилей линейчатой лопасти.

lk, %

Рис. 2.1. Зависимость угла установки профилей линейчатой лопасти
от относительного расстояния сечения лопасти от корневого сечения
для исходных данных примера расчета.