 |
Главная |
Напряжение на отрыв, создаваемое центробежной силой
|
из
5.00
|
Напряжение на отрыв, Н/м2, рассчитываем по формуле
 , ,
| (3.8) |
где S маха — площадь сечения маха в области крепления лопасти (в опасном сечении), м2.
3.7. Момент, создаваемый аэродинамическими силами,
приложенными к лопасти при расчетной скорости ветра
Суммарный момент, создаваемый аэродинамическими силами, действующими на элементарные,
 . .
| (3.9) |
Используя формулу (1.76)  и выражения b ( r ) и r через безразмерные величины получим
и выражения b ( r ) и r через безразмерные величины получим
 . .
| (3.10) |
Интеграл, входящий в правую часть выражения (3.10), можно вычислить по методу трапеций:
 , ,
| (3.11) |
где fi — значение подынтегральной функции на i-м отрезке при замене интеграла суммой.
Величины  , e и b, входящие в правую часть выражения (3.10), определяем соответственно по интерполяционным формулам работы [4], а величина относительной хорды
, e и b, входящие в правую часть выражения (3.10), определяем соответственно по интерполяционным формулам работы [4], а величина относительной хорды  — по выражению (1.19).
— по выражению (1.19).
Если ввести в расчет радиус центра парусности, то момент аэродинамических сил относительно основания лопасти
 , ,
| (3.12) |
где r пар — радиус центра парусности, м; r0 — внутренний радиус ветроколеса, м;
 — —
| (3.13) |
равнодействующая аэродинамических сил, действующих на лопасть, Н; B — коэффициент лобового давления на колесо, о. е.; i лоп — число лопастей.
Коэффициент B, вычисленный для различных величин коэффициента быстроходности Z [4], представлен на графике, приведенном на рис. 3.3.

Рис. 3.3. Зависимость коэффициента лобового давления от
коэффициента быстроходности
По графику на рис. 3.3 определяем, что для Z = 6 … 9 коэффициент лобового давления B = 1,0 … 1,35. Принимаем B = 1,4. Безразмерный радиус центра парусности, выраженный в долях наружного радиуса ветроколеса
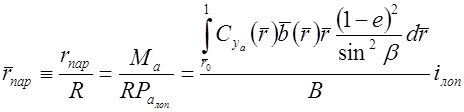 . .
| (3.14) |
Интеграл, стоящий в числителе выражения (3.14), — это тот же интеграл, который входит в соотношение (3.10).
Производя вычисление интеграла по формуле (3.11), можно получить графическую зависимость  , приведенную на рис. 3.4.
, приведенную на рис. 3.4.
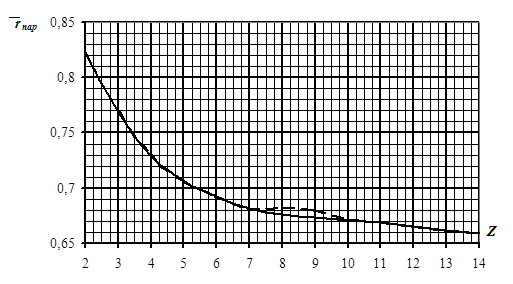
Рис. 3.4. Зависимость безразмерного радиуса центра парусности
от коэффициента быстроходности
Итак, при выбранном значении коэффициента B = 1,4 (с завышением) и величине  , определенной по графику на рис. 3.4 для заданного коэффициента быстроходности Z, получаем момент аэродинамических сил Ma по формуле (3.12), котторая удобна для оценочных расчетов при расчетной скорости ветра.
, определенной по графику на рис. 3.4 для заданного коэффициента быстроходности Z, получаем момент аэродинамических сил Ma по формуле (3.12), котторая удобна для оценочных расчетов при расчетной скорости ветра.
3.8. Сила лобового давления на лопасти ветроколеса
при предельно допустимой скорости ветра
3.8.1. Стабилизируемое ветроколесо
В соответствии с работой [2] для стабилизируемого ветроколеса, сила лобового давления на лопасть при порыве ветра и, в частности, при предельно допустимой скорости ветра
 , ,
| (3.15) |
или
 , ,
| (3.16) |
где V — расчетная скорость ветра, м/с;  — угловая скорость вращения стабилизируемого ветроколеса, с–1; Z — задаваемый коэффициент быстроходности; R — наружный радиус ветроколеса, м; rm — условный радиус лопасти, м;
— угловая скорость вращения стабилизируемого ветроколеса, с–1; Z — задаваемый коэффициент быстроходности; R — наружный радиус ветроколеса, м; rm — условный радиус лопасти, м;
 — —
| (3.17) |
квадрат относительного условного радиуса лопасти;
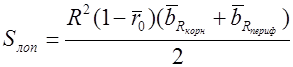 — —
| (3.18) |
площадь лопасти, м2;  — относительный внутренний радиус ветроколеса;
— относительный внутренний радиус ветроколеса;
 — —
| (3.19) |
коэффициент перегрузки при порыве ветра (в нашем случае — при предельно допустимой скорости ветра);
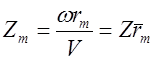 — —
| (3.20) |
условный коэффициент быстроходности при r = rm;
 — —
| (3.21) |
коэффициент порыва;
V пред.доп — предельно допустимая скорость ветра, м/с.
3.8.2. Нестабилизируемое ветроколесо
В случае нестабилизируемого ветроколеса сила лобового давления на лопасть при предельно допустимой скорости ветра по [1] имеет вид:
 , ,
| (3.22) |
где 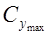 , r и S лоп — те же величины, что и для стабилизируемого ветроколеса;
, r и S лоп — те же величины, что и для стабилизируемого ветроколеса;
 — —
| (3.23) |
квадрат условного радиуса лопасти; 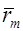 — относительный условный радиус лопасти, о. е.;
— относительный условный радиус лопасти, о. е.;
 — —
| (3.24) |
угловая скорость при предельно допустимой скорости ветра для нестабилизируемого ветроколеса, с–1.
Учитывая формулы (3.23) для rm и (3.24) для 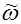 , имеем для Pmax в случае нестабилизируемого ветроколеса
, имеем для Pmax в случае нестабилизируемого ветроколеса
 , ,
| (3.25) |
где Z — задаваемый коэффициент быстроходности.
3.9. Изгибающий момент, создаваемый силой лобового давления
на лопасть при предельно допустимой скорости ветра
Стабилизируемое ветроколесо
Изгибающий момент от силы лобового давления на лопасть при предельно допустимой скорости ветра
 , ,
| (3.26а) |
где  — вычисляется по формуле (3.15);
— вычисляется по формуле (3.15); 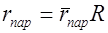 ,
, 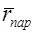 — относительный (в долях радиуса ветроколеса) радиус парусности лопасти, величина
— относительный (в долях радиуса ветроколеса) радиус парусности лопасти, величина 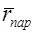 определяется по графику на рис. 3.4 для заданного коэффициента быстроходности;
определяется по графику на рис. 3.4 для заданного коэффициента быстроходности; 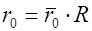 — внутренний радиус ветроколеса;
— внутренний радиус ветроколеса; 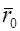 — задаваемая величина относительного внутреннего радиуса ветроколеса — обычно принимается
— задаваемая величина относительного внутреннего радиуса ветроколеса — обычно принимается  .
.
Нестабилизируемое ветроколесо
Изгибающий момент от силы лобового давления на лопасть при предельно допустимой скорости ветра для нестабилизируемого ветроколеса
 , ,
| (3.26б) |
где Pmax — вычисляется по формуле (3.25); r пар и r0 — вычисляются так же, как и в случае стабилизируемого ветроколеса.
3.10. Момент, создаваемый распределенными центробежными силами,
действующими на лопасть
В соответствии с [1], момент, создаваемый распределенными центробежными силами, действующими на лопасть, и стремящийся повернуть лопасть перпендикулярно валу ветроколеса, равен
 , ,
| (3.27) |
где w — угловая частота вращения ветроколеса, с-1; j — угол заклинения (установки) профиля в корневом сечении, градус;
 , — , —
| (3.28) |
момент инерции лопасти относительно ее оси; r ц — полярный радиус произвольной точки профиля.
В случае лопасти постоянной плотности r лоп
 . .
| (3.29) |
В цилиндрических координатах
 .
.
Считая профили одинаковыми по высоте лопасти и совпадающими с корневым профилем (для того, чтобы создать запас прочности) получаем
 , ,
| (3.30) |
где l — длина лопасти.
Произведя интегрирование по r ц, имеем
 . .
| (3.31) |
Точечную зависимость 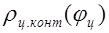 можно получить, пользуясь
можно получить, пользуясь
рис. 3.2 и табл. 3.1.
Вначале найдем абсциссы точек контура в системе координат X ц0ц Y ц:
 , ,
| (3.32) |
 . .
| (3.33) |
В случае профиля типа «Эсперо»
x ц.т = 0,352b, y ц.т = 0,4c .
Построим цепочку координат точек всего контура профиля при его обходе против часовой стрелки: 0 £ j ц £ 2p (рис. 3.5). Количество то-
чек — 2n + 1. В случае нашего примера при n = 11 — всего 23 точки. Примем номер промежуточной точки k, где k меняется от 1 до 23. Пусть начало отсчета (k = 1), соответствует j ц = 0, тогда последняя точка, k = 23, будет соответствовать j ц = 2p.

Рис. 3.5. Построение цепочки точек при обходе контура профиля
Для k = 1, 2, …, 7
 . .
| (3.34) |
для k = 8, 9, …, 18
 . .
| (3.35) |
для k = 19, 20, …, 23
 . .
| (3.36) |
Выражая y ц через  , находим соотношение
, находим соотношение
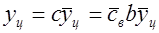 ,
,
которое получается из формул (3.34) — (3.36).
Для  получаем следующие соотношения:
получаем следующие соотношения:
- для k = 1, 2, …, 7
 ; ;
| (3.37) |
- для k = 8, 9, …, 18
 ; ;
| (3.38) |
- для k = 19, 20, …, 23
 . .
| (3.39) |
Безразмерные в долях хорды b абсциссы точек, соответствующих номерам k = 1, 2, …, 23 при круговом обходе профиля (см. рис. 3.5) в системе координат X ц O ц Y ц, представим в табл. 3.2.
Таблица 3.2
Безразмерные абсциссы точек при круговом обходе профиля
в долях хорды b
| Номер точки | 
| Номер точки | 
| Номер точки | 
| Номер точки | 
|
| 1 | 0,503 | 7 | 0,048 | 13 | -0,346 | 19 | 0,648 |
| 2 | 0,453 | 8 | -0,085 | 14 | -0,351 | 20 | 0,628 |
| 3 | 0,404 | 9 | -0,202 | 15 | -0,342 | 21 | 0,590 |
| 4 | 0,344 | 10 | -0,262 | 16 | -0,319 | 22 | 0,551 |
| 5 | 0,276 | 11 | -0,300 | 17 | -0,238 | 23 | 0,503 |
| 6 | 0,194 | 12 | -0,329 | 18 | 0,048 |
Отметим, что 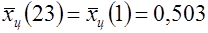 .
.
Определим полярные углы j ц каждой их 23-х точек.

| (3.40) |
где  для k = 1, 2, 3, …, 23 изменяется в соответствии с
для k = 1, 2, 3, …, 23 изменяется в соответствии с
табл. 3.2, а y ц для k = 1, 2, 3, …, 23 — в соответствии с формулами
(3.34) — (3.36).
Величины y ц и x ц, входящие в отношение y ц/x ц, можно выразить через 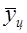 и
и  :
:

| (3.41) |
Полярный радиус точки контура профиля
 . .
| (3.42) |
Подставив ρц.конт из выражения (3.38) в формулу (3.27), получим
 . .
| (3.43) |
Определим приближенное значение интеграла, входящего в соотношение (3.43) для момента инерции, по методу трапеций с переменным шагом:
 , ,
| (3.44) |
где f(φц), fk и hk рассчитываем по формулам (3.33) — (3.34):
|
| (3.45) | |
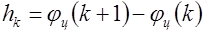 — —
| (3.46) | |
переменный шаг при численном интегрировании.
Обозначим через Ss комплекс, зависящий от  и входящий в (3.43):
и входящий в (3.43):
 . .
| (3.47) |
Для профиля пятнадцатипроцентной толщины (  )
)
Ss(0,15) ≈ 0,0998.
Значения комплекса Ss для других значений  даны в табл. 3.3. В этой же таблице приведены значения коэффициента Kc учета относительной толщины профиля при вычислении момента инерции профиля,
даны в табл. 3.3. В этой же таблице приведены значения коэффициента Kc учета относительной толщины профиля при вычислении момента инерции профиля,
 .
.
Таблица 3.3
Учет влияния толщины профиля на комплекс Ss

| 0,10 | 0,12 | 0,15 | 0,18 | 0,20 | 0,22 | 0,24 | 0,26 |
| Ss | 0,0756 | 0,0857 | 0,0998 | 0,1100 | 0,1170 | 0,1235 | 0,1300 | 0,1360 |
| Kc | 0,756 | 0,867 | 1,0 | 1,116 | 1,193 | 0,270 | 0,347 | 1,424 |
Аппроксимация в виде ломаной величин Kc при различных величинах  , представленных в табл. 3.3, дает следующие формулы:
, представленных в табл. 3.3, дает следующие формулы:
- для 
 ; ;
| (3.48) |
- для 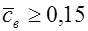
 . .
| (3.49) |
Итак,
 , ,
| (3.50) |
где
| Ss = 0,0988K с, | (3.51) |
а коэффициент K с определяем по формулам (3.48) и (3.49).
Для профиля пятнадцатипроцентной толщины
K с = 1, Ss = 0,0988.
Итак, момент инерции сплошной лопасти рассчитан.
|
из
5.00
|
Обсуждение в статье: Напряжение на отрыв, создаваемое центробежной силой |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


 ;
;