 |
Главная |
Частные случаи приведения пространственной системы сил
|
из
5.00
|
Системы сил
Изменение главного момента при перемене центра приведения
Согласно теореме Пуансо, произвольная система сил приводится к главному вектору 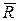 и главному моменту
и главному моменту 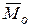 (
( 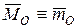 ) относительно произвольного центра приведения
) относительно произвольного центра приведения 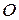 (рис. 9.1):
(рис. 9.1):
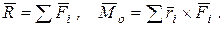 (9.1)
(9.1)
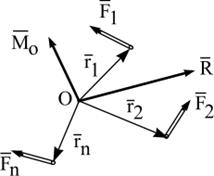
| Здесь При перемене центра приведения векторные моменты сил изменяются, так как изменяются радиус-векторы точек приложения (рис. 9.2). |
| Рис. 9.1 | |
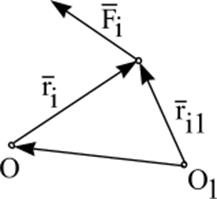
| Вследствие этого изменяется главный момент. Оценим изменение главного момента заданной системы сил. Из рис. 9.2 видно, что
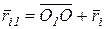 ,
где ,
где 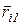 - радиус - вектор точки приложения силы - радиус - вектор точки приложения силы 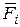 , проведенный из центра , проведенный из центра 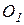 . .
|
| Рис. 9.2 |
Тогда главный момент системы 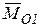 относительно нового центра приведения запишется
относительно нового центра приведения запишется
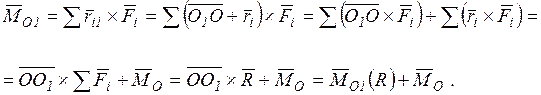
Здесь 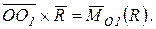
| Получили, что главный момент относительно нового центра приведения (точка О1) (рис. 9.3) является векторной суммой моментов
| 
|
| Рис.9.3 |
Итак, главный момент системы сил при перемене центра приведения изменяется на векторный момент главного вектора 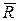 , приложенного в старом центре приведения относительно нового центра приведения О1.
, приложенного в старом центре приведения относительно нового центра приведения О1.
9.2. Инварианты системы сил
Физические величины инвариантны относительно данного преобразования координат, если значения этих величин не меняются при переходе к другой системе координат.
Главный вектор для любого центра приведения выражается векторной суммой: 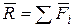 . Таким образом, главный вектор системы сил является векторным инвариантом. Для одной и той же системы сил он не зависит от выбора центра приведения.
. Таким образом, главный вектор системы сил является векторным инвариантом. Для одной и той же системы сил он не зависит от выбора центра приведения.
Получим второй скалярный инвариант. Для этого умножим правую и левую части уравнения (9.2) скалярно на 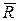 , получим
, получим
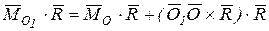 , (9.3)
, (9.3)
или
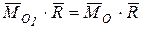 , (9.4)
, (9.4)
так как смешанное произведение векторов, содержащих два одинаковых множителя R, равно нулю, т.е. 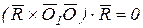 .
.
Как видно из соотношения (9.4), скалярное произведение главного момента на главный вектор не зависит от центра приведения, т.е. является вторым скалярным инвариантом: Выражение (9.4) можно записать так:
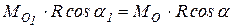 ,
,
где 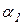 - угол между векторами
- угол между векторами 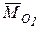 и
и 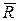 , а
, а 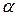 - между
- между 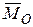 и
и 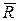 (рис. 9.4). После сокращения на R получим
(рис. 9.4). После сокращения на R получим
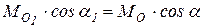 . (9.5)
. (9.5)
| Проекция главного момента на направление главного вектора не зависит от центра приведения. Разложим главный момент в каждом центре приведения на две взаимно перпендикулярные | 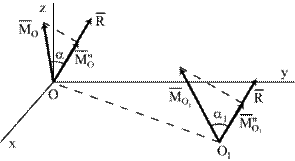
|
| Рис.9.4 |
составляющие, одна из которых направлена по главному вектору 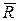 . Учитывая, что главные векторы в различных центрах приведения согласно (9.5) равны, получим (рис.9.4):
. Учитывая, что главные векторы в различных центрах приведения согласно (9.5) равны, получим (рис.9.4):
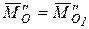 .
.
Частные случаи приведения пространственной системы сил
Произвольная система сил приводится к силе, равной главному вектору 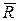 и паре сил, векторный момент которой равен главному моменту
и паре сил, векторный момент которой равен главному моменту 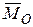 . В зависимости от их взаимного направления, т.е. угла
. В зависимости от их взаимного направления, т.е. угла 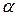 между ними, можно произвести дальнейшие упрощения.
между ними, можно произвести дальнейшие упрощения.
Приведение к паре сил. Если 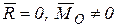 , то система сил приводится к одной паре сил, причем главный момент в этом случае, согласно (9.5), не зависит от выбора центра приведения. В этом случае оба инварианта системы равны нулю, т.е.
, то система сил приводится к одной паре сил, причем главный момент в этом случае, согласно (9.5), не зависит от выбора центра приведения. В этом случае оба инварианта системы равны нулю, т.е. 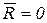 ,
, 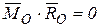 .
.
Приведение к равнодействующей. Возможны два случая.
Если 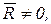
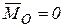 (первый инвариант
(первый инвариант 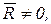 второй -
второй - 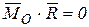 ), то система приводится к равнодействующей силе
), то система приводится к равнодействующей силе 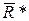 , равной по модулю и направлению главному вектору
, равной по модулю и направлению главному вектору 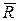 , т.е.
, т.е. 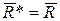 . Линия действия равнодействующей силы в этом случае проходит через центр приведения.
. Линия действия равнодействующей силы в этом случае проходит через центр приведения.
Если 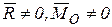 , но α=90˚, т.е.
, но α=90˚, т.е. 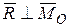 (первый инвариант
(первый инвариант 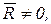 второй
второй 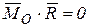 ), то система сил тоже приводится к равнодействующей, причем опять
), то система сил тоже приводится к равнодействующей, причем опять 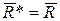 . Но линия действия равнодействующей силы
. Но линия действия равнодействующей силы 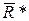 находится на расстоянии от центра приведения на расстоянии
находится на расстоянии от центра приведения на расстоянии 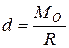 (рис.9.5).
(рис.9.5).
В этом случае имеем силу 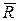 и пару сил с векторным моментом
и пару сил с векторным моментом 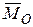 , причем силы пары можно считать расположенными в одной плоскости с равнодействующей
, причем силы пары можно считать расположенными в одной плоскости с равнодействующей 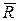 , так как векторный момент пары перпендикулярен
, так как векторный момент пары перпендикулярен 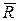 .
.
Поворачивая и перемещая пару сил в ее плоскости, а также изменяя силу пары и ее плечо, при сохранении модуля векторного момента, можно получить одну из сил пары 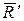 , равной по модулю, но противоположной по направлению главному вектору
, равной по модулю, но противоположной по направлению главному вектору  .
.
| Другая сила пары
Отрезок d определяет кратчайшее расстояние |
| Рис.9.5 |
от центра приведения О до линии действия  .
.
Приведение к динаме.
Совокупность силы и пары сил, лежащей в плоскости, перпендикулярной силе, носит название динама или динамического вектора (рис. 9.а).
| а | 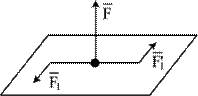
| б | 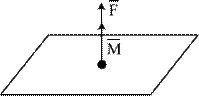
|
| Рис.9.6 | |||
Используя векторный момент 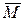 пары
пары 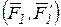 , можно также определить динаму как совокупность силы и пары сил, в которой сила параллельна векторному моменту пары сил (рис.9.6б). Сила
, можно также определить динаму как совокупность силы и пары сил, в которой сила параллельна векторному моменту пары сил (рис.9.6б). Сила 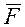 и векторный момент пары
и векторный момент пары
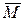 могут быть направлены как в одну, так и в противоположные стороны.
могут быть направлены как в одну, так и в противоположные стороны.
Рассмотрим случай, в котором главный вектор 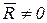 , главный момент относительно центра О
, главный момент относительно центра О 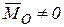 и векторы
и векторы 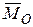 и
и 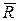 неперпендикулярные. В этом случае оба инварианта не равны нулю, т.е.
неперпендикулярные. В этом случае оба инварианта не равны нулю, т.е. 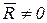 ,
, 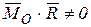 .
.
Если центр приведения О выбран произвольно (рис. 9.7), то главный вектор 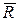 и главный момент
и главный момент  будут составлять между собой некоторый угол
будут составлять между собой некоторый угол  , в общем случае отличный от нуля.
, в общем случае отличный от нуля.
Рис. 9.7
Разложим главный момент 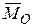 на две составляющие: составляющую
на две составляющие: составляющую 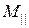 , направленную вдоль главного вектора
, направленную вдоль главного вектора 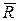 , и составляющую
, и составляющую 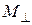 , перпендикулярную к главному вектору - таким образом, что
, перпендикулярную к главному вектору - таким образом, что
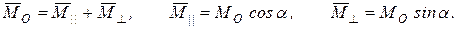
Вектор 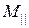 как инвариант системы, согласно (9.5), есть величина для данной системы постоянная, не зависящая от выбора центра приведения. Причем численно из (9.4) получим
как инвариант системы, согласно (9.5), есть величина для данной системы постоянная, не зависящая от выбора центра приведения. Причем численно из (9.4) получим
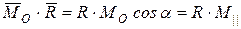 ,
,
откуда 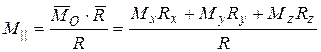 .
.
Таким образом, с изменением центра приведения будет изменяться только перпендикулярная составляющая 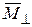 . Мы всегда можем найти такой центр приведения
. Мы всегда можем найти такой центр приведения 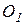 , чтобы составляющая
, чтобы составляющая 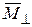 обращалась в нуль; тогда главный момент и главный вектор будут направлены по одной прямой, т.е. будут коллинеарные, а вектор главного момента будет иметь минимальную величину, равную
обращалась в нуль; тогда главный момент и главный вектор будут направлены по одной прямой, т.е. будут коллинеарные, а вектор главного момента будет иметь минимальную величину, равную 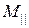 .
.
Линия, вдоль которой направлена сила динамы 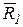 , называется центральной винтовой осью. Во всех точках винтовой оси, принятых за центры приведения, система приводится к одной и той же динаме. Расстояние от центра приведения О до центральной винтовой оси
, называется центральной винтовой осью. Во всех точках винтовой оси, принятых за центры приведения, система приводится к одной и той же динаме. Расстояние от центра приведения О до центральной винтовой оси
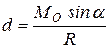 .
.
| Совокупность сил, образующих динаму, можно заменить двумя скрещивающимися силами. Для этого следует одну из сил пары | а | 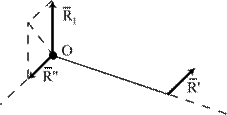
|
| б | 
| |
| Рис.9.8 | ||
|
из
5.00
|
Обсуждение в статье: Частные случаи приведения пространственной системы сил |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


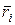 - радиус - вектор точки приложения силы
- радиус - вектор точки приложения силы 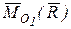 , т.е.
, т.е.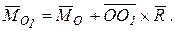 (9.2)
(9.2) , которая по модулю и направлению совпадает с главным вектором
, которая по модулю и направлению совпадает с главным вектором  определяется из условия
определяется из условия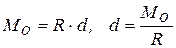 .
.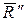 (рис.9.8а) совместить с точкой приложения силы
(рис.9.8а) совместить с точкой приложения силы 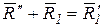 ). Итак, рассмотрены все возможные случаи, кроме случая равновесия системы сил (
). Итак, рассмотрены все возможные случаи, кроме случая равновесия системы сил ( 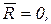
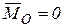 ), рассмотренного ранее в лекции 6.
), рассмотренного ранее в лекции 6.