Решения задач муниципального этапа всероссийской олимпиады школьников по математике 2017 год

Решения задач муниципального этапа всероссийской олимпиады школьников по математике 2017 год

Класс

Задача 1. Красная Шапочка решила сходить к бабушке, домик которой находился в 1 км ходьбы от ее дома. Волк ей в тот день не попался, поэтому туда и обратно она шла по одному и тому же маршруту. На горизонтальных участках ее скорость была 4 км/ч, в гору – 3 км/ч, а с горы – 6 км/ч. Сколько времени она была в пути?

Ответ. Полчаса.

Решение. Рассмотрим какой-нибудь наклонный участок пути длиной s. Проходя его в гору, Красная Шапочка потратит время s/3, под гору – s/6, всего -- . Значит, ее средняя скорость на этом участке составляет . Итак, средняя скорость на всех участках одинакова и равна  км/ч. Весь путь девочки составляет 2 км, так что она потратит на дорогу полчаса.

Критерии. За ответ без обоснования – 0 баллов, за решение на отдельных примерах – 1 балл. За полное обоснование 7 баллов.

 

Задача 2. Петя утверждает, что два спинера дороже пяти мороженых, Вася -- что три спинера дороже восьми мороженых. Известно, что прав из них только один. Верно ли, что 7 спинеров дороже 19 мороженых?

Ответ. Неверно.

Решение. Обозначим цену спинера через s, а мороженого – через m. Первое утверждение означает, что , второе – что . Если бы выполнялось второе условие, то выполнялось бы и первое, что противоречит условию. Значит, . Но тогда .

Критерии. За ответ без обоснования – 0 баллов, за решение на отдельных примерах – 0 баллов. За полное обоснование 7 баллов.

 

Задача 3. В выпуклом четырёхугольнике длины диагоналей 2 и 4 см. Найти площадь четырёхугольника, зная, что длины отрезков, соединяющих середины противоположных сторон, равны.

D

A

C

B

P

Q

R

T

Ответ. 4 см2.

Решение. Отрезок, соединяющий середины смежных сторон четырехугольника параллелен его диагонали (как средняя линия соответствующего треугольника). Поэтому четырехугольник PQRT – параллелограмм. По условию диагонали этого параллелограмма равны, так что он является прямоугольником. Но тогда и диагонали AC и BD, параллельные его сторонам, перпендикулярны между собой.

O

A

C

B

D

N

M

K

L

Проведем через вершины прямоугольника прямые, параллельные диагоналям. Получим описанный прямоугольник KLMN. Заметим, что треугольник AMD равен ADO, CDN – треугольнику CDO и т.д. Поэтому площадь KLMN вдвое больше, чем площадь ABCD. Итак, искомая площадь составляет S = ½ ž2ž4 = 4.

Замечание. Возможны и другие способы вычисления S, например, как удвоенной площади PQRT. Также можно использовать формулу S = ½ ACžBDžsin a, где a – угол между диагоналями.

Критерии. За разбор частного случая – 0 баллов. Доказательство того, что SPQR – прямоугольник – 3 балла.

Задача 4. Три прямые, пересекаясь, образуют 12 углов, причем n из них оказались равными. Каково может быть максимальное значение n?

Ответ. 6.

Решение. Три прямые ограничивают некий треугольник. Если этот треугольник равносторонний, то из двенадцати углов шесть составляют 60°, а остальные шесть -- 120°.

Может ли какой-нибудь внешний угол треугольника быть равным его внутреннему углу? Он равен сумме несмежных с ним внутренних, так что он больше каждого из несмежных. Значит, равным он может быть только смежному с ним. Тогда каждый из них составляет 90°, таких углов 4 (у них общая вершина). Других прямых углов в этой конструкции нет. Но тогда другие внешние углы не равны внутренним. Равными могут быть только внутренние (и вертикальные к ним) или только внешние (и вертикальные к ним). Тогда равных углов каждого типа будет не более 4.

Критерии. За пример с шестью равными углами – 3 балла, за сравнение внешних и внутренних углов – 3 балла. За ответ без обоснования – 1 балл.

 

 

Задача 5. Рассмотрим четыре последовательных числа n, n + 1, n + 2, n + 3. Для каких n НОК первых трех чисел больше, чем НОК последних трех?

Ответ. Любое нечетное число не меньшее 5.

Решение. Рассмотрим тройку чисел n, n + 1, n + 2. Каждые два соседних числа взаимно просты. Если числа n и n + 2 имеют общий делитель, то он является делителем их разности, 2. Итак, если число n нечетное, то все три числа n, n + 1, n + 2 попарно взаимно просты, так что НОК(n, n + 1, n + 2) = n(n + 1)(n + 2). Если n четное, то НОК(n, n + 1, n + 2) = n(n + 1)(n + 2)/2. Ясно, НОК(n + 1, n + 2, n + 3)  может быть меньше НОК(n, n + 1, n + 2), только если n – нечетное. Неравенство принимает вид

или после сокращения 2n > n + 3. Окончательно n > 3, откуда в силу нечетности n ³ 5.

Критерии. За вычисление НОК для случая нечетных n – 2 балла, для случая четных -- 3 балла. За полное решение – 7 баллов. За отдельные примеры – 0 баллов.

 

Решения задач муниципального этапа всероссийской олимпиады школьников по математике 2017 год

Класс

Задача 1. При каких p один из корней уравнения x2 + px + 18 = 0 вдвое больше другого?

Ответ. 9 или –9.

Решение. Пусть корни уравнения есть a и 2a. По теореме Виета a + 2a = –p, až2a = 18. Значит, a = ±3, p = –3a.

Критерии. За потерю второго решения – вычитаются 2 балла. За ответ без обоснования – 0 баллов. Допускается решение без использования теоремы Виета. В случае полного обоснования – оценка 7 баллов.

 

 

2. Известно, что число a = рационально. Доказать, что число b = 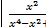 также рационально.

Решение. При x = 0 число b = 0 – рационально. Если x ¹ 0, то и a ¹ 0, b ¹ 0. Тогда  можно записать , . Значит, . Возведем это равенство в квадрат, получим 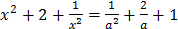, откуда , то есть b = . В силу рациональности a эта дробь также рациональна. Осталось только проверить, что b всегда существует. Знаменатель мог бы обратиться в ноль при , что невозможно в силу рациональности a.

Критерии. Если не исследован случай x = 0, снимается 1 балл. Если не проверено, что b существует – снимается 3 балла. В случае полного обоснования – оценка 7 баллов.

 

 

3. Натуральное число n таково, что числа 2n + 1 и 3n + 1 являются квадратами. Может ли при этом число n быть простым?

Ответ. Нет, не может.

Решение. Пусть 2n + 1 = a² и 3n + 1 = b², тогда

n = (3n + 1) – (2n + 1) = b² – a² = (b-a)(b+a).

Если число n — простое, то b – a = 1 и b + a = n. Из этих равенств легко выразить числа a и b через n: a =  и b = 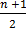. Подставив выражение для aв исходное равенство 2n + 1 = a², получим квадратное уравнение n² – 10n – 3 = 0, которое не имеет целых корней. Значит, такого простого числа n нет.

Критерии. Доказано только равенствоn = (b-a)(b+a) — 2 балла.

 

E

A

B

C

D

F

4. Угол при вершине B равнобедренного треугольника ABC равен 108°. Докажите, что биссектриса угла A вдвое больше биссектрисы угла B.

Решение. Пусть AD и BE — биссектрисы равнобедренного треугольника ABC. Через точку E проведём отрезок EF параллельно AD, тогда EF – средняя линия треугольника ACD, и EF = AD. Несложным подсчётом углов получаем ∠FBE = ∠BFE = 54◦, и значит, треугольник BEF — равнобедренный. Отсюда BE = EF = AD, и поэтому AD = 2·BE.

Критерии. В случае полного обоснования – оценка 7 баллов.

 

 

5. а) Какое наибольшее количество неперекрывающихся полосок 1 × 3 можно уместить на салфетке, изображенной на рисунке? б) Какое наименьшее количество полосок 1 × 3 потребуется, чтобы покрыть салфетку целиком, если полоски могут перекрываться?

Рис. 1, а

Рис. 1, б

Рис. 2, а

Рис. 2, б

Ответ.

Решение. а) Раскрасим клетки на салфетке, как показано на рисунке 1,а («диагональная» рас-краска). Каждая полоска 1×3 не может содержать более одной чёрной клетки. Поскольку чёрных кле-ток всего 7, мы не можем уместить на салфетке более 7 полосок (оценка). На рисунке 1,б приведён пример 7 полосок, которые можно разместить на салфетке.

б) Раскрасим клетки на салфетке, как показано на рисунке 2,а. Каждая полоска 1×3 не может со-держать более одной чёрной клетки. Поскольку чёрных клеток всего 11, для покрытия салфетки по-надобится не менее 11 полосок (оценка). На рисун-ке 2,б приведен пример 11 полосок, которые целиком покрывают салфетку.

Критерии. Ответ без обоснования – по 1 баллу за каждый пункт. Доказано, что число наибольшее или наименьшее – по 3 балла за каждый пункт. Полное решение – 7 баллов.