Решения задач муниципального этапа всероссийской олимпиады школьников по математике 2017 год

Класс

1. Известно, что sin(a + b) = 0,2 и cos(a − b) = 0,3. Вычислите sin(α + 45°)žsin(β + 45°).

Ответ. 0,25.

Решение. По формуле для синуса суммы углов имеем

sin(j + 45°) = (sin j + cos j),

и значит, P = sin(a + 45°) × sin(b + 45°) = (sin a + cos a)(sin b + cos b). Раскрывая скобки и вновь используя формулу для синуса и косинуса суммы углов, получим

P = (sin (a + b) + cos (a – b)) = 0,25.

Критерии. Доказано равенство P = (sin a + cos a)(sin b + cos b) — 1 балл.

 

2. При каких q один из корней уравнения x2 – 12x + q = 0 является квадратом другого?

Ответ. –64 или 27.

Решение. Пусть корни уравнения есть a и a2. По теореме Виета a + a2 = 12, aža2 = q. Значит, a = –4 или a = 3, q = a3.

Критерии. Только ответ – 1 балл. В случае полного обоснования – оценка 7 баллов.

 

 

3. Пусть x1, x2, … , x100 — некоторые числа, принадлежащие отрезку [0; 1]. Верно ли, что на этом отрезке найдётся такое число x, что |x − x1| + |x − x2| + . . . + |x − x100| = 50?

Ответ. Верно.

Решение. Рассмотрим функцию f(x) = |x − x1| + |x − x2| + ... + |x − x100| − 50, непрерывную на отрезке [0;1]. Имеем f(0) = x1 + x2 + … + x100 – 50, f(1) = (1 – x1) + (1 – x2) + … + (1 – x100) – 50. Значит, f(0) + f(1) = Sxi + S(1 − xi) − 100 = 0.

Если числа f(0) и f(1) равны 0, то уравнение имеет, по крайней мере, два корня: 0 и 1. Если же одно из этих чисел отрицательное, то другое — положительное. Поскольку f — непрерывная функция, существует такое x ∈ [0;1], при котором f(x) = 0.

Критерии. В случае полного обоснования – оценка 7 баллов.

 

 

4. Две окружности, радиусы которых относятся как 2 : 3, касаются внутренним образом. Через центр меньшей окружности проведена прямая, перпендикулярная линии центров, из точек пересечения этой прямой с большей окружностью проведены касательные к меньшей окружности. Найти углы между этими касательными.

Ответ. Все углы прямые.

O1

O2

B

A

2

3

1

M

N

Решение. По теореме Пифагора O2B = . Из прямоугольного треугольника O2BM находим BM = 2. Значит, треугольник O2BM равнобедренный, с углом 45°. Аналогично и угол O2BN составляет 45°.

Итак, касательные, проведенные из одной точки к меньшей окружности перпендикулярны между собой.

Можно проводить расчет и другими способами.

Критерии. В случае полного обоснования – оценка 7 баллов.

 

 

5. а) Какое наибольшее количество неперекрывающихся полосок 1 × 3 можно уместить на салфетке, изображенной на рисунке? б) Какое наименьшее количество полосок 1 × 3 потребуется, чтобы покрыть салфетку целиком, если полоски могут перекрываться?

Рис. 1, а

Рис. 1, б

Рис. 2, а

Рис. 2, б

Ответ.

Решение. а) Раскрасим клетки на салфетке, как показано на рисунке 1,а («диагональная» рас-краска). Каждая полоска 1×3 не может содержать более одной чёрной клетки. Поскольку чёрных кле-ток всего 7, мы не можем уместить на салфетке более 7 полосок (оценка). На рисунке 1,б приведён пример 7 полосок, которые можно разместить на салфетке.

б) Раскрасим клетки на салфетке, как показано на рисунке 2,а. Каждая полоска 1×3 не может со-держать более одной чёрной клетки. Поскольку чёрных клеток всего 11, для покрытия салфетки по-надобится не менее 11 полосок (оценка). На рисун-ке 2,б приведен пример 11 полосок, которые целиком покрывают салфетку.

Критерии. Ответ без обоснования – по 1 баллу за каждый пункт. Доказано, что число наибольшее или наименьшее – по 3 балла за каждый пункт. Полное решение – 7 баллов.

 

Решения задач муниципального этапа всероссийской олимпиады школьников по математике 2017 год

Класс

1. При каких p один из корней уравнения x2 – px + p = 0 является квадратом другого? (считаем, что корни уравнения различны)

Ответ. .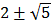

Решение. Обозначим корни a и a2. По теореме Виета a + a2 = p, aža2 = p. Значит, a + a2 = a3. Корень a = 0 не подходит, так как у уравнения x2 = 0 корни совпадают. С учетом a ¹ 0 получаем, что a2 – a – 1 = 0, корнями этого уравнения являются . При этом p = a2 + a = (a + 1) + a = 2a + 1.

Критерии. Если не отброшен лишний корень, снимается 2 балла. В случае полного обоснования – оценка 7 баллов.

 

 

2. Петя нашёл сумму всех нечётных делителей некоторого чётного натурального числа n, а Вася – сумму всех его чётных делителей. Может ли произведение их результатов оказаться равным 2016? Если может, найдите все такие числа n.

Ответ. 88 и 192.

Решение. Пусть n = m·2k – исходное чётное число, и m – его нечётный множитель. Сумма нечётных делителей числа n совпадает с суммой s всех делителей числа m, и значит, Петя получит число s. Сумма всех чётных делителей n состоит из суммы делителей, которые делятся только на 2, из суммы делителей, кратных только 4, и так далее, и наконец, из суммы делителей, кратных 2k. Каждый нечётный делитель при умножении на 2 – это делитель, кратный только 2, поэтому первая сумма равна 2s, вторая сумма – 4s и так далее. Следовательно, сумма всех чётных делителей будет 2s + 4s + ... + 2ks = 2(2k − 1)s. Произведение результатов Пети и Васи равно 2s2(2k − 1) = 2016, и, значит, s2(2k − 1) = 1008.

Полученное равенство означает, что число 1008 = 24·32·7 делится на квадрат натурального числа s > 1 и число вида 2k − 1. Среди разложений числа 1008 = 22·252 = 32·112 = 42·63 = 62·28 = 122·7, содержащих квадрат натурального числа, сомножитель вида 2k − 1 содержат только разложения 42·63 и 122·7. Значит, s = 4, k = 6, или s = 12, k = 3. В первом случае, m = 3, и значит, n = 3·26 = 192; во втором – m = 11, и значит, n = 11·23 = 88.

Критерии. В случае полного обоснования – оценка 7 баллов.

 

 

3. В прямоугольном параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ стороны AB = 2, AC = 3, AA ₁ = 4. Найти площадь сечения AMK , где M – середина BB ₁ и K – середина DD ₁ .

Ответ. 2

A

B

C

D

A1

B1

C1

D1

2

3

4

M

K

P

Q

Решение. Построим искомое сечение (см. рисунок). Точка P есть пересечение AM и A ₁ B ₁, В силу положения точки M A ₁ P вдвое больше, чем A ₁ B ₁. Аналогично строим точку Q, A ₁ Q = 2A ₁ D ₁. Значит, PQ параллельно B ₁ D ₁ и проходит через точку C ₁. Итак, сечение является параллелограммом AKC ₁ M.

Площадь можно вычислить разными способами.

1 способ. Заметим, что KM = BD = AC = 3, AM = , AD = , AK = . Итак, треугольник AKM равнобедренный, его высота равна . Тогда площадь сечения составляет 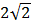ž  = 2 .

2 способ. Используем векторы. Известно, что S = , в то время как 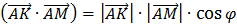 значит, . Заметим, что с параллелепипедом можно связать систему координат с началом с точке A. Имеем  и . Тогда , ,  = 0 + 0 + 4 = 4 откуда и следует ответ.

Замечание. Возможны и другие способы вычисления площади. Например, через векторное произведение векторов  и .

Критерии. В случае полного обоснования – оценка 7 баллов.

 

4. Пусть x1, x2, … , x100 — некоторые числа, принадлежащие отрезку [0; 1]. Верно ли, что на этом отрезке найдётся такое число x, что |x − x1| + |x − x2| + . . . + |x − x100| = 50?

Ответ. Верно.

Решение. Рассмотрим функцию f(x) = |x − x1| + |x − x2| + ... + |x − x100| − 50, непрерывную на отрезке [0;1]. Имеем f(0) = x1 + x2 + … + x100 – 50, f(1) = (1 – x1) + (1 – x2) + … + (1 – x100) – 50. Значит, f(0) + f(1) = Sxi + S(1 − xi) − 100 = 0.

Если числа f(0) и f(1) равны 0, то уравнение имеет, по крайней мере, два корня: 0 и 1. Если же одно из этих чисел отрицательное, то другое — положительное. Поскольку f — непрерывная функция, существует такое x ∈ [0;1], при котором f(x) = 0.

Критерии. В случае полного обоснования – оценка 7 баллов.

 

 

5. На доске размером 10×10 стоят 10 небьющих друг друга ладей. Можно ли остальные клетки доски замостить доминошками? (Доминошка — прямоугольник размером 1×2 или 2×1.

Ответ. Нельзя.

Решение. Для каждой ладьи с номером i обозначим через si сумму номеров строки и столбца, в которых она стоит. Поскольку ладьи не бьют друг друга, то номера всех строк и столбцов встречаются ровно по одному разу. Сумма всех чисел si независимо от расстановки будет чётной и равна

 Из этого равенства, в частности, следует, что количество нечётных чисел si будет чётным. Таким образом, из 10 чисел si количества нечётных и чётных значений не совпадают. Предположим, левый нижний угол доски покрашен в чёрный цвет, тогда у всех чёрных клеток доски числа si чётные, а у белых клеток – нечётные. Поскольку количества нечётных и чётных значений si не совпадают, ладей на чёрных и белых клетках – разное количество. Значит, разными будут и количества белых и чёрных свободных от ладей клеток. Так как каждая доминошка закрывает по одной чёрной и белой клетке доски, то оставшиеся свободные клетки выложить доминошками не удастся.

Критерии. В случае полного обоснования – оценка 7 баллов.