 |
Главная |
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
|
из
5.00
|
Задача 198. Доказать, что 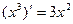 .
.
Решение. По определению, 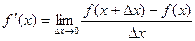 =
= 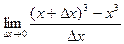 =
= 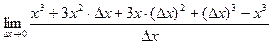 =
=
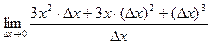 =
= 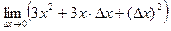 =
= 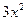 .
.
Ответ. 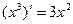 .
.
Задача 199. С помощью определения доказать, что 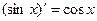 .
.
Решение. 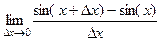 =
= 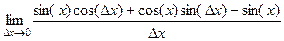 =
=
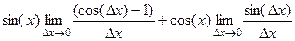 =
=
воспользуемся тригонометрической формулой понижения степени 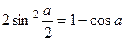 :
:
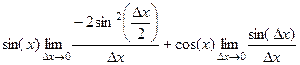 =
=
= 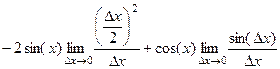 =
=
= 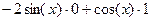 =
= 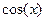 .
.
Ответ. 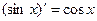 .
.
Задача 200. Вычислить производную от композиций:
А) 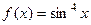 . Б)
. Б) 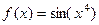
Решение. А) 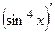 =
= 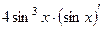 =
= 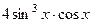 .
.
Б) 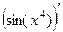 =
= 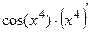 =
= 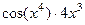 .
.
Ответы. 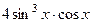 ;
; 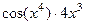 .
.
Задача 201. Найти производную от 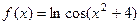 .
.
Решение. Здесь композиция трёх функций. Сначала действует степенная и переводит 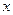 в
в 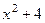 , затем вычисляется косинус, а от этого выражения зависит логарифм.
, затем вычисляется косинус, а от этого выражения зависит логарифм.
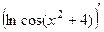 =
= 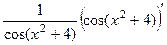 =
= 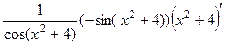 =
= 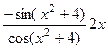 , что можно записать в виде
, что можно записать в виде 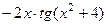 .
.
Ответ. 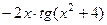 .
.
Задача 202. Найти производную функции 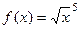 .
.
Решение. Способ 1. Можно рассматривать как композицию, тогда:
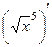 =
= 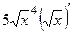 =
= 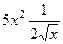 =
= 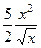 =
= 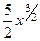 .
.
Способ 2. Можно рассматривать сразу как степенную функцию с дробной степенью, тогда решение такое: 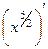 =
= 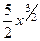 .
.
Как мы видим, двумя способами получаем одно и то же.
Ответ. 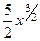 .
.
Задача 203. Найти 1 и 2 производную от 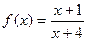 .
.
Решение. 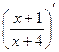 =
= 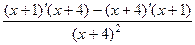 =
=
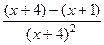 =
= 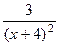 , что можно записать в виде
, что можно записать в виде  .
.
Вторая производная: 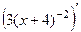 =
= 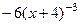 =
= 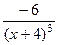 .
.
Ответ. 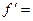
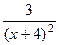
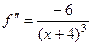 .
.
Задача 204. Найти производную от 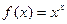 .
.
Решение. Здесь нельзя применять формулу степенной функции, ведь в показателе тоже есть переменная. Но нельзя и формулу показательной функции, т.к. в основании тоже есть переменная. Единственным выходом здесь является логарифмирование, чтобы 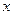 соатлось только в степени. Основание может быть представлено в виде
соатлось только в степени. Основание может быть представлено в виде 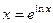 . Тогда
. Тогда 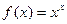 =
= 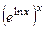 =
= 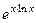 .
.
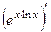 =
= 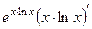 =
= 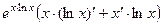 =
=
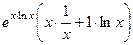 а теперь можем заменить обратно
а теперь можем заменить обратно 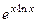 на
на 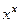 .
.
После приведения подобных, получим 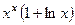 .
.
Ответ. 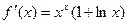 .
.
Задача 205. Найти производную вектор-функции 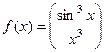 .
.
Решение. Производные двух координатных функций ищем независимо друг от друга.
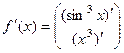 =
= 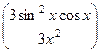 . Ответ.
. Ответ. 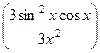 .
.
Задача 206. Найти 1-ю и 2-ю производную для 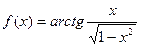 . Найти
. Найти 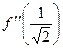 .
.
Решение. 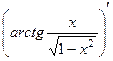 =
= 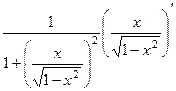 =
=
= 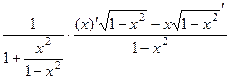 =
=
= 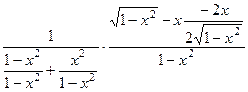 =
=
= 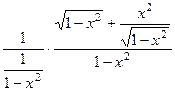 =
= 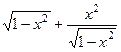 =
= 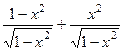 =
=
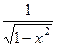 . Итак,
. Итак, 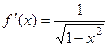 .
.
Следующая, 2-я производная:
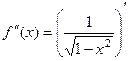 =
= 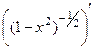 =
= 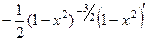 =
=
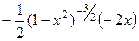 =
= 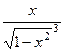 .
.
Вычислим «тестовое» значение при конкретном 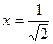 .
.
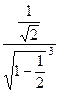 =
= 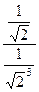 =
= 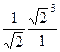 =
= 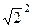 = 2.
= 2.
Ответ. 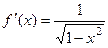 ,
, 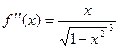 ,
, 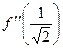 =2.
=2.
Задача домашняя. Найти 1-ю и 2-ю производную для 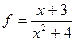 .
.
Решение. 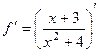 =
= 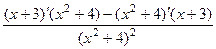 =
=
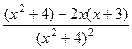 =
= 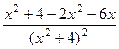 =
= 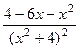 .
.
2-я производная: 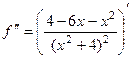 =
=
= 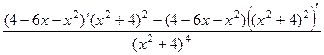 =
=
= 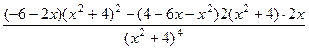 ,
,
сократим на 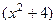 :
: 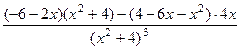 =
=
= 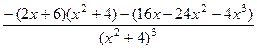 =
=
= 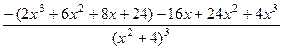 =
= 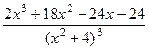 .
.
Ответ. 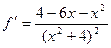
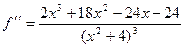
Задача 207. Найти производную от 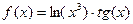 .
.
Решение. Здесь произведение, причём в одном из множителей есть композиция.
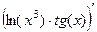 =
= 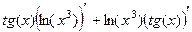 =
=
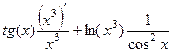 =
= 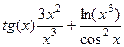 =
= 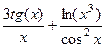 .
.
Ответ. 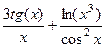 .
.
Задача 208. Найти 2-ю производную для 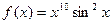 .
.
Решение. 1-я производная: 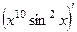 =
= 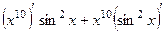 =
=
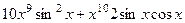 =
=  .
.
2-я производная: 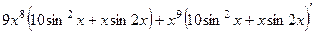 =
=
= 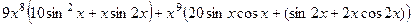 =
=
= 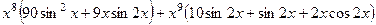 =
=
= 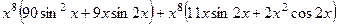 =
=
= 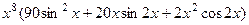 .
.
Ответ. 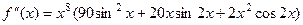 .
.
Задача 209. Вывести формулу 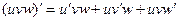 .
.
Решение. Объединим первые 2 слагаемых в один условный множитель, а третье пусть будет вторым множителем. После этого применим известную формулу, доказанную для 2 множителей.
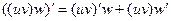 =
= 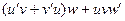 , что и приводит к
, что и приводит к
выражению 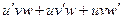 .
.
Задача 210. Найти 1-ю и 2-ю производную 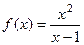 и
и 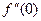 .
.
Решение. 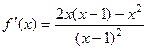 =
= 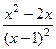 .
.
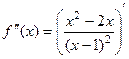 =
= 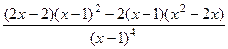 =
=
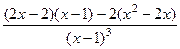 =
= 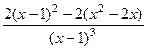 =
=
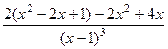 =
= 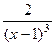 .
. 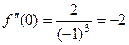 .
.
Ответ. 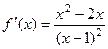 ,
, 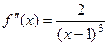 ,
, 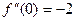 .
.
Задача 211. Дана функция 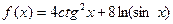 .
.
Найти 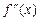 ,
, 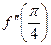 .
.
Решение. 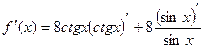 =
= 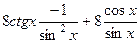 =
=
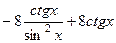 =
= 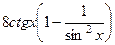 =
= 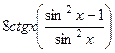 =
=
= 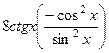 =
= 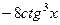 .
.
Максимально возможно привели подобные, чтобы затем было легче считать 2-ю производную.
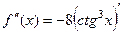 =
= 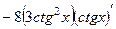 =
= 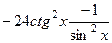 =
=
= 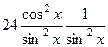 =
= 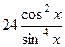 .
.
Вычислим 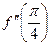 .
. 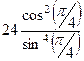 =
= 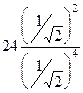 =
= 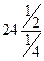 = 48.
= 48.
Ответ. 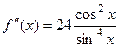 .
. 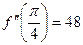 .
.
Задача 212. 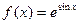 найти
найти 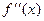 ,
, 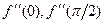 .
.
Решение. 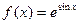 ,
, 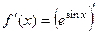 =
= 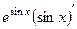 =
= 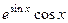 .
.
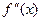 =
= 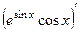 =
= 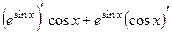 =
=
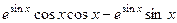 =
= 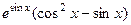 .
.
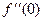 =
= 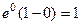 .
. 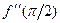 =
= 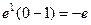 .
.
Ответ. 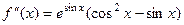 ,
, 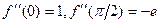 .
.
Задача 213.1. Нарисовать график 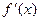 , если функция
, если функция 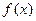 задана графически:
задана графически:
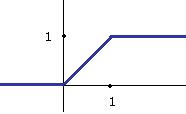
Решение. Здесь мы можем рассуждать следующим образом. Запишем функцию на каждом из участков:
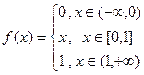
Тогда можно найти производную на каждом участке отдельно:
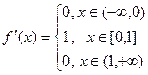
Тогда график производной выглядит так:
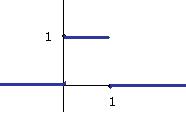
Задача 213.2. Нарисовать график 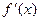 , если функция
, если функция 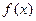 задана графически:
задана графически:
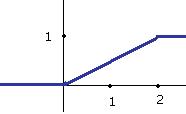
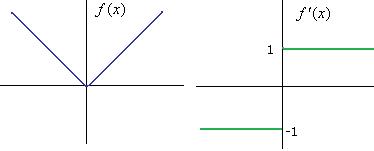
Здесь видно, что угловой коэффициент равен 0,5 при 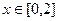 , на остальной части вещественной оси функция есть константа. Тогда график производной выглядит так (показано зелёным цветом).
, на остальной части вещественной оси функция есть константа. Тогда график производной выглядит так (показано зелёным цветом).
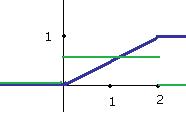
Мы видим, что в тех точках, где на исходном графике угол, производная имеет разрыв 1-го рода.
Возможны и другие варианты таких задач.
Задача 213.3. 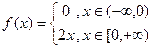
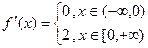
Задача 213.4. Если 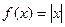 .
.
Задача 213.5. 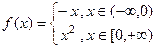
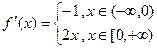
«Частные производные, градиент».
Задача 214. Дана функция 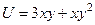 . Найти координаты вектора
. Найти координаты вектора 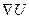 в точке
в точке 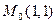 .
.
Решение. Найдём две частных производных.
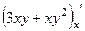 =
= 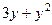 ,
, 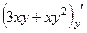 =
= 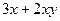 .
.
Градиент в произвольной точке: 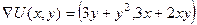 .
.
Кстати, для получившегося векторного поля функция 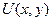 называется потенциалом.
называется потенциалом.
Градиент в точке 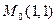 :
: 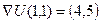 .
.
Ответ. 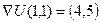 .
.
Задача 215. Дана функция 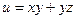 . Найти
. Найти 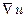 в точке
в точке 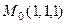 .
.
Решение.
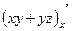 =
= 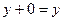 ,
, 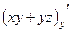 =
= 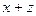 ,
, 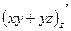 =
= 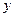 .
.
Градиент в произвольной точке: 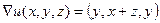 .
.
Градиент в точке 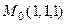 :
: 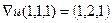 .
.
Ответ. 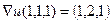 .
.
Задача 216. Найти градиент функции 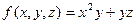 в точке (1,1,1).
в точке (1,1,1).
Решение. Найдём частные производные. 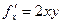 ,
, 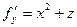 ,
, 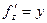 . Присвоим все значения x,y,z=1. Получаем
. Присвоим все значения x,y,z=1. Получаем 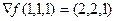 .
.
Ответ. 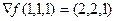 .
.
Задача 217. (На применение формулы полной производной).
Дано: 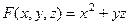 . Точка движется по прямой:
. Точка движется по прямой:
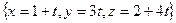 . Вычислить
. Вычислить 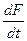 :
:
1) без формулы полной производной.
2) с помощью формулы полной производной.
Решение.
1 способ. Сведём к функции от 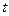 и вычислим для неё обычную производную.
и вычислим для неё обычную производную.
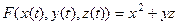 =
= 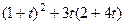 =
= 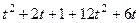 =
=
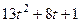 ,
, 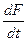 =
= 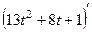 =
= 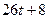 .
.
2 способ. По формуле полной производной: 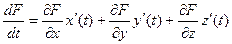 =
= 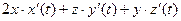 =
=
= 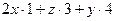 а теперь уже в этом выражении выразим
а теперь уже в этом выражении выразим 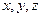 через
через 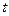 :
: 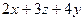 =
= 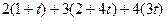 =
=
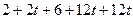 =
= 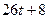 .
.
Ответ. 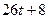 .
.
Алгоритм вычисления производной по направлению можно условно разделить на 4 шага:
1) Найти градиент в произвольной точке,
2) Найти градиент в конкретной точке,
3) Нормировать вектор, задающий направление,
4) Скалярно умножить градиент в точке на этот нормированный вектор.
Замечание. Шаги 3 и 4 перестановочны, то есть можно не нормировать вектор, а разделить на его длину получившееся скалярное произведение 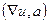 .
.
Задача 218. Дана функция 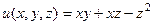 . Найти:
. Найти:
а) координаты вектора 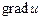 в точке
в точке 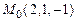 ,
,
б) 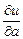 в точке
в точке 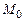 в направлении вектора
в направлении вектора 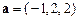 .
.
Решение. Найдём все 3 частных производных.
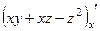 =
= 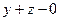 .
.
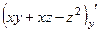 =
= 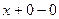 .
.
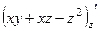 =
= 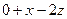 .
.
1) Градиент в произвольной точке: 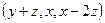 .
.
2) Градиент в точке 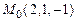 :
: 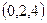 .
.
3) Нормируем вектор 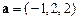 . Его длина
. Его длина 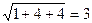 .
.
Нормированный вектор 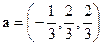 .
.
4) Скалярно умножим его на градиент в точке, т.е. 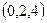 .
.
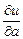 =
= 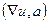 =
= 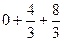 =
= 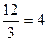 .
.
Ответ. 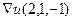 =
= 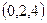 ,
, 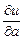 = 4.
= 4.
Задача 219. Дана функция 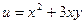 . Найти:
. Найти:
а) координаты вектора 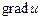 в точке
в точке 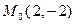 ;
;
б) 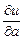 в точке
в точке 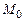 в направлении вектора
в направлении вектора 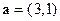 .
.
Решение. Ищем частные производные.
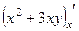 =
= 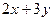 ,
, 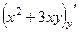 =
= 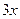 .
.
Итак, градиент 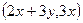 . При
. При 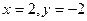 получаем вектор
получаем вектор 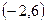 . Нормируем вектор
. Нормируем вектор 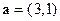 . Его длина
. Его длина 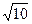 . Новый вектор
. Новый вектор
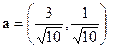 . Скалярно умножаем его на
. Скалярно умножаем его на 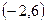 :
:
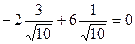 .
.
Ответ. 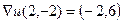 ,
, 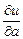 = 0.
= 0.
Задача 220. Найти градиент функции 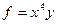 в точке (1,1) и производную по направлению (1,3).
в точке (1,1) и производную по направлению (1,3).
Решение. 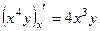 ,
, 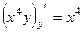 .
.
Градиент в произвольной точке: 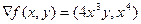
Градиент в конкретной точке: 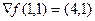
Нормируем вектор (1,3). 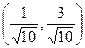 .
.
Скалярно умножим 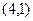 и
и 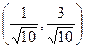 .
. 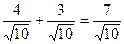 .
.
Ответ. 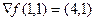 ,
, 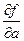 =
= 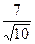 .
.
Задача 221. Дана функция 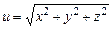 . Найти:
. Найти:
а) координаты вектора 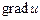 в точке
в точке 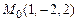
б) 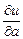 в точке
в точке 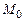 в направлении вектора
в направлении вектора 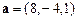 .
.
Решение. Частные производные:
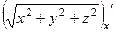 =
= 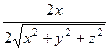 =
= 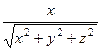 . Аналогично
. Аналогично
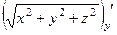 =
= 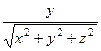 ,
, 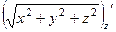 =
= 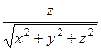 .
.
Присвоим конкретные значения 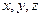 и получим градиент в точке.
и получим градиент в точке.
Учитывая, что 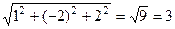 ,получится:
,получится:
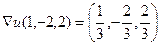 .
.
Нормируем вектор 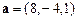 . Его длина
. Его длина 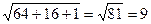 .
.
Итак, надо рассматривать такой вектор: 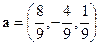 .
.
Теперь скалярно умножим его на градиент.
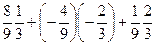 =
= 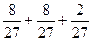 =
= 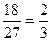 .
.
Ответ. 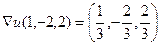 ,
, 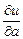 =
= 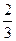 .
.
Задача 222. Найти градиент функции 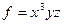 в точке
в точке 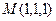 и производную по направлению
и производную по направлению 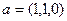 .
.
Решение.
1) Вычисляем частные производные: 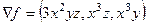 .
.
2) 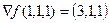 .
.
3) Скалярно умножаем 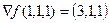 на
на 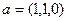 , получим 4.
, получим 4.
4) Разделим на 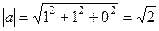 , получим
, получим 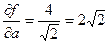 .
.
Ответ. 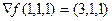 ,
, 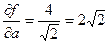 .
.
* Задача домашняя. Найти градиент функции 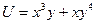 в точке (2,2) и производную по направлению a = (3,4).
в точке (2,2) и производную по направлению a = (3,4).
Решение. 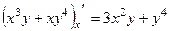 ,
, 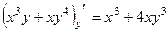 .
.
Градиент в произвольной точке: 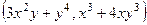 .
.
Градиент в точке (2,2) равен 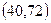 .
.
Нормируя вектор (3,4) получаем 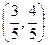 .
.
Скалярно умножаем 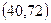 и
и 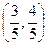 .
. 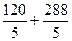 =
= 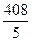 = 81,6.
= 81,6.
Ответ. Градиент 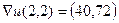 ,
, 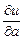 = 81,6.
= 81,6.
Задача 223. Найти градиент функции 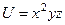 в точке (1,2,3) и производную по направлению a = (1,0,1).
в точке (1,2,3) и производную по направлению a = (1,0,1).
Решение.
1. 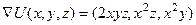 .
.
2. 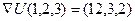
3. Нормируем вектор a = (1,0,1). Его модуль 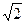 . Тогда нормированный вектор:
. Тогда нормированный вектор: 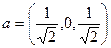 .
.
4. Скалярно умножим 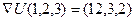 на
на 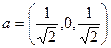 .
.
Получим 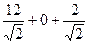 =
= 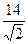 =
= 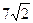 .
.
Ответ. 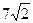 .
.
«Уравнение касательной».
Вспомнить уравнение: 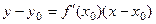 .
.
Задача 224. Найти касательную к графику 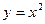 в точке
в точке 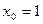 .
.
Решение. 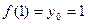 ,
, 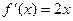 ,
, 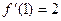 . Уравнение
. Уравнение 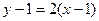 , то есть
, то есть 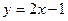 .
.
Ответ. 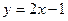 .
.
Задача 225. Найти уравнение касательной к кривой 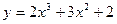 в точке
в точке 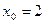 .
.
Решение. Значение в точке: 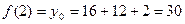 .
.
Производная: 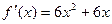 .
.
Производная в точке: 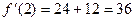 .
.
Уравнение 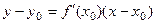 принимает вид
принимает вид 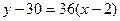 ,
,
что преобразуется к виду 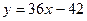 .
.
Ответ. 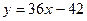 .
.
Задача 226. Найти касательную к графику 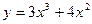 в точке
в точке 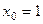 .
.
Решение. 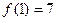 ,
, 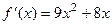 ,
, 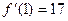 .
.
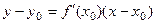
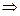
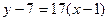
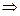
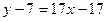
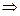
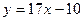 .
.
Ответ. Уравнение касательной 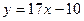 .
.
Задача 227. Найти касательную к графику 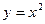 в точке с абсциссой 2 и расстояние от этой прямой до начала координат.
в точке с абсциссой 2 и расстояние от этой прямой до начала координат.
Решение. 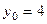 ,
, 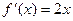 ,
, 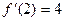 .
.
Подставим эту информацию в уравнение 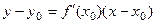 .
.
Получается 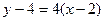
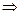
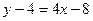
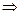
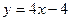 .
.
Надо применить формулу расстояния от точки до прямой в плоскости:
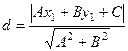
для этого сначала преобразуем к неявному виду: 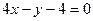 .
.
Тогда видно, что 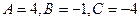 .
. 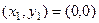 .
.
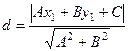 =
= 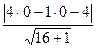 =
= 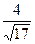 .
.
Ответ. Касательная 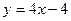 , расстояние
, расстояние 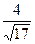 .
.
Задача 228. Найти касательную к графику функции 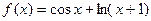 в точке
в точке 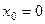 .
.
Решение. 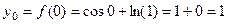 .
.
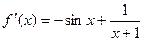 .
. 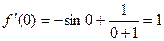 .
.
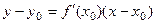
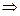
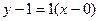
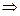
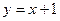 .
.
Ответ. Уравнение касательной 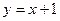 .
.
Задача 229. Найти уравнение касательной к графику 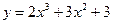 в точке
в точке 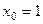 и площадь треугольника, который она отсекает от одной из координатных четвертей.
и площадь треугольника, который она отсекает от одной из координатных четвертей.
Решение. 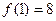 ,
, 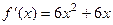 ,
, 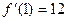 .
.
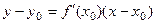
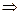
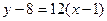
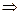
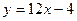 .
.
Выясним, треугольник и в какой четверти она отсекает. Для этого найдём точки пересечения с координатными осями.
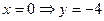 ,
, 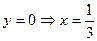 . Точки
. Точки 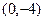 и
и 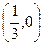 . Треугольник в 4-й четверти. Схематично покажем, где и как он расположен:
. Треугольник в 4-й четверти. Схематично покажем, где и как он расположен:
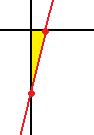
Его площадь это 0,5 от площади достроенного прямоугольника, а она была бы равна 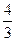 . Поэтому ответ
. Поэтому ответ 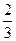 .
.
Ответ. Касательная 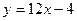 , площадь треугольника
, площадь треугольника 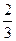 .
.
Задача 230. На графике функции 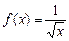 взята точка
взята точка 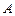 . Касательная к графику в точке
. Касательная к графику в точке 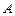 наклонена к оси
наклонена к оси


