Число маршрутов в модулях циклических программ

Рассмотрим влияние зависимости фрагментов на критерий сложности модулей по Липаеву, то есть на число маршрутов в модулях. В дальнейшем под термином “маршрут” (“путь”) будем подразумевать так называемые условные (объясняется ниже) маршруты (пути).

Обозначим S - общее число маршрутов (путей) в модуле, а Sn - число путей в n-ом фрагменте этого модуля.

Пусть модуль содержит только зависимые фрагменты (рис. 3). Управляющий граф [1] этого модуля изображен на рис. 4,а, из которого следует, что фрагмент 1 содержит 5 маршрутов, а фрагмент 2 - 3 маршрута. Так как каждый маршрут фрагмента 2 зависит от маршрутов фрагмента 1, то общее число маршрутов в данном модуле равно произведению чисел маршрутов каждого из фрагментов, то есть S = S1 * S2.

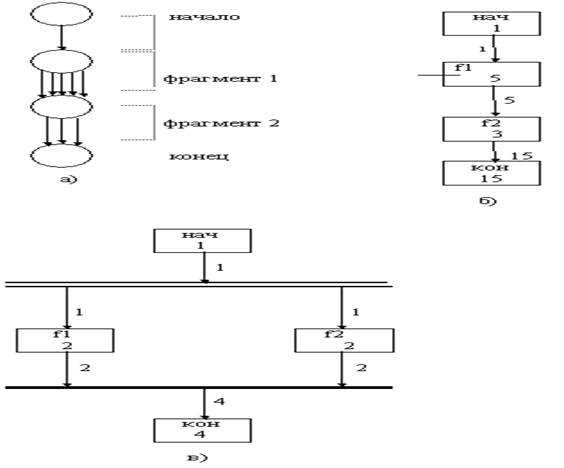Рис.4. Расчетные маршрутные схемы (РМС):

а) управляющий граф модуля по рис.3,

б) РМС этого модуля,

в) РМС модуля по рис. 2,в.

Управляющий граф не очень удобен для рисования и подсчета общего числа маршрутов модулей, фрагменты которых содержат сравнительно большое число путей каждый. Поэтому вместо управляющего графа предлагается более простая расчетная маршрутная схема (РМС) модуля (рис.4,б). В РМС прямоугольниками обозначены: оператор начала - “нач”, оператор конца - “кон”, фрагмент n - “fn”. В нижней части прямоугольника, обозначающего фрагмент, указано число путей в данном фрагменте; в нижней части прямоугольника,обозначающего начало модуля указана константа единица. Рядом с дугой, соединяющей два прямоугольника, указывается число маршрутов, образованных всеми фрагментами, размещенными последовательно от начала модуля до того фрагмента, в который входит рассматриваемая дуга. В нижней части прямоугольника,обозначающего конец модуля, указывается общее число путей в модуле. Фрагменты, имеющие единственный путь в РМС не включаются.

В общем случае, общее число S путей последовательности из N зависимых фрагментов определяется следующим образом:

S = S1 * S2 * ... * SN, где знак “*” обозначает операцию произведения.

Рассмотрим теперь независимые фрагменты. Как уже упоминалось, независимые фрагменты могут быть реализованы параллельно. Любой маршрут независимого фрагмента не связан с другими фрагментами модуля, поэтому он анализируется автономно. На рис. 4,в показана РМС модуля с двумя независимыми фрагментами. Для модуля с независимыми фрагментами РМС выполняется в варианте параллельного соединения фрагментов даже, если модуль реализован с последовательным включением этих фрагментов. Числа, указанные в РМС на рис.4,в интерпретируются так же, как и на рис. 4,б. Дополнительно поясним: дуги, исходящие из двойной черты (распараллеливание процесса) отмечены тем же числом, что и заходящая в двойную черту дуга; дуга, исходящая из жирной горизонтальной черты, обозначающей конец распараллеливания, отмечается числом, равным сумме чисел, помечающих заходящие в эту черту дуги. Тем самым устанавливается следующий факт.: общее число S анализируемых путей модуля, содержащего только независимые фрагменты, определяется суммой вида S = S1 + S2 + ... + SN, где N - число независимых фрагментов. Однако, реальный путь в последовательной программе проходит через все фрагменты, невзирая на их независимость. Поэтому число R реальных путей равно числу путей S, вычисленному из той посылки, что независимых фрагментов в модуле нет.

Отметим, что пути в РМС с параллельным включением независимых фрагментов будем называть условными, а величину S - числом условных (по умолчанию) путей, в отличие от величины R - числа реальных путей в МЦП. При этом S < R.

Практически МЦП, включающие только независимые или только зависимые фрагменты встречаются достаточно редко. Для расчета числа анализируемых путей в МЦП с фрагментами обоих типов сначала устанавливается взаимозависимость фрагментов и групп фрагментов, что покажем на примере.

На рис. 5,а представлен модуль из девяти фрагментов, последовательно размещенных в соответствии с текстом последовательно реализуемой подпрограммы. Через дробь после обозначения фрагмента указано число путей в нем. Отметим, что произвольная группа следующих подряд фрагментов так же является фрагментом, который будем обозначать перечислением в скобках обозначений составляющих группу фрагментов. Пусть, например, имеет место следующая зависимость фрагментов в модуле (рис. 5,а): фрагменты (f1,f2,f3) и (f4,f5,f6,f7,f8,f9) независимы относительно начала и конца, фрагмент f3 сверху зависим от f1 (f2), фрагменты f1 и f2 независимы относительно начала и фрагмента f3, фрагмент f5 сверху зависим от f4, фрагмент (f6,f7) сверху зависим от f5, фрагмент (f8,f9) сверху зависим от f6 (f7), фрагменты f6 и f7 независимы относительно f5 и (f8,f9), фрагменты f8 и f9 независимы относительно (f6,f7) и конца.

Рис.5. Модуль с зависимыми и относительно независимыми фрагментами (а) и его РМС (б).

На основании изложенного получена РМС (рис. 5,б) и расчитано общее число условных путей в модуле (рис. 5,а) S = 1545, в то время как реальное число путей

R = 10 * 5 * 7 * 4 * 6 * 2 * 3 * 5 * 7 = 1764000

Данное число на три порядка (!) превосходит ранее полученное.

Таким образом независимость фрагментов позволяет значительно снизить число анализируемых (условных) маршрутов в МЦП, а РМС облегчает соответствующий расчет.

Введем для МЦП коэффициент Kn независимости: Кn = S / R. Он имеет пределы: верхний, равный единице, (все фрагменты зависимые) и нижний, равный отношению суммы числа путей фрагментов к R (все фрагменты независимы).