 |
Главная |
Поле комплексных чисел
|
из
5.00
|
Вопросы поля комплексных чисел, описывается построение поля комплексных чисел, приводятся алгебраическая форма записи комплексных чисел, определение комплексного числа, действия над комплексными числами.
п.1. Построение поля комплексных чисел.
Рассмотрим множество 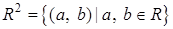 . Определим на
. Определим на 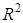 бинарные операции сложения
бинарные операции сложения 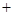 , умножения
, умножения 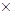 , унарную операцию
, унарную операцию 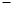 и определим элементы
и определим элементы 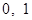 .
.
Для 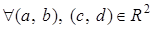 :
:
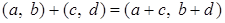 ;
;
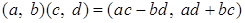 ;
;
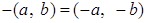 .
.
Обозначим: 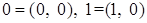 .
.
Теорема 1. Алгебра 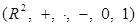 является полем.
является полем.
Доказательство. Проверим, что алгебра 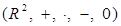 есть абелева группа.
есть абелева группа.
Для 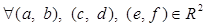
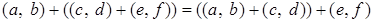 .
.
Для 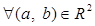
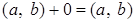 .
.
Для 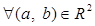
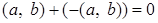 .
.
Для 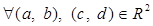
( 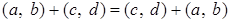 .
.
Проверим, что операция 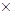 - ассоциативна, то есть
- ассоциативна, то есть 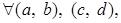
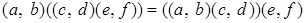 .
.
Действительно,
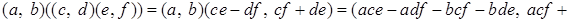
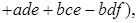
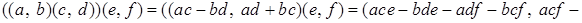
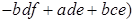 .
.
Проверим левый закон дистрибутивности, то есть для 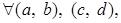
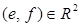
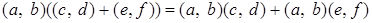 .
.
Действительно,
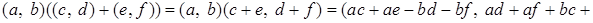
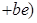 ,
,
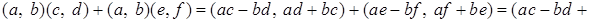
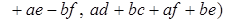 .
.
Аналогично проверяется справедливость правого закона дистрибутивности.
Из выше доказанного следует, что алгебра 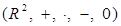 есть кольцо.
есть кольцо.
Проверим, что кольцо 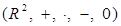 коммутативно, то есть для
коммутативно, то есть для 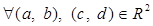
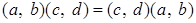 .
.
Действительно,
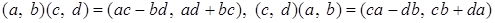 .
.
Проверим, что 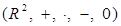 - кольцо с единицей 1, то есть
- кольцо с единицей 1, то есть 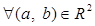
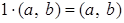 .
.
Действительно,
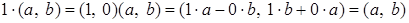 .
.
Так как 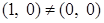 , то
, то 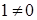 .
.
Докажем, что каждый ненулевой элемент кольца 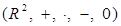 обратим. Пусть
обратим. Пусть 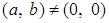 , что равносильно
, что равносильно 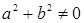 . Рассмотрим пару
. Рассмотрим пару 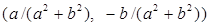 и проверим, что эта пара является обратной к паре
и проверим, что эта пара является обратной к паре 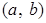 . Действительно,
. Действительно,
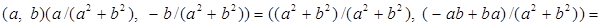
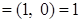 .
.
Из выше доказанного следует, что алгебра 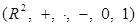 - поле.
- поле.
Определение. Поле 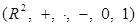 называется полем комплексных чисел, а его элементы - комплексными числами.
называется полем комплексных чисел, а его элементы - комплексными числами.
п.2. Алгебраическая форма записи комплексных чисел.
Обозначение. Множество комплексных чисел принято обозначать 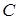 , то есть
, то есть 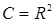 . Приняты также следующие обозначения:
. Приняты также следующие обозначения:
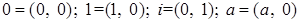 для
для 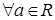 .
.
Теорема 2. Каждое комплексное число 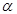 может быть, и притом единственным образом, записано в виде:
может быть, и притом единственным образом, записано в виде:
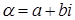 , где
, где 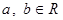 . (Такая запись называется алгебраической формой записи комплексного числа
. (Такая запись называется алгебраической формой записи комплексного числа 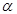 ).
).
Доказательство. Существуют 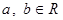 такие, что
такие, что 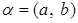 . Имеем
. Имеем
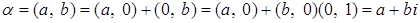 .
.
Теорема 3. Число 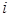 обладает свойством:
обладает свойством: 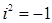 .
.
Доказательство. 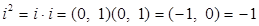 .
.
Из равенства 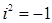 следует, что
следует, что 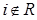 .
.
Определение. Пусть 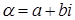 , где
, где 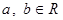 . Число
. Число 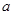 называется действительной частью,
называется действительной частью, 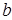 - мнимой частью комплексного числа
- мнимой частью комплексного числа 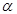 . Пишем
. Пишем 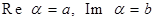 .
.
Пусть 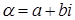 - алгебраическая форма записи комплексного числа
- алгебраическая форма записи комплексного числа 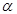 . Тогда:
. Тогда:
если 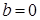 , то
, то 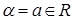 ;
;
если 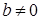 , то
, то 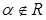 .
.
Определение. Если 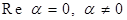 , то комплексное число
, то комплексное число 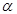 называют чисто мнимым числом.
называют чисто мнимым числом.
Действия над комплексными числами в алгебраической форме
1) Для 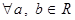
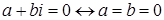 .
.
Другими словами: комплексное число равно нулю тогда и только тогда, когда у него действительная и мнимая части равны нулю.
Доказательство. 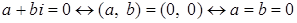 .
.
2) Для 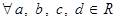
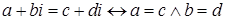 .
.
Другими словами: два комплексных числа равны тогда и только тогда, когда у них, соответственно, равны действительная и мнимая части.
Доказательство. 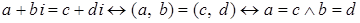 .
.
3) Для 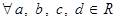
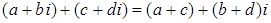 .
.
Другими словами: чтобы сложить два комплексных числа, нужно, соответственно, сложить их действительные и мнимые части.
Доказательство. 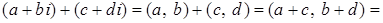
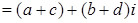 .
.
4) Для 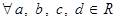
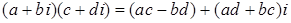 .
.
Доказательство. 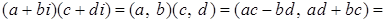
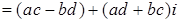 .
.
5) Для 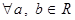
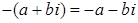 .
.
Доказательство. 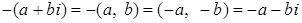 .
.
6) Для 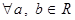 , если
, если 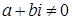 , то
, то
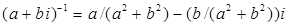 .
.
Доказательство. 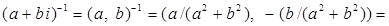
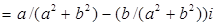 .
.
п.3. Операция сопряжения.
Определение. Пусть комплексное число 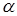 записано в алгебраической форме
записано в алгебраической форме 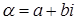 . Числом сопряжённым с
. Числом сопряжённым с 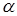 называется число
называется число 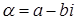 .
.
Свойства операции сопряжения
Для 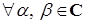 , где
, где 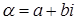 ,
, 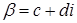 ,
, 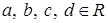 .
.
1).
Доказательство.
.
2) .
Доказательство. .
3) .
Доказательство.
.
.
4) Если a ¹ 0, то 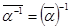 .
.
Доказательство. 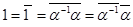 .
.
5) 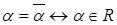 .
.
Доказательство. 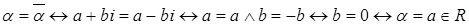 .
.
6) 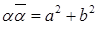 .
.
Доказательство. 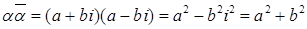 .
.
С помощью операции сопряжения удобно производить деление комплексных чисел. Чтобы записать в алгебраической форме дробь с комплексными числителем и знаменателем нужно умножить числитель и знаменатель дроби на число, сопряжённое со знаменателем, и вычислить произведения в числителе и знаменателе.
п.4. Модуль комплексного числа.
Пусть 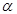 записано в алгебраической форме
записано в алгебраической форме 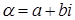 .
.
Определение. Модулем комплексного числа 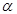 называется неотрицательное действительное число
называется неотрицательное действительное число 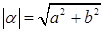 .
.
Свойства модуля.
Для 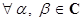 , где
, где 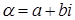 ,
, 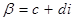 ,
, 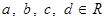 .
.
1)  .
.
Доказательство. 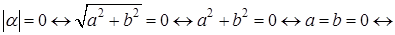
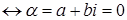 .
.
2) 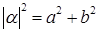 .
.
3) 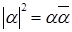 .
.
Доказательство. Свойство следует из свойства 6 операции сопряжения.
4) 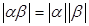 .
.
Доказательство. 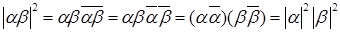 .
.
Отсюда следует нужное утверждение.
5) Если 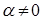 , то
, то 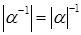 .
.
Доказательство. 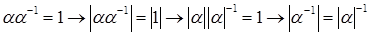 .
.
6) Неравенство треугольника: 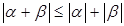 .
.
Доказательство. Докажем сначала неравенство
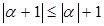 .
.
Имеем
(2) 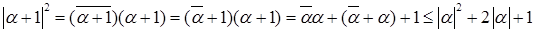 ,
,
так как
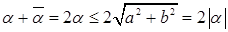 .
.
Из (2) следует, что
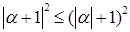 .
.
Из последнего неравенства следует неравенство (1).
Докажем теперь неравенство треугольника. Неравенство треугольника, очевидно, выполнено для 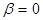 . Докажем неравенство треугольника для
. Докажем неравенство треугольника для 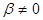 . Имеем
. Имеем
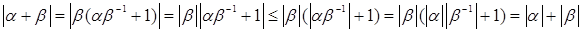 .
.
7) 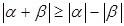 .
.
Доказательство. 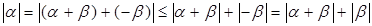 . Отсюда следует нужное неравенство.
. Отсюда следует нужное неравенство.
8) 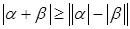 .
.
Доказательство. Справедливы неравенства
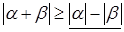 ,
, 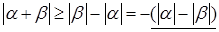 .
.
Одно из подчёркнутых чисел совпадает с 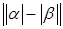 .
.
п.5. Геометрическая интерпретация комплексных чисел.
Пусть 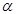 записано в алгебраической форме
записано в алгебраической форме 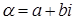 . Поставим в соответствие числу
. Поставим в соответствие числу 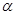 точку плоскости с координатами
точку плоскости с координатами 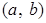 . Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью.
. Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью.
Числа 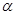 и
и 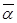 расположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел.
расположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел.
Геометрический смысл модуля
Из Рис.1 видно, что расстояние от начала координат до числа 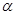 равно
равно 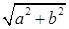 . Поэтому геометрический смысл
. Поэтому геометрический смысл 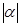 - расстояние от
- расстояние от 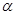 до начала координат.
до начала координат.
y

 bi a
bi a
i
 -1+i 1+i
-1+i 1+i
 - 1 0 1 a
- 1 0 1 a
x
- 1-i 1-i
- i
Рис.1.
 - bi `a
- bi `a
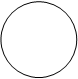
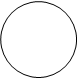
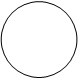
Пример. Изобразим на комплексной плоскости, на Рис.2, множества, заданные, соответственно, следующими условиями: 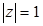 ;
; 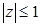 ;
; 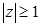 .
.
 |  |  |


 y | z | =1 y | z | £1 y | z | ³1
y | z | =1 y | z | £1 y | z | ³1














 i i i
i i i






 - 1 1 - 1 1 - 1 1
- 1 1 - 1 1 - 1 1









 0 0 0
0 0 0












- i - i - i
Рис.2.
Пусть 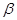 записано в алгебраической форме
записано в алгебраической форме 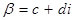 . Имеем
. Имеем
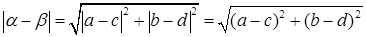 .
.
Из Рис.3 видно, что геометрический смысл модуля разности комплексных чисел - расстояние между этими числами.
 y
y

 b a
b a

d |b-d|



 b |a-c|
b |a-c|
Рис.3.
0 c a x
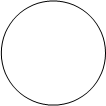
Пример. Изобразим на комплексной плоскости, на Рис.4, множества, заданные, соответственно, следующими условиями: 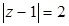 ;
; 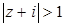 .
.
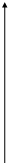
 y y
y y

 | z-1| =2 0
| z-1| =2 0
x
- i
- 1 0 1 3 x |z+i | > 1
- 2i
Рис.4.
Геометрическая интерпретация комплексных чисел векторами плоскости
Поставим в соответствие числу 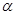 связаный вектор плоскости с началом в начале координат и с концом в точке
связаный вектор плоскости с началом в начале координат и с концом в точке 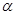 . Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.
. Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.
 y
y

 a+b
a+b
 b
b

 a
a
0 Рис.5
x
Геометрический смысл модуля комплексного числа 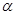 , при интерпретации чисел векторами, - длина вектора
, при интерпретации чисел векторами, - длина вектора 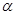 . Сумма комплексных чисел находится как сумма векторов.
. Сумма комплексных чисел находится как сумма векторов.
п.6. Тригонометрическая форма записи комплексного числа.
Определение. Аргументом комплексного числа 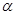 называется число
называется число 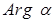 , равное величине угла между положительным направлением оси абсцисс и вектором
, равное величине угла между положительным направлением оси абсцисс и вектором 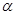 ,
, 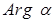 определяется с точность до углов, кратных
определяется с точность до углов, кратных 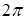 . Главным значением аргумента комплексного числа
. Главным значением аргумента комплексного числа 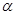 называется то значение
называется то значение 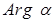 , которое принадлежит промежутку
, которое принадлежит промежутку 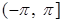 , оно обозначается
, оно обозначается 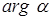 и
и 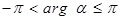 .
.
Пусть 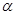 записано в алгебраической форме
записано в алгебраической форме 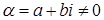 . Тогда из геометрической интерпретации
. Тогда из геометрической интерпретации 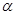 следует, что:
следует, что:
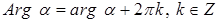 ;
;
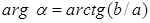 , если
, если 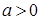 ;
;
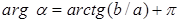 , если
, если 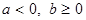 ;
;
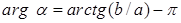 , если
, если 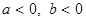 .
.
Заметим, что 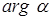 выражается только в радианах,
выражается только в радианах, 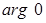 не определён.
не определён.
Теорема 4. Каждое комплексное число 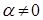 может быть записано в виде
может быть записано в виде
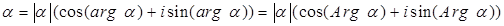 .
.
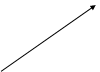
Доказательство. Изобразим 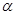 вектором комплексной плоскости,
вектором комплексной плоскости,
см. Рис.6.




y
b a
Рис.6.
0 a x
Угол, образованный вектором 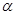 и положительным направлением оси абсцисс, равен
и положительным направлением оси абсцисс, равен 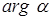 , следовательно,
, следовательно, 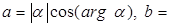
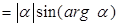 . Поэтому
. Поэтому 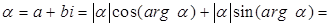
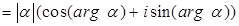 .
.
Определение. Если комплексное число 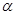 записано в виде
записано в виде 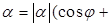
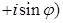 , то говорят, что
, то говорят, что 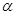 записано в тригонометрической форме.
записано в тригонометрической форме.
Правила действий с комплексными числами, записанными в тригонометрической форме.
Пусть комплексные числа 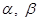 записаны в тригонометрической форме
записаны в тригонометрической форме
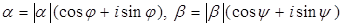 .
.
1) 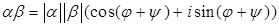 ,
,
то есть при умножении комплексных чисел, записанных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
Доказательство.
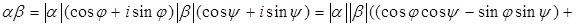
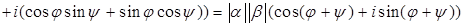 .
.
2) Если 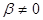 , то
, то
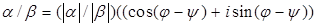 ,
,
то есть при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Доказательство. Обозначим 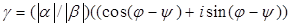 . Так как
. Так как 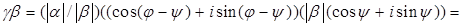
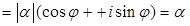 , то нужное утверждение доказано.
, то нужное утверждение доказано.
3) Если 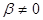 , то
, то
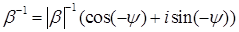 .
.
4) Формула Муавра. Для 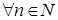 ,
,
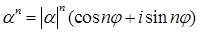 .
.
Доказательство. Формула Муавра является следствием правила 1.
5) Обобщённая формула Муавра. Для 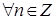 ,
,
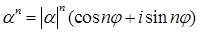 .
.
Доказательство. Обобщённая формула Муавра является следствием формулы Муавра и свойства 3).
п.7. Показательная форма записи комплексного числа.
Обозначение. Для 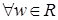 обозначим
обозначим
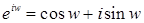 . (1)
. (1)
Равенство (1) называют формулой Эйлера. При этом обозначении, запись комплексного числа 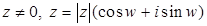 в показательной форме принимает вид
в показательной форме принимает вид
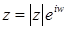 . (2)
. (2)
Из равенства (1) и правил действия с комплексными числами, записанными в тригонометрической форме, следует справедливость следующей теоремы .
Теорема 5. Для 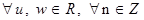 справедливы равенства:
справедливы равенства:
1) 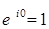 ;
;
2) 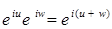 ;
;
3) 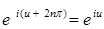 ;
;
4) 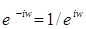 ;
;
5) 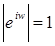 ;
;
6) 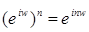 ;
;
7) 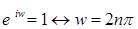
п.8. Связь между тригонометрическими и гиперболическими функциями.
Из формул Эйлера следует, что для 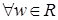
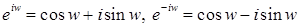 .
.
Складывая и вычитая эти равенства находим, что для 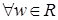 :
:
(1) 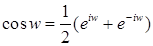 ;
;
(2) 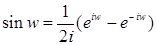 .
.
Как известно, из курса математического анализа, гиперболические косинус, синус, тангенс, котангенс, соответственно, 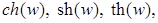
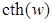 , для
, для 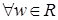 , определяются равенствами:
, определяются равенствами:
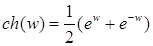 ;
; 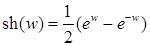 ;
;
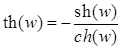 ;
; 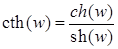 .
.
Если в формулах (1), (2), заменить 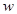 на
на 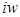 , то мы получим формулы для определения значений
, то мы получим формулы для определения значений 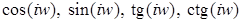 . Эти формулы выражают гиперболические формулы через тригонометрические. Для
. Эти формулы выражают гиперболические формулы через тригонометрические. Для 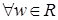 :
:
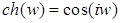 ;
; 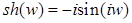 ;
;
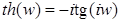 ;
; 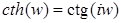 .
.
п.9. Корни из комплексных чисел.
Определение. Пусть 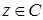 ,
, 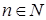 . Комплексное число
. Комплексное число 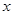 называется корнем степени
называется корнем степени 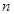 из
из 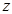 , если
, если 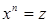 .
.
Теорема 6. Пусть 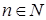 ,
, 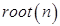 - множество всех корней степени
- множество всех корней степени 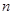 из 1. Тогда алгебра
из 1. Тогда алгебра 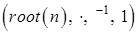 - группа, (которая называется группой корней степени
- группа, (которая называется группой корней степени 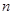 из 1).
из 1).
Доказательство. Пусть 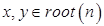 .
.
Проверим, что умножение – бинарная операция. Имеем 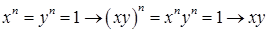 - корень степени
- корень степени 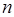 из 1.
из 1.
Проверим, что 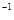 - унарная операция. Имеем
- унарная операция. Имеем 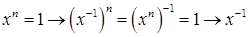 - корень степени
- корень степени 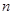 из 1.
из 1.
Очевидно, что 1 – корень степени 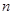 из 1.
из 1.
Доказано, что 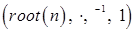 - алгебра.
- алгебра.
То, что алгебра 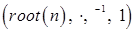 - группа, следует из свойств комплексных чисел.
- группа, следует из свойств комплексных чисел.
Теорема 7. Для 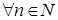 существует точно
существует точно 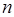 различных корней
различных корней 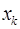 степени
степени 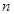 из 1,
из 1, 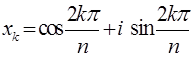 ,
, 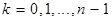 . (1)
. (1)
Все корни расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0).
Доказательство. Проверим сначала, что числа 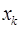 , заданные равенством (1), являются корнями степени
, заданные равенством (1), являются корнями степени 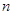 из 1. Действительно,
из 1. Действительно, 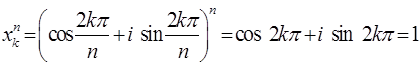 .
.
Докажем, что любой корень 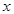 степени
степени 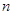 из 1 может быть вычислен по формуле (1). Т.к.
из 1 может быть вычислен по формуле (1). Т.к.  , то
, то 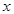 можно записать в показательой форме
можно записать в показательой форме 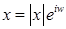 .
.
Имеем 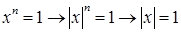 . Поэтому
. Поэтому 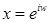 ,
, 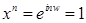 ,
, 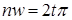 , где
, где 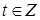 . По теореме о делении с остатком, существуют такие
. По теореме о делении с остатком, существуют такие 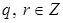 , что
, что 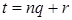 , где
, где 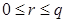 .
.
Значит, 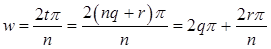 ,
, 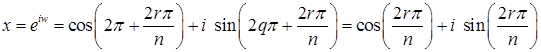 , т.е. вычисляется по формуле (1).
, т.е. вычисляется по формуле (1).
Изобразив числа, заданные формулой (1), на комплексной плоскости, мы увидим, что они расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0). В частности, числа, заданные формулой (1), попарно различны.
Теорема 8. Пусть 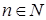 ,
, 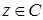 ,
, 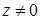 ,
, 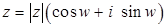 . Тогда существует точно
. Тогда существует точно 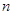 различных корней
различных корней 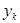 степени
степени 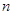 из
из 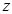 ,
, 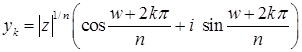 ,
, 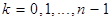 . (2)
. (2)
Доказательство. Проверим сначала, что числа 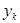 , заданные равенством (2), являются корнями степени
, заданные равенством (2), являются корнями степени 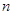 из
из 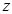 . Действительно,
. Действительно, 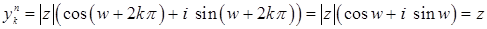 .
.
Пусть 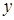 - корень степени
- корень степени 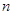 из
из 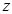 . Докажем, что он вычисляется по формуле (2). Рассмотрим число
. Докажем, что он вычисляется по формуле (2). Рассмотрим число 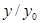 , где
, где 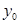 определено формулой (2). Имеем
определено формулой (2). Имеем 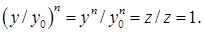
Следовательно 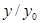 - корень степени
- корень степени 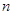 из 1, т.е.
из 1, т.е. 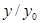 совпадает с одним из чисел
совпадает с одним из чисел 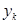 . Имеем
. Имеем 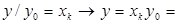
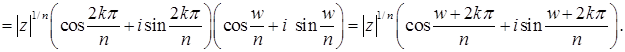
Из вышедоказанного следует, что числа 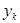 попарно различны.
попарно различны.
п.10. Мультисекция.
Теорема 1. (о мультисекции многочлена) Пусть
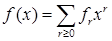 - многочлен с числовыми коэффициентами,
- многочлен с числовыми коэффициентами, 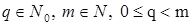 . Тогда
. Тогда
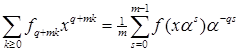 , (1)
, (1)
где 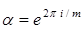 .
.
Доказательство. Для 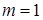 равенство (1) очевидно выполнено. Докажем (1) для
равенство (1) очевидно выполнено. Докажем (1) для 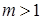 . Имеем
. Имеем
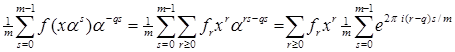 (2)
(2)
Если - целое, то 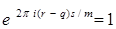 и
и 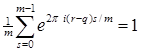 .
.
Если - не целое, то 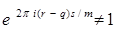 и по формуле суммы членов геометрической прогрессии
и по формуле суммы членов геометрической прогрессии
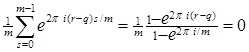 .
.
Поэтому в (2) суммирование нужно вести только по тем 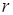 , для которых
, для которых 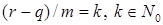 . Отсюда следует (1).
. Отсюда следует (1).
Заметим, что равенство (1) справедливо не только для многочленов, но и для рядов.
Следствие 1. Пусть
|
из
5.00
|
Обсуждение в статье: Поле комплексных чисел |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

