Теорема о несвязных классах видимости.

Несвязный класс видимости состоит из конечного числа l ≥3 связных непересекающихся компонент M₁,...,M _l, каждая из которых может быть либо точкой, либо отрезком, либо выпуклым многоугольником. При этом существует n≤l(l-1)/2 связных классов видимости K₁,...,K _n таких, что каждая компонента M _i является пересечением m _i этих связных классов, где 2≤m _i ≤l-1.

Если понятие ядра видимости является более "экзотическим" (ядро видимости, как несложно заметить, имеет меру нуль, поскольку располагается на некотором касательном отрезке), то понятие класса видимости имеет более богатый спектр приложений. Покрытие террайна конечным числом классов или предклассов видимости используется для представления среды в виде графа районов [14], которые и могут выявляться на основе такого покрытия. Эти же покрытия применяются для навигационных вычислений. Наличие несвязных классов видимости свидетельствует о существовании специфической конфигурации для групп роботов, получившей в работах [14] название "райского сада". Любую задачу выбора пути можно решить с точностью до класса видимости.

Следует особо отметить, что в районе расположения ядер группа МР может совершать маневры типа "движение в ядре", когда в каждый момент времени роботы находятся в одном из ядер (при этом они могут продвигаться вперед к подцели движения), а поля зрения у МР будут совпадать.

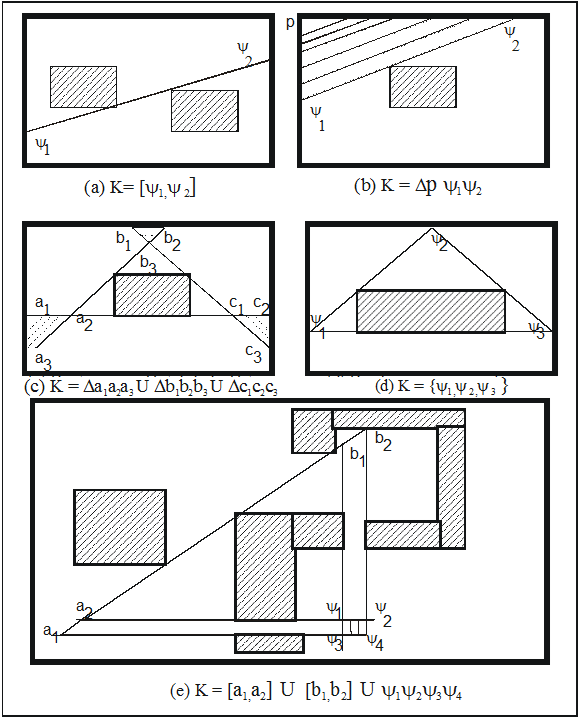
Рис. 6. Атлас классов: (a,b) - связные классы, (c,d,e) - несвязные.

 

Доказательство теорем приведено в [14]. Рис. 6,7 иллюстрируют вышесказанное. На рис.7 приведены примеры характеристик несвязного класса.

 

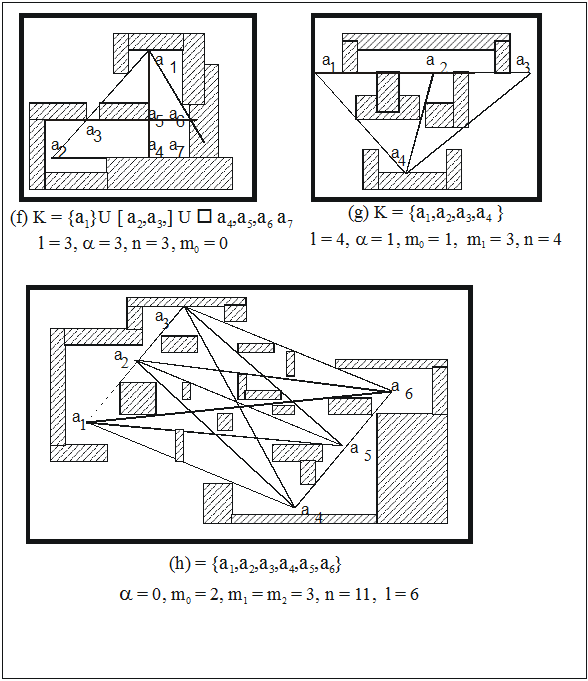
Рис. 7. (f, g, h) - иллюстрация характеристик несвязного класса:

l - число связных компонент, n - число "образующих" классов,

a - число "одиночных" компонент, m_i - число компонент в i-ом "пучке"

Теорема. Базис классов видимости имеет мощность континуум для любого террайна.

Доказательство теоремы приведено в [14].

Таким образом, поскольку базис классов видимости для эффективного графа районов не подходит, попытаемся организовать стандартное конечное покрытие террайна классами видимости.

Для построения конечного покрытия террайна, препятствия на котором - выпуклые, с углами 90° и 270°, классами видимости авторами был разработан следующий алгоритм:

1) Выбирается отрезок - произвольная сторона любого препятствия на террайне и максимально распространяется в обе стороны до пересечения с другими препятствиями. Полученный отрезок назовем фронтом видимости.

2) Фронт видимости распространяем в перпендикулярном к выбранной стороне препятствия направлении до прерывания его каким-либо препятствием. Полученная прямоугольная область очевидно будет классом видимости.

3) Повторяем шаги 1,2 для каждой стороны каждого препятствия. Получим совокупность пересекающихся классов видимости.

Поскольку работа первых трех шагов алгоритма не гарантирует покрытия всего террайна (например, на террайне типа «мельница», представленном на рис. 8), то проводим следующую процедуру

4) Выявляем непокрытую прямоугольную область террайна.

5) Для каждой стороны этой области строим фронт видимости и максимально распространяем его в соответствующем направлении. Полученная прямоугольная область также будет классом видимости

6) Повторяем шаги 4,5 для всех непокрытых областей террайна.

При таком построении возможно появление вложенных или идентичных классов видимости, поэтому имеет смысл проводить процедуру редукции числа классов, отслеживающую входящие друг в друга или равнозначные классы и удаляющую избыточные классы из построенного списка.

Результат работы алгоритма представлен на рис. 8. На рис. 9 изображен граф связей классов, полученный на основе результатов работы алгоритма. Вершинам графа соответствуют классы видимости, а ребрам – пересечения классов.

Теорема. Результат применения алгоритма построения покрытия классами видимости единственен (то есть не зависит от последовательности опорных отрезков).

Доказательство теоремы приведено в работе [15].

Указанное представление иллюстрирует рис. 8.

 

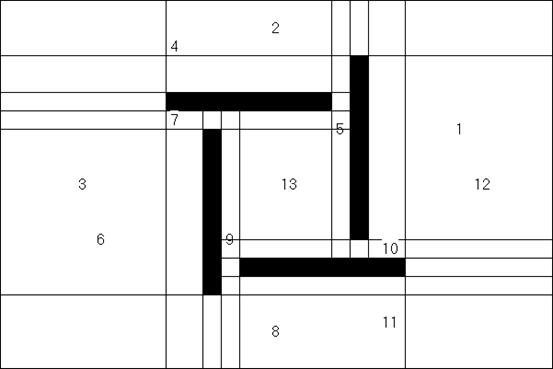
Рис. 8.

 

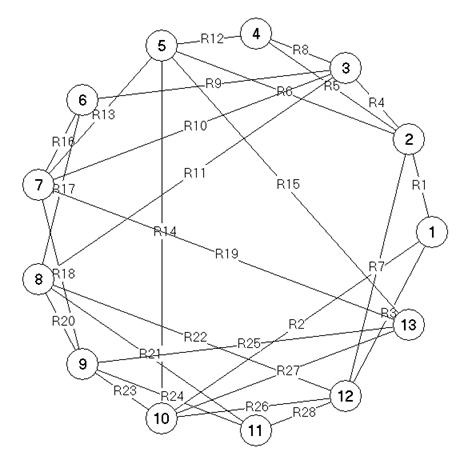
Рис. 9.

 

Возможные конфигурации сопряженного толерантного пространства иллюстрированы рис. 10-15. Следует отметить, что для рис. 10 не учтено влияние несвязных классов видимости.

 

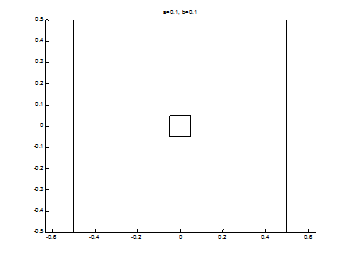Рис.10. Исходный террайн

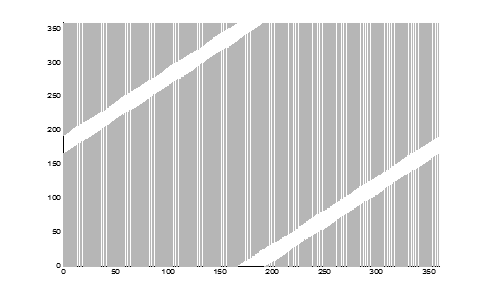
Рис. 11. Представление сопряженного пространства в декартовой СК

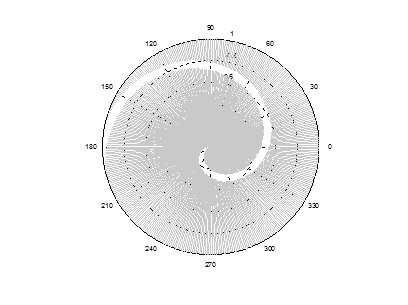
Рис. 12. Представление сопряженного пространства в полярной СК

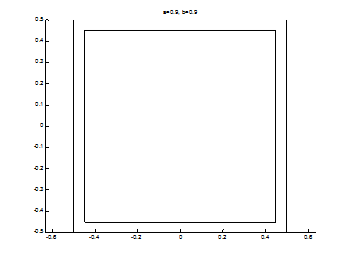
Рис.13. Исходный террайн

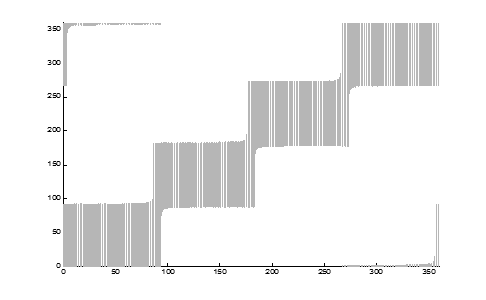
Рис. 14. Представление сопряженного пространства в декартовой СК

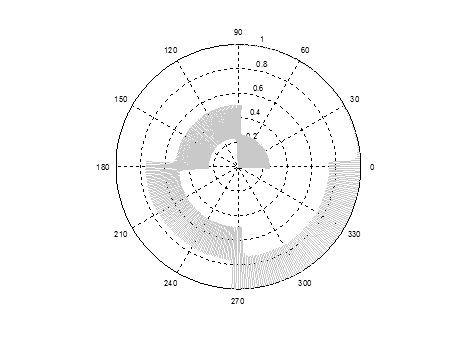
Рис. 15. Представление сопряженного пространства в полярной СК

 

Если А – навигационное множество и А(х) – навигационное описание, то для него можно определить понятие непрерывности. Это понятие и атлас особых ситуаций приведены на рис. 16.

Навигационное описание A(x) на основе навигационного множества A (V(A)=V), называется

(1) e - непрерывным, если (||x - y|| < e Þ(A(x)ÇA(y)¹Æ)

(2) непрерывным по отношению видимости, если ( x ~ y Þ(A(x)ÇA(y)¹Æ)

 

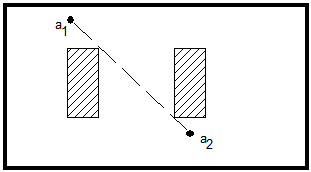
(а) Навигационное описание A(x) на основе навигационного множества A

={a₁,a₂} не является ни e-непрерывным, ни непрерывным по отношению

видимости.

 

 

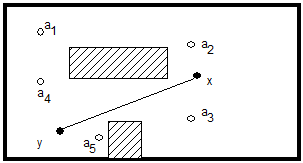
(б) Навигационное описание, продуцируемое множеством A={a _i},i =1, ...,5,

является e-непрерывным, но не является непрерывным по отношению

видимости.

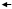
(в) Навигационное описание, продуцируемое множеством A={a _i}, i = 1,...,7, является непрерывным по отношению видимости, но не является e-непрерывным.

 

Рис. 16. Атлас для особых навигационных множеств

 

Нетрудно показать, что навигационное множество и исходный террайн толеоморфны.

 

Заключение

Приведённые результаты иллюстрируют использование теории толерантных пространств в различных областях: представление нейронной сети у Зимана и Бьюнемана, толерантных автоматов у Арбиба и, наконец, использование теории толерантных пространств для управления мобильными роботами и РМС. Последнее направление представляется наиболее перспективным.

 

ЛИТЕРАТУРА

1. Zeeman E.C. The topology of the brain and visual perception in: Topology of 3 manifolds, K. Fort ed., Preutice Hall, 1962, pp. 240-256.

2. Зиман Э., Бьюнеман О. Толерантные пространства и мозг. // На пути к теоретической биологии. I. Пролегомены. М.: Мир, 1970, с. 134-144.

3. Пуанкаре А. О науке. // М.: Наука, 1999, 736 с.

4. Секей Г. Парадоксы в теории вероятностей и математической статистике. // М.:Мир, 1990,240 с.

5. Калман Р., Фалб П., Арбиб М. Очерки по математической теории систем. // М.:Мир, 1971,400 с.

6. Богомолов А.М. Салий В.Н. Алгебраические основы теории дискретных систем. //Москва Наука – ФизМатЛит 1997,368 стр.

7. Ю. А. Шрейдер Равенство, Сходство, Порядок. //Москва Наука 1974, 254 стр.

8. Шрейдер Ю.А.. Пространства толерантности. // Кибернетика, №2 1970 стр. 124-128.

9. Якубович С.М.. О свойствах сопряжённости толерантных пространств. // Информ. Вопр. семиотики, лингвистики и автоматического перевода, 1971, вып. 1, стр. 116-122.

10. Sossinskiy A.B. Tolerance space theory and some applications. // Acta Applicandae Mathematicae // 1986, v.5, p.137-167.

11. Келдыш Л.В. Преобразование монотонного неприводимого отображения в монотонное открытое и монотонно-открытые отображения куба, повышающие размерность.// Матем. Сб., 1957, т.43, №2, с.187-226.

12. Келдыш Л.В. Некоторые вопросы топологии евклидовых пространств. // Усп. Матем. Наук, 1961, т.16, №1, с.3-18.

13. Кирильченко А.А. О представлении информационно-двигательного взаимодействия мобильного робота со средой на основе отношения видимости //М.: Препринт Ин-та прикл. матем. им. М.В.Келдыша АН СССР, 1987, N 235, 28 с.

14. Кирильченко А.А. Ядра и классы видимости в задачах информационного обеспечения мобильных роботов //Москва Препринт ин-та прикл. Матем. Им. М.В. Келдыша АН СССР, 1988, №181, 28с.

15. Барбашова Т.Ф., Кирильченко А.А., Колганов М.А. Некоторые аспекты использования метода потенциалов при управлении мобильными роботами. //Препринт Ин-та прикл. матем. им.М.В.Келдыша РАН, 2004, N 21, 26 с.