 |
Главная |
Основы теоретической робототехники. Теория толерантных пространств (обзор).
|
из
5.00
|
Москва, 2009 г.
Александрова А.А., Ахтеров А.В., Воронин А.Ю., Кирильченко А.А., Соколов С.М., Швайковский Е.В.
ОСНОВЫ ТЕОРЕТИЧЕСКОЙ РОБОТОТЕХНИКИ. ТЕОРИЯ ТОЛЕРАНТНЫХ ПРОСТРАНСТВ (ОБЗОР).
Alexandrova A.A., Akhterov A.V., Voronin A.Yu., Kirilchenko A.A., Sokolov S.M., Shvaikovskiy E.V.
BASICS OF THEORETICAL ROBOTECHNICS. TOLERANT SPACES THEORY (REVIEW).
АННОТАЦИЯ
В работе рассматриваются основы теории толерантных пространств, изложенные в работах Э. Зимана, М. Арбиба, Ю. Шрейдера, А. Соссинского. Следует отметить, что основные отношения в задаче выбора пути для роботов – отношение достижимости и отношение видимости – являются отношениями толерантности. В работе изложены основы теории террайнов – метрических толерантных пространств для решения задач выбора пути и сопутствующей навигации.
ABSTRACT
This work highlights of basics of tolerance space theory, which was proposed by E.Ziman, M. Arbib, Yu. Shraider and A. Sossinsky. The basic relations in the task of path finding problem for mobile robots is visibility relation (tolerance relation). This work is highlighted the basics of terrain theory (metric tolerance spaces) for path finding and navigation problems.
Работа частично поддерживалась грантом РФФИ 08-01-00908
СОДЕРЖАНИЕ
Введение............................................................................................................. 3
Линия Э. Зимана................................................................................................ 3
Линия М. Арбиба. Толерантные автоматы...................................................... 5
Линия Ю. Шрейдера......................................................................................... 7
Линия А. Сосинского. Толеоморфизмы........................................................... 11
Теория Террайнов............................................................................................. 12
Заключение........................................................................................................ 24
Литература........................................................................................................ 25
ВВЕДЕНИЕ
Отношение толерантности есть отношение рефлексивное и симметричное, но в общем случае не транзитивное. В настоящее время отношение толерантности обычно упоминается в алгебраических основах теории дискретных систем [6].
Впервые отношение толерантности было введено Э. Зиманом в 1963 году как аналог дифференциального порога в психологии. В связи с этим можно упомянуть идею Пуанкаре о физическом равенстве (А=В, В=С, А¹С) [3].
В работе рассмотрены основные источники по теории толерантных пространств.
Изложены основы теории террайнов (метрических толерантных пространств) на основе карт среды.
1. ЛИНИЯ Э. ЗИМАНА
Первый шаг в этой истории сделал Э. Зиман в своей работе [1]. Наиболее подробно этот подход освещен в [2]. Понятие толерантности принимается как соответствующее «наименьшему воспринимаемому различию» (дифференциальному порогу) в психологии. Если два раздражения х и у настолько близки, что не поддаются различению, то это означает, что они связаны отношением толерантности (находятся в пределах толерантности) [2, c. 134].
Толерантное пространство есть пара <М, t >, где М - множество-носитель, t - отношение толерантности.
Всем работам по толерантным пространствам свойственны обширные рассуждения в области прикладной философии этой математической структуры. Эти рассуждения имеют не только исторический интерес.
Согласно [2], в основе математической теории толерантных пространств (МТТП) лежат два свойства отношения толерантности.
1. В пределах толерантности можно перемещаться, не замечая различий. Например, совпадение двух объектов может быть проверено в пределах толерантности, также как и исследование структурной устойчивости некоторого дифференциального уравнения.
2. Толерантность, подобно топологии, вносит некоторое понятие близости элементов, причем нетранзитивное.
В [2] утверждается, что ТП напоминает «размазанное» (в соответствии с теорией «мягких вычислений», сегодня можно сказать «размытое») топологическое пространство в том смысле, что в МТТП в перспективе могут эффективно использоваться глобальные инварианты, а локальными свойствами можно пренебречь.
Указанные два свойства, в общем-то, представляют две стороны одной медали. Предпосылки к важности подобного понимания толерантности могут быть найдены в истории математики. Здесь имеет смысл остановиться на следующих двух фактах.
Во-первых, это рассуждения Анри Пуанкаре о «физической непрерывности» [3, с. 27-28]. Обсуждая вопрос об ощущениях человека, автор выводит типичную формулу физической непрерывности:
А=В=С, при этом А<С.
Эта формула выражает то, что А и В неразличимы человеком (например, по весу), также как и В и С, однако А и С человеком различаются.
Во-вторых, можно упомянуть парадокс равенства математических ожиданий [4, с. 126-127]. Пусть математические ожидания трех нормально распределенных случайных величин с одинаковыми дисперсиями равны M 1 , М2 и М3. Тогда может случиться так, что используя распределение Стьюдента, можно принять гипотезы M 1 = М2 и М2 = М3 и М1 ¹ М3; таким образом, речь идёт о нетранзитивности равенства, которое представляет собой отношение толерантности.
Здесь имеет смысл упомянуть следующие оригинальные определения «отца» отношения толерантности [2].
1. Примеры толерантных пространств (ТП). Отношение толерантности обозначается ‘~’.
Пример А. Если ( X , т) - ТП, то в булеане (множестве всех подмножеств) можно ввести толерантность 2х, положив, что А ~ В в 2X в смысле ~T,если " x Î A $ y Î B: х ~ у в смысле T, и обратно. Это позволяет перейти от толерантности в множестве точек поля зрения к толерантности в множестве черно-белых изображений.
Пример Б. Пусть ( X , x ) и ( Y , h ) - два ТП и Y X - совокупность всех отображений X в Y . Тогда толерантность h xозначает f ~ g , если графики этих отображений в X ´ Y толерантны между собой в смысле толерантности h ´ x . Это построение позволяет перейти от ТП ( X , x ) полей зрения и ТП ( Y , h ) цветов к ТП (Yх, hx) цветных изображений.
Пример В. Пусть X - множество двумерных проекций среды (местности, трехмерного мира), а x - толерантность, определяемая небольшими параллактическими движениями головы человека. Утверждалось, что это именно та геометрическая структура, которая «используется» в зрительном анализаторе человека.
2. Толерантное отображение и толерантный гомеоморфизм
Именно эти типы соответствий приняты в [2] за базовые.
Если ( X , x ) и ( Y , h ) суть ТП и ¦: X ® Y отображение, то ¦ называется толерантным, если из x 1 ~ x 2 в смысле x следует ¦x1~¦x2 в смысле h . Если справедливо и обратное, то ¦ называют толерантным вложением. Если при этом "yÎY $xÎX (y~¦x), то ¦ называют толерантным гомеоморфизмом. Композиция двух толерантных отображений или вложений будет отображением того же типа, однако композиция двух толерантных гомеоморфизмов в общем случае гомеоморфизмом не будет. Этот момент аналогичен тому, что в общем случае отношение и композиция отношений транзитивными быть не обязаны.
Ниже приведен пример.
| ¦ | g | |||
| (X,x) | ® | (Y,h) | ® | (Z,y) |
Здесь y1 = f ( x ); z 1 = g ( y 1 ); y 2 ~ y 1 , но у2 не принадлежит образу f ( x ). Однако у2 ~ y 1 и z3 ~ z 2 . Теперь, если рассмотреть композицию gf , то «ближайшей» точкой из gf ( x ) к z3 будет z1, но z 3 ~ z 2 в смысле y 2.
Дальнейшая программа исследований была сформулирована следующим образом [2, с. 143-144]: «если дано ТП (Х, x ), то мы можем построить симплициальный комплекс, состоящий из всех симплексов, где симплекс - это такое конечное ориентированное подмножество множества X , все точки которого толерантны между собой. Группой гомологии H ( X , x ) будет тогда по определению группа гомологии этого комплекса. Хотелось бы иметь следующую теорему:
Теорема: толерантный гомеоморфизм индуцирует изоморфизмы соответствующих групп гомологии.
Однако, это не вполне верно; необходимо сделать некоторые технические уточнения. Все же из правильной формулировки этой теоремы можно сделать вывод о том, что такие свойства, как связность, число дыр и размерность, сохраняются при толерантном гомеоморфизме».
Все это направление предполагалось использовать для «пионерского» описания работы мозга на основе псевдодифференциально-толерантных уравнений. Что из всего этого получилось - авторам неизвестно (публикации по МТТП очень редки и труднодоступны).
2. ЛИНИЯ М. АРБИБА. ТОЛЕРАНТНЫЕ АВТОМАТЫ.
«Каждый раз, когда речь заходит об использовании непрерывности, специалист по теории автоматов начинает испытывать острую зависть к специалисту по теории управления. В связи с этим возникает следующая задача: как определить содержательную топологию на дискретном множестве, отличную от дискретной топологии?... Каково должно быть определение непрерывности, чтобы она естественно присутствовала в поведении конечных автоматов?»
В ответ на эти вопросы М. Арбиб [4] предложил идею толерантных автоматов. В её основе – попытка определения понятия непрерывности в пространстве состояний. [4, c. 204].
Серия определений и утверждений М. Арбиба [4].
1. Пусть М=(X,Y,Q,l,d) есть автомат, (Q,x) – толерантное пространство.
Автомат М называется толерантным, если ("xÎX)("qÎQ)((q,l(q,x))ÎxQ).
Таким образом, толерантные автоматы обладают инерцией; неожиданное изменение входного воздействия не может вызвать резкого изменения состояния автомата.
2. Функция f: X->Y между двумя толерантными пространствами называется n-непрерывной, если ((x1,x2)ÎxX ) => ((f(x1),f(x2))ÎxY).
3. Пространство С называется платёжным, если
а) (С,x) есть толерантное пространство;
в) С есть абелева группа с групповой операцией, обозначаемый символом «+», частично упорядочиваемой отношением £.
с) ("сÎС)($аÎС)($bÎС): (а<c<b)Ù(a<c’<b) ó((c,c’)Îx)
4. Платёжной функцией автомата М=(X,Y,Q,l,d) и заданного платёжного пространства С называют некоторую функцию p: Q´X->C. Если продолжить Р на множество Q´X*, потребовав, чтобы р(q,xÇy)=p(q,x)+p(l(q,x),y), то задачу оптимального управления автоматом можно сформулировать следующим образом.
5. Задача оптимального управления.Пусть q0 и q1 есть два состояния из Q, называемые соответственно начальным и конечным. При этом u=((u1,…,un)ÎX*) переводит М из состояния q0 в состояние q1, если l(q0,u)=q1 и в то же время l(q0,u1..uk)¹q1 при всех k<n. Требуется среди всех последовательностей u из Х*, переводящих М из q0 в q найти такую, для которой Р(q0,y) минимально.
6. Пусть M=(X, Y, Q, l, d) есть некоторый автомат с платежной функцией p и платежным пространством С. Определим тогда автомат
(M, p) = (X, Y, Q×C, lp,dp)
следующим образом:
lp(q, c, x)=(l(q, x), c + p(q, x)),
dp(q, c, x)=d(q, x)
7. Пусть достижимым в Q × C × T множеством Rq0 называется
{(lp(q0, 0, u), l(u)): u Î X*},
где lp(q0, 0, L) = (q0, 0), а L есть пустая последовательность.
8. Для каждого n рассмотрим сечение множества Rq 0 в момент времени n :
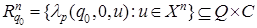
Если последовательность u оптимальна, то ей соответствует минимальная проекция на C по сравнению с любыми другими точками сечения 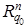 , и, следовательно, необходимое условие оптимальности управления u состоит в том, чтобы lp(q0, 0, u) определяло точку на границе множества Rq0.
, и, следовательно, необходимое условие оптимальности управления u состоит в том, чтобы lp(q0, 0, u) определяло точку на границе множества Rq0.
9. Справедлива следующая теорема. Для каждого состояния q 1-толерантного автомата M и каждого n Î T множество 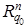 связно относительно
связно относительно 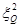 .
.
10. Пусть S есть некоторое подмножество толерантного пространства X. Тогда назовём
x -замыканием подмножества S множество 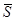 = {x: (x,y)Îx} для некоторого xÎS
= {x: (x,y)Îx} для некоторого xÎS
x -внутренностью подмножества S множество int S ={x: (x, y)ÎxÞy Î S};
x -границей подмножества S множество dS = 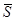 \ int S = {x: (x , y)Îx для некоторого yÎS, но (x , z)Îx для некоторого z Ï S.
\ int S = {x: (x , y)Îx для некоторого yÎS, но (x , z)Îx для некоторого z Ï S.
11. Справедлива лемма: X \ 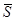 = int (X \ S)
= int (X \ S)
12. Справедлива теорема:
Пусть M есть 1-толерантный автомат, и пусть u = ( u 1 ,…, un ) Î Xn . Если
l p ( q , u ) Î 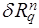 , то
, то
( qk , ck ) = l p ( q , 0, u 1 , … , uk ) Î 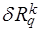 , 1£k£n
, 1£k£n
В этой теореме легко узнать аналог теоремы, на которой базируется принцип максимума Понтрягина в теории оптимальных систем.
3. ЛИНИЯ Ю.А.ШРЕЙДЕРА [7,8]
Ядро толерантности есть множество точек, множество толерантных к которым элементов есть постоянное множество. Класс толерантности есть аналог клики на графе. Порожденная классами толерантность в пространстве классов определяется так: два элемента сопряженного пространства классов толерантны порожденной толерантностью, если соответствующие им классы имеют непустое пересечение. Классы порожденной толерантности называются каноническими признаками. Базис классов толерантности определяется следующим образом. Если х толерантно y, то существует класс толерантности, содержащий оба этих класса, и нельзя из базиса удалить какой-либо класс толерантности без потери первого свойства.
Классы образуют сопряженное к исходному пространство. Два класса считаются толерантными, если их пересечение – непустое множество. Сопряженное к сопряженному пространство вкладывается в исходное толерантное пространство [7,9].
Проиллюстрируем сказанное следующим примером. Возьмём граф, в котором все циклы строятся на основе клик. Нетрудно видеть, что любой неориентированный граф представляет собой толерантное пространство. Проводя итерационно переходы к сопряжённому пространству к данному графу (сопряжённое пространство, сопряжённое к сопряжённому и т.п.), в конце концов мы получим одну вершину. Это справедливо только для графов указанного типа. Нетрудно видеть, простой цикл размерностью больше 3 при сопряжённом преобразовании сохраняется. Приведённое выше утверждение имеет сложное доказательство, и мы поясним его следующим примером - см. рис.1, а-е.
Легко заметить, что через 7 итераций граф сойдётся в точку. На рисунках указан диаметр графа g и число доминирования nmin.
ИСХОДНЫЙ ГРАФ. g=5 nmin=4
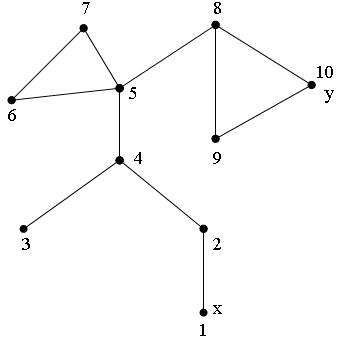
Рис. 1а
I итерация.
g=5 nmin=3
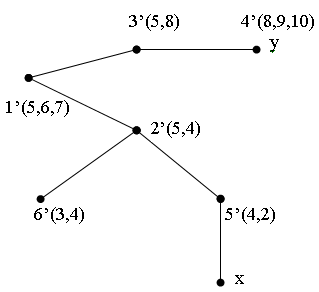
Рис. 1б
II итерация.
g=4 nmin=3
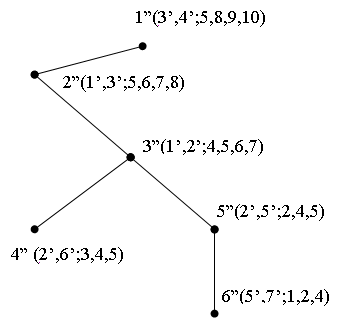
Рис. 1в
III итерация.
g=3 nmin=2
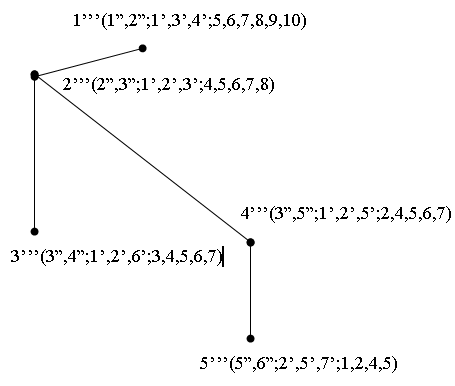
Рис. 1г
IV итерация.
g=3 nmin=2

Рис. 1д
V итерация.
g=2 n=1
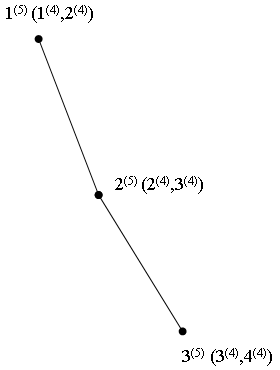
Рис. 1е
Очевидно, что толерантное пространство легко можно превратить в топологическое пространство, поскольку это есть пространство метрическое. Целочисленная метрика между двумя точками есть минимальное число звеньев у допустимой ломаной, которая их соединяет.
4. ЛИНИЯ А. СОСИНСКОГО. ТОЛЕОМОРФИЗМЫ.
В основополагающей статье А.Б. Сосинского [10] нас прежде всего интересует понятие толеоморфизма. Толеоморфизм – отношение похожести толерантных пространств, в отличие от изоморфизма линейных пространств и графов. На основе толеоморфизма можно определить отношение толерантности между ТП [10].
Определение. Xx и Yh называют толеоморфными, если существуют два морфизма 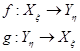 , которые:
, которые:
а) почти инъективны:
"x, x’ÎX f(x)=f(x’) -> x2xx’
"y, y’ÎY g(y)=g(y’) -> y2hy’
б) почти сюръективны:
"yÎY 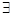 xÎX f(x)hy
xÎX f(x)hy
"xÎX 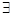 yÎY g(y)xx
yÎY g(y)xx
в) почти обратимы:
"xÎX 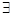 yÎY f(x)hy g(y)2x(x)
yÎY f(x)hy g(y)2x(x)
"yÎY 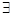 xÎX g(y)xx f(x)2h(y)
xÎX g(y)xx f(x)2h(y)
(f,g) – толеоморфизм. (f,g) 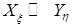 : Xx
: Xx 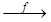 Yh , Yh
Yh , Yh 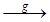 Xx
Xx
На рис. 2 приведён пример двух неизоморфных, но толеоморфных пространств.
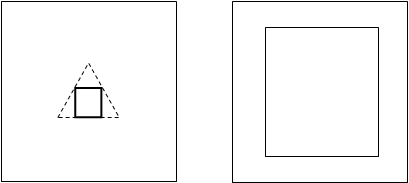
Рис. 2.Пример “2-Швайковский-2“
Теорема Л.В.Келдыш [11,12] говорит о существовании непрерывного отображения трёхмерного куба на четырёхмерный. А. Б. Сосинский предлагает использовать для кодирования не само открытое монотонное отображение Келдыш, а вложение Келдыш трёхмерного куба в четырёхмерный. Это вложение возникает в промежуточном рассуждении при построении самого отображения. Это вложение является толеоморфизмом.
В [10] показано, что отношение толеоморфизма есть отношение толерантности между толерантными пространствами.
5. ТЕОРИЯ ТЕРРАЙНОВ.
Движение РМС задается в террайне – ограниченной прямоугольной рамкой области с препятствиями, непрозрачными для измерителя и непреодолимыми для МР. Для простоты препятствия представляют собой многоугольники с углами в вершинах в 90° и 270°. Подобные модели активно исследовались в ИПМ им.М.В.Келдыша РАН [4,5] и других исследовательских организациях. Пример террайна изображён на рис. 3.
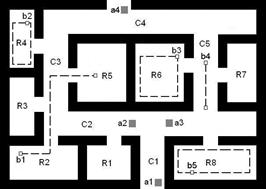
Рис. 3. Пример террайна. R1…R8 – комнаты; а1…а4 – элементы РМС; b1…b5 – неизвестные объекты. Пунктиром показаны возможные перемещения неизвестных объектов
Две точки x,y видимы одна из другой (что записывается как x~y), если отрезок [x,y] не пересекает препятствий (но может их касаться).
В общем случае террайн Ter = < V , r , a , ~, [...]>, где
V - носитель террайна,
r ( x , y ) - исходная евклидова метрика,
a ( x , y ) - вторая основная непрерывная метрика, удовлетворяющая отношению a ( x , y ) ³ r ( x , y ), т.е. длина кратчайшего пути, не пересекающего препятствий),
“~” - основное отношение толерантности (отношение видимости), которое может быть определено по схеме (x~y) <=>(a ( x , y )= r ( x , y )),
[...] - индуцированные на основе указанных выше метрик и толерантности другие метрики и толерантности [4].
Всегда предполагается, что число препятствий в террайне и число вершин препятствий конечны.
Отрезок 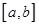 называется касательным, если: 1) он максимален для данного террайна, т.е. в направлении из
называется касательным, если: 1) он максимален для данного террайна, т.е. в направлении из 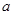 в
в 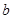
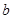 является максимально удалённой видимой из
является максимально удалённой видимой из 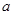 точкой и наоборот; 2) на интервале
точкой и наоборот; 2) на интервале 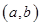 есть как граничные точки, так и внутренние точки террайна. Отрезок
есть как граничные точки, так и внутренние точки террайна. Отрезок 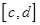 называется выходным, если: 1)
называется выходным, если: 1) 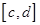 строго входит в некоторый касательный отрезок; 2)
строго входит в некоторый касательный отрезок; 2) 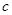 и
и 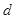 являются граничными точками террайна; 3) интервал
являются граничными точками террайна; 3) интервал 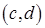 состоит только из внутренних точек террайна. Если выходной отрезок
состоит только из внутренних точек террайна. Если выходной отрезок 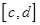 строго входит в касательный отрезок
строго входит в касательный отрезок 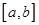 , а точка
, а точка 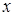 расположена на этом касательном отрезке и не принадлежит указанному выходному отрезку,
расположена на этом касательном отрезке и не принадлежит указанному выходному отрезку, 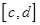 называется наблюдаемым в точке
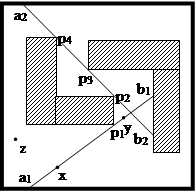
называется наблюдаемым в точке 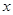 выходным отрезком. Вершины препятствий, расположенные на интервале касательного отрезка, называются замыкающими вершинами. Ориентация замыкающей вершины определяется тем, по какую сторону от касательного отрезка расположены содержащие замыкающую вершину граничные отрезки препятствий. Сказанное иллюстрирует рис.4.
выходным отрезком. Вершины препятствий, расположенные на интервале касательного отрезка, называются замыкающими вершинами. Ориентация замыкающей вершины определяется тем, по какую сторону от касательного отрезка расположены содержащие замыкающую вершину граничные отрезки препятствий. Сказанное иллюстрирует рис.4.
|
Рис. 4 Отрезки 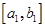 и и 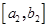 являются касательными отрезками; являются касательными отрезками; 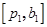 - выходной отрезок, наблюдаемый в точке - выходной отрезок, наблюдаемый в точке 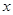 ; ; 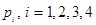 - замыкающие вершины на указанных касательных отрезках. - замыкающие вершины на указанных касательных отрезках.
|
Наряду с традиционным понятием границы множества M в террайнах большую роль играет свободная граница множества M - dM. Она определяется как подмножество таких точек x "обычной границы", что в сколь угодно малой окрестности x найдутся точки y из носителя террайна V, которые не входят в замыкание M.
Отличие от "обычной границы" в том, что там все точки y, не входящие в замыкание M, могут принадлежать препятствию. dV(x) - множество, через которое МР может покинуть V(x) – видимую окрестность x (т.е. множество всех точек, видимых из x). Видимая окрестность множества V(M) понимается как объединение видимых окрестностей всех точек множества.
Нетрудно видеть, что V(M) = V(dM).
Ядра и классы видимости являются основными структурными образованиями на террайне [13,14]. Напомним, что отношение видимости есть отношение толерантности, так что классы и ядра видимости являются примером классов и ядер толерантности.
Ядром видимости называется максимальная область, для каждой точки которой видимая окрестность одна и та же.
Утверждение.
Если в любой точке террайна наблюдаются два выходных отрезка, которые входят в разные касательные отрезки, т.е. неколлинеарны, то в таком террайне отсутствуют нетривиальные (т.е. состоящие более чем из одной точки) ядра видимости.
Утверждение следует из теоремы, доказанной в [14], о представлении ядер видимости. Атлас возможных типов ядер видимости представлен на рис.5. Здесь изображены:
(5a): "Веер" ядер у вершины p. Каждое ядро – полуинтервал, одно из граничных точек террайна (второго типа), остальные из внутренних точек террайна (первого типа), с граничной точкой террайна– концом полуинтервала.
(5b): Ядро первого типа – интервал.
(5c): Усеченное ядро первого типа – отрезок – с граничной точкой террайна – одним из концов отрезка.
(5d): В данной ситуации ядра не наблюдается.
(5e): Невырожденное ядро второго типа, состоящее из одного или нескольких интервалов (случай несвязного ядра) граничных точек террайна.
(5f): Усеченное ядро второго типа, представляющее собой отрезок, входящий в состав граничного отрезка террайна.
(5g): Разбиение ядра второго типа из-за ситуации типа "двойной замок".
(5h): Ситуация типа "цепь": между компонентами несвязного ядра второго типа находятся ядра первого типа.
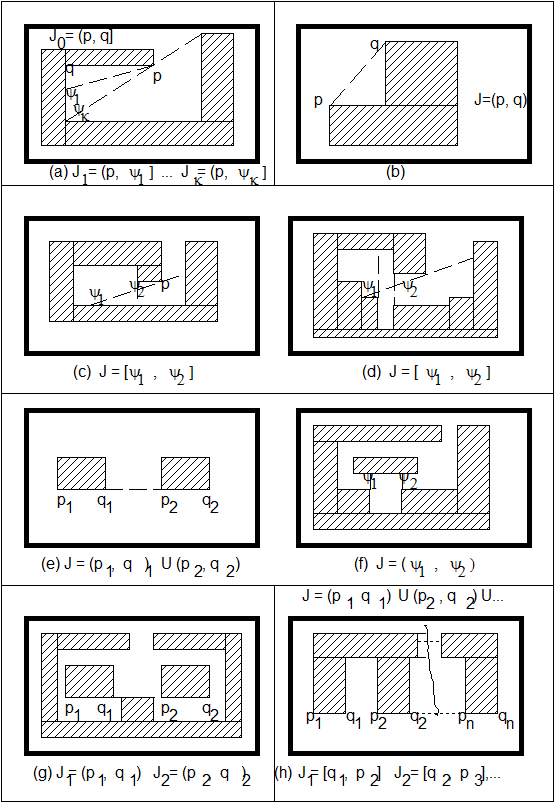
Рис. 5. Атлас ядер
Классом видимости называется максимальная область, все точки которой видимы одна из другой. Это понятие, также как и понятие класса толерантности в общем случае [7, 8], является аналогом понятия клики на конечном графе.
Класс видимости может быть связным или несвязным множеством. Нетрудно видеть, что несвязный класс видимости может быть гомоморфно отображен на полный граф.
Справедливы следующие теоремы.
|
из
5.00
|
Обсуждение в статье: Основы теоретической робототехники. Теория толерантных пространств (обзор). |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

