Двойственность в линейном программировании

КУРСОВАЯ

на тему:

 

 

Двойственный симплекс-метод и доказательство теоремы двойственности.

 

 

Студент группы МЭК 1-1   - А.С. Кормаков

Научный руководитель           - Солодовников А.С.

 

МОСКВА – 2001

 

Содержание

1. Двойственность в линейном программировании.................................... 3

2. Несимметричные двойственные задачи. Теорема двойственности... 4

3. Симметричные двойственные задачи........................................................ 9

4. Виды математических моделей двойственных задач........................... 11

5. Двойственный симплексный метод........................................................... 12

6. Список используемой литературы............................................................ 14

 

 

Двойственность в линейном программировании

Понятие двойственности. С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется исходной.

Связь исходной и двойственной задач состоит в том, что коэффици­енты C_j  функции цели исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные члены B_i систе­мы ограничений исходной задачи служат коэффициентами функции цели двойственной задачи, а матрица коэффициентов системы ограни­чений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи. Решение двой­ственной задачи может быть получено из решения исходной и наоборот.

В качестве примера рассмотрим задачу использования ресурсов. Предприятие имеет т видов ресурсов в количестве b_i (i = 1, 2, ..., m) единиц, из которых производится n видов продукций. Для производ­ства 1 ед. i-й продукции расходуется a_ij ед. t-гo ресурса, а ее стоимость составляет C_j ед. Составить план выпуска продукции, обеспечивающий ее максимальный выпуск в стоимостном выражении. Обозначим через x_j(j =1,2, ..., n) количество ед. j-й продукций, Тогда исходную задачу сформулируем так.

Найти вектор Х =(x₁, x₂, …, x_n), который удовлетворяет ограни­чениям

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n £ b_1,

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n £ b_2,                  x_j ³ 0 (j =1,2, ..., n)

…………………………………

a_m1x₁ + a_m2x₂ + … + a_mnx_n £ b_m,

 

и доставляет максимальное значение линейной функции

Z = C₁x₁ + C₂x₂ + … + C_nx_n,

Оценим ресурсы, необходимые для изготовления продукции. За единицу стоимости ресурсов примем единицу стоимости выпускаемой продукции. Обозначим через у _i (j =1,2, ..., m) стоимость единицы i-горесурса. Тогда стоимость всех затраченных ресурсов, идущих на изготовление единицы j-й продукции, равна 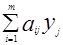. Стоимость затрачен­ных ресурсов не может быть меньше стоимости окончательного продукта, поэтому должно выполняться неравенство 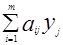³ C_j, j =1,2, ..., n. Стоимость всех имеющихся ресурсов выразится величиной 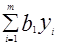. Итак, двойственную задачу можно сформулировать следующим образом.

Найти вектор Y =(y₁, y₂, …, y_n), который удовлетворяет ограни­чениям

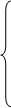a₁₁y₁ + a₁₂y₂ + … + a_m1y_m £ C_1,

a₁₂y₁ + a₂₂y₂ + … + a_m2y_m £ C_2,                  y_j ³ 0 (i =1,2, ..., m)

…………………………………

a_1ny₁ + a_2ny₂ + … + a_mny_m £ C_m,

и доставляет минимальное значение линейной функции

f  = b₁y₁ + b₂y₂ + … + b_my_m.

Рассмотренные исходная и двойственная задачи могут быть эко­номически интерпретированы следующим образом.

Исходная задача. Сколько и. какой продукции x_j (j =1,2, ..., n) необходимо произвести, чтобы при заданных стоимостях C_j (j =1,2, ..., n) единицы продукции и размерах имеющихся ресурсов b_i (i =1,2, ..., n) максимизировать выпуск продукции в стоимостном выражении.

Д в о й с т в е н н а я  з а д а ч а. Какова должна быть цена еди­ницы каждого из ресурсов, чтобы при заданных количествах ресурсов b _i и величинах стоимости единицы продукции C _i минимизироватьобщую стоимость затрат?

Переменные у _i называются оценками или учетными, неявными ценами.

Многие задачи линейного программирования первоначально ста­вятся в виде исходных или двойственных задач, поэтому имеет смысл говорить о паре двойственных задач линейного программирования.

 2. Несимметричные двойственные задачи. Теорема двойственности.

В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной — в виде нера­венств, причем в последней переменные могутбыть и отрицательными.Для простоты доказательств постановку задачи условимсязаписывать в матричной форме.

Исходная задача. Найти матрицу-столбец X = (x₁, x₂, …, x_n), которая удовлетворяет ограничениям

(1.1)                   AX = A₀, Х ³ 0

и минимизирует линейную функцию Z = СХ.

Двойственная задача. Найти матрицу-строку Y = (y₁, y₂, …, y_m), которая удовлетворяет ограничениям

(1.2)                    YA £ С

и максимизирует линейную функцию f = YA₀

В обеих задачах C = (c₁, c₂, …, c_n) - матрица-строка, A₀ = (b₁, b₂, …, b_m) — матрица-столбец, А = (a_ij) — матрица коэффициентов системы ограничений. Связь между оптимальными планами пары двой­ственных задач устанавливает следующая теорема.

Теорема (теорема двойственности). Если из пары двойствен­ных задач одна обладает оптимальным планом, то и другая имеет ре­шение, причем для экстремальных значений линейных функций выпол­няется соотношение

min Z = max f.

Если линейная функция одной из задач не ограничена, то другая не имеет решения.

Д о к а з а т е л ь с т в о. Предположим, что исходная задача об­ладает оптимальным планом, который получен симплексным методом. Не нарушая общности, можно считать, что окончательный базис со­стоит из т первых векторов A₁, A₂, ..., A_m. Тогда последняя симплекс­ная таблица имеет вид табл. 1.1.

Т а б л и ц а 1.1

 

i	Базис	С базиса	A0	C1	C2	…	Cm	Cm+1	…	cn
				A1	A2	…	Am	Am+1	…	An
1 2 . . . m	A1 A2 . . . Am	C1 C2 . . . Cm	x1 x2 . . . xm	1 0 . . . 0	0 1 . . . 0	... ... . . . .	0 0 . . . 1	x1, m+1 x2, m+1 . . . xm, m+1	… … . . . …	x1n x2n . . . xmn
m+1	Zi - Cj		Z0	Z1 – C1	Z2 – C2	...	Zm – Cm	Zm+1 – Cm+1	…	Zn – Cn

 

Пусть D — матрица, составленная из компонент векторов оконча­тельного базиса A₁, A₂, ..., A_m; тогда табл. 1.1 состоит из коэффици­ентов разложения векторов A₁, A₂, ..., A_n исходной системы по векто­рам базиса, т. е. каждому вектору A_j в этой таблице соответствует та­кой вектор X_j что

(1.3)              A_j = DX_j (j= 1,2, ,.., n).

Для оптимального плана получаем

(1.4)                   A₀ = DX*,

где X* = ( x*₁ , x*₂ , …, x*_m ) .

Обозначим через 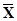 матрицу, составленную из коэффициентов раз­ложения векторов А _j (j = 1, 2, ..., n), записанных в табл. 1.1. Тогда, учитывая соотношения (1.3) и (1.4), получаем:

(1.5)                 A = D 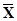,  D^-1A = ,

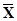(1.6)               A ₀ =DX*; D ^-1 A ₀ = X* ,

(1.7)                   min Z= C*X*,

(1.8) 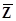                   = C* 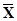—C £ 0,

где С* = (C*₁, C*₂, …, C*_m), С = (C₁, C₂, …, C_m, C_m+1, …, C_n), a 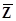 = (C*X₁ – C₁; С*Х ₂  - С₂, ..., C*X _n – C_n) = (Z₁ – С₁; Z₂  - C₂; ..., Z_n — C_n) — вектор, компоненты которого неположительны, так как они совпадают с Z_j — C_j  £ 0, соответствующими оптимальному плану.

Оптимальный план исходной задачи имеет вид X* = D^-1 А₀, поэтому оптимальный план двойственной задачи ищем в виде

(1.9)                           Y* = C*D ^-1 .

Покажем, что Y* действительно план двойственной задачи. Для этого ограничения (1.2) запишем в виде неравенства YA — С £ 0, в левую часть которого подставим Y*. Тогда на основании (1.9), (1.5) и (1.8) получим

Y * А – С = С* D ^-1 А – С = С* 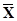 - С £ 0,

откуда находим Y*A £ С.

Так как Y* удовлетворяет ограничениям (1.2), то это и есть план двойственной задачи. При этом плане значение линейной функции двой­ственной задачи f (Y*) = Y*A ₀. Учитывая соотношения (1.9), (1.6) и (1.7), имеем

(1.10)                   f (Y*) = Y*A ₀ = C*D^-1 A₀ = C*X* = min Z(X).

Таким образом, значение линейной функции двойственной задачи от Y* численно равно минимальному значению линейной функции исходной задачи.

Докажем теперь, что Y* является оптимальным планом. Умножим (1.1) на любой план Y двойственной задачи, а (1.2) — на любой план X исходной задачи: YAX=YA ₀ = f ( Y), YAX £ СХ = Z (X), отсюда следует, что для любых планов Х и Y выполняется неравенство

(1.11)                    f ( Y) £ Z (X).

Этим же соотношением связаны и экстремальные значения max f ( Y) £  min Z (Х). Из последнего неравенства заключаем, что максималь­ное значение линейной функции достигается только в случае, если max f (Y) = min Z (X), но это значение [см. (1.10)] f ( Y) достигает при плане Y*, следовательно, план Y* — оптимальный план двойственной задачи.

Аналогично можно доказать, что если двойственная задача имеет решение, то исходная также обладает решением и имеет место соотно­шение max f (Y) = min Z (X).

Для доказательства второй части теоремы допустим, что линейная функция исходной задачи не ограничена снизу. Тогда из (1.11) следу­ет, что f (Y) £ -¥ . Это выражение лишено смысла, следовательно, двойственная задача не имеет решений.

Аналогично предположим, что линейная функция двойственной за­дачи не ограничена сверху. Тогда из (1.11) получаем, что Z (X) ³ +¥. Это выражение также лишено смысла, поэтому исходная задача не име­ет решений.

Доказанная теорема позволяет при решении одной из двойственных задач находить оптимальный план другой.

Исходная задача. Найти минимальное значение линейной функ­ции Z = x₂ – x₄ – 3x₅ при ограничениях

 

x₁ + 2x₂     - x₄ + x₅    = 1,

- 4x₂ + x₃ + 2x₄ – x₅    = 2,          x_ij ³ 0 (j = 1, 2, …, 6)

3x₂             + x₅ + x₆ = 5,

Здесь матрица-строка С = (0;. 1; 0; —1; — 3, 0), матрица-столбец

        1                             1 2 0 -1 1 0

A₀ = 2                A =  0 -4 1 2 -1 0

        3                             0 3 0 0 1 1

 

         1 0 0

         2 -4 3

A’’ =  0 1 0

        -1 2 0

         1 -1 0

         0 0 1

Двойственная задача. Найти максимальное значение линейной функции f = y₁ + 2y₂ +5y₃ при ограничениях

 y₁                £ 0,

2y₁ – 4y₂ + 3y₃ £ 1,

      y₂      £ 0,

-y₁ + 2y₂      £ -1,

y₁ – y₂ + y₃ £ -3,

               y₃ £ 0.

 

 

Решение исходной задачи находим симплексным методом (табл. 1.2).

i	Базис	С базиса	A0	0	1	0	-1	-3	0
				A1	A2	A3	A4	A5	A6
1 2 3	A1 A3 A6	0 0 0	1 2 5	1 0 0	2 -4 3	0 1 0	-1 2 0	1 -1 1	0 0 1
m + 1	Zi - Cj		0	0	-1	0	1	3	0
1 2 3	A5 A3 A6	-3 0 0	1 3 4	1 1 -1	2 -2 1	0 1 0	-1 1 1	1 0 0	0 0 1
m + 1	Zi - Cj		-3	-3	-7	0	4	0	0
1 2 3	A5 A4 A6	-3 -1 0	4 3 1	2 1 -2	0 -2 3	1 1 -1	0 1 0	1 0 0	0 0 1
m + 1	Zi - Cj		-15	-7	1	-4	0	0	0
1 2 3	A5 A4 A2	-3 -1 1	4 11/3 1/3	3 -1/3 -2/3	0 0 1	1 1/3 -1/3	0 1 0	1 0 0	0 2/3 1/3
m + 1	Zi - Cj		-46/3	-19/3	0	-11/3	0	0	-1/3

 

Оптимальный план исходной задачи X* = (0; 1/3; 0; 11/3; 4; 0), при котором Z_min = - 46/3, получен в четвертой итерации табл. 1.2. Используя эту итерацию, найдем оптимальный план двойственной задачи. Согласно теореме двойственности оптимальный план двойствен­ной задачи находится из соотношения Y* = C*D ^-1 , где матрица D ^-1 - матрица, обратная матрице, составленной из компонент векторов, вхо­дящих в последний базис, при котором получен оптимальный план исходной задачи. В последний базис входят векторы A₅, A₄, A₂; значит,

                              1 -1 2

D = ( A₅, A₄, A₂ ) = -1 2 -4

                              1 0    3

Обратная матрица D ^-1 образована из коэффициентов, стоящих в столбцах A₁, A₃, A₆ четвертой итерации:

 

 

           2  1  0

D^-1 =     -1/3 1/3 2/3

        -2/3 -1/3 1/3

Из этой же итерации следует С* = (— 3; —1; 1). Таким образом

                                                             2  1  0

                Y = С* D^-1 = (-3; -1; 1) · -1/3 1/3 2/3

                                                          -2/3 -1/3 1/3

Y*=(-19/3; -11/3; -1/3),

т. е. y _i = С*Х _i, где Х _i — коэффициенты разложения последней ите­рации, стоящие в столбцах векторов первоначального единичного базиса.

Итак, i-ю двойственную переменную можно получить из значения оценки (m + 1)-й строки, стоящей против соответствующего вектора, входившего в первоначальный единичный базиc, если к ней приба­вить соответствующее значение коэффициента линейной функции:

у ₁ = — 19/3 + 0 = — 19/3; y₂ = -11/3 + 0 = -11/3; у ₃ = -1/3+0 = -1/3. При этом плане max f = -46/3.