 |
Главная |
Формулы Крамера для решения СЛАУ
|
из
5.00
|
Матричный способ решения СЛАУ, формулы Крамера, свойство присоединенной матрицы и основное свойство линейной зависимости.
Рассмотрим систему линейных алгебраических уравнений (СЛАУ), содержащую
т уравнений и п неизвестных:
 (1)
(1)
Пусть

– матрица коэффициентов при неизвестных, столбец свободных членов (чисел стоящих справа от равенства в системе (1)) и столбец неизвестных соответственно системы (1). Матрица А называется основной матрицей системы (1). Тогда очевидно, что система (1) может быть кратко записана в матричной форме  . Форма (1) называется координатной записью системы. Если
. Форма (1) называется координатной записью системы. Если  , т.е. число уравнений равно числу неизвестных, то СЛАУ называется «квадратной», она принимает вид:
, т.е. число уравнений равно числу неизвестных, то СЛАУ называется «квадратной», она принимает вид:
 (2)
(2)
Если же матрица А к тому же не вырождена, т.е.  , то тогда СЛАУ (2) можно решить как матричное уравнение
, то тогда СЛАУ (2) можно решить как матричное уравнение  по формуле
по формуле
 . (3)
. (3)
Этот метод называется матричным способом решения СЛАУ (2). 
Пример. Решить систему матричным способом, если это возможно:

Решение. Запишем эту систему как матричное уравнение  , где
, где
 ,
, 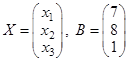 . Вычисляем:
. Вычисляем: 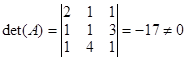 , следовательно, матричный способ применим. Находим обратную матрицу:
, следовательно, матричный способ применим. Находим обратную матрицу:

Следовательно,
 .
.
Ответ: 
Формулы Крамера для решения СЛАУ
Эти формулы применимы для решения СЛАУ при тех же условиях, что и матричный способ, а именно, когда матрица А коэффициентов при неизвестных этой СЛАУ квадратная и не вырожденная. Для нахождения неизвестных квадратной системы (2) надо вычислить главный определитель  , убедиться что
, убедиться что  , и затем вычислить п вспомогательных определителей
, и затем вычислить п вспомогательных определителей 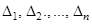 , где определитель
, где определитель  (
(  ) получается из главного определителя заменой в нем k-го столбца на столбец В свободных членов:
) получается из главного определителя заменой в нем k-го столбца на столбец В свободных членов:

Тогда решением системы (2) будет: 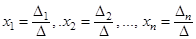 .
.
Вывод формул Крамера. Распишем подробно формулу (3)  .
.
Вспомним, что  , где
, где  – алгебраическое дополнение элемента
– алгебраическое дополнение элемента  , равное
, равное  , а
, а  – определитель порядка
– определитель порядка  , полученный из главного определителя D вычеркиванием i-й строки и j-го столбца. Получим
, полученный из главного определителя D вычеркиванием i-й строки и j-го столбца. Получим
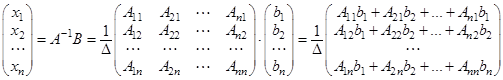 .
.
Итак, матричный способ дает формулу
 (4)
(4)
Сравним эту формулу с выражением для  , полученным по формуле Крамера:
, полученным по формуле Крамера:
 . (5)
. (5)
Заметим, что у всех элементов k-го столбца этого определителя алгебраические дополнения точно такие же, как и у элементов k-го столбца матрицы А. Поэтому, разложив определитель в (5) по этому столбцу, получим:
 . (6)
. (6)
Полученная формула (6) в точности совпадает с (4). Формулы Крамера доказаны.
Пример. Решить систему  методом Крамера, если это возможно:
методом Крамера, если это возможно:
Решение. Вычислим главный определитель системы:  , следовательно, метод Крамера применим. Далее вычислим три вспомогательных определителя:
, следовательно, метод Крамера применим. Далее вычислим три вспомогательных определителя:

Следовательно,  .
.
Дополнение 1. При выводе на лекции в ауд. 220 формулы для обратной матрицы через алгебраические дополнения использовалось основное свойство присоединенной матрицы
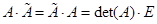 .
.
Доказательство этого свойства, в свою очередь, опиралось на два свойства определителя:
(1) Сумма произведений элементов произвольной строки квадратной матрицы на соответствующие алгебраические дополнения этой же строки равна определителю этой матрицы (и аналогично для столбцов):
 (разложение по i-й строке),
(разложение по i-й строке),
 (разложение по j-му столбцу)
(разложение по j-му столбцу)
(2) Сумма произведений элементов произвольной строки квадратной матрицы на соответствующие алгебраические дополнения другой строки равна нулю (и аналогично для столбцов):
 , (для строк, при
, (для строк, при  ),
),
 (для столбцов, при
(для столбцов, при  )
)
Свойство (1) нам известно из общих свойств определителя, которые у нас идут без доказательства. Среди этих свойств есть, в частности, такое:
если в определителе две строки или два столбца совпадают, то он равен нулю.
Теперь докажем свойство (2). Заменим в определителе 
j- строку на строку с номером i. Понятно что после этого у полученного определителя  две одинаковые строки, и потому он равен нулю. Заметим также, что алгебраические дополнения изменённой j-й строки не изменились, т.к. они не зависят от элементов этой строки. Разложим определитель
две одинаковые строки, и потому он равен нулю. Заметим также, что алгебраические дополнения изменённой j-й строки не изменились, т.к. они не зависят от элементов этой строки. Разложим определитель  по j-й строке, получим:
по j-й строке, получим:

Аналогично доказывается для столбцов.
Дополнение 2. Относительно линейной зависимости векторов теории линейного пространства, просьба не путать:
Общий критерий линейной зависимости векторов произвольного линейного пространства: Совокупность векторов линейно зависима тогда и только тогда, когда один из векторов выражается в виде линейной комбинации остальных.
Основное свойство линейной зависимости: Пусть даны n векторов линейного пространства 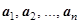 , и еще какие-то т векторов этого же пространства,
, и еще какие-то т векторов этого же пространства, 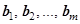 каждый из которых линейно выражается через
каждый из которых линейно выражается через 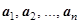 , причем,
, причем,  . Тогда векторы
. Тогда векторы 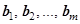 линейно зависимы.
линейно зависимы.
Доказательство этого свойства есть в лекциях, присланных на вашу Почту.
|
из
5.00
|
Обсуждение в статье: Формулы Крамера для решения СЛАУ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

