 |
Главная |
характеристик пространственных квазипериодических структур
|
из
5.00
|
Лазерная система для измерения статистических
Введение
В последние годы наблюдается интенсивное развитие аэрокосмической и ракетной техники, что в свою очередь ставит перед промышленностью задачу создания точных и надежных систем связи, ориентации и обнаружения подвижных объектов в пространстве. В большинстве случаев данные задачи решаются с применением радиолокационных СВЧ систем. Одним из важных звеньев этих систем является генератор СВЧ электромагнитных волн, качество которого обеспечивает надежность и тактико-технические характеристики СВЧ систем в целом.
Производство СВЧ приборов является экономически дорогостоящим и технологически трудоемким из-за использования дорогостоящих и труднообрабатываемых материалов. Наиболее трудоемким процесом является изготовление и контроль качества линий замедления (ЛЗ) к магнетронным и клистронным генераторам.
ЛЗ представляют собой пространственные периодические структуры типа оптических дифракционных решеток, точностью которых определяются радиотехнические параметры СВЧ генератора. При этом задача метрологического контроля геометрических размеров ЛЗ по своей трудоемкости и затратам соизмерима со временем и трудоемкостью ее изготовления.
Традиционные методы контроля геометрических параметров ЛЗ с помощью визуальных оптических приборов являются не произво-дительными и трудоемкими, автоматизация которых сложна и непе-респективна. Поэтому очень важной для метрологического обеспечения производства СВЧ систем становится создание высокопроизводительных методов и средств контроля геометрических размеров ЛЗ, и в первую очередь - статистических размеров элементов ее пространственной переодической структуры. Эта задача является актуальной и диктуется реальными потребностями производства.
Благодаря увеличившемуся прогресу в области вычислительной техники и информатики становится возможным и даже необходимым применение возможностей, открывающихся перед разработчиком. Я имею в виду создание автоматизированных измерительных систем контроля качества. Эти системы используя вычислительную мощь современной техники позволят продуктивно перераспределить трудовые ресурсы и существенно повысить продуктивность труда с одновременным снижением себестои-мости выполняемых работ. Для такой системы не требуется высокая квалификация и не важен опыт работы. Измерительная система берет на себя все рутинные операции измерения и вычисления, а оператор только руководит процесом измерения. В результате такая система оказывается экономически оправданной, так как персонал может быть обучен в течении двух дней - одной недели, в зависимости от способностей.
В данной работе производится проектирование и разработка автоматизированной измерительной системы контроля качества изготовления ЛЗ на базе ПЗС-приемника и с применением ЭВМ. С помощью современной ЭВМ возможно не только обработать информацию и получить статистические характеристики, но и отобразить их на экране монитора в удобной для понимания форме. Будут преставлены: математи-ческая модель измерительной системы, произведены габаритный и энергетический расчеты, функциональная схема системы.
1. Существующие методы и средства геометрического
контроля периодических пространственных структур
Из существующих средств для контроля геометрических размеров пространственных структур наиболее широко в промышленности используются микроскопы, проекторы и фотоэлектрические измерительные оптические приборы (фотоэлектрические микроскопыи лазерные дифрактометры ). Но для геометрического контроля пространственной структуры ЛЗ в настоящее время прромышленно используют лишь микроскопы и проекторы. Существенным недостатком применения этих приборов является значительная трудоемкость всего метрологического процесса, а также необходимость статистической обработки результатов измерения размеров a и b ЛЗ.
Более переспективным для автоматизации геометрического контроля ЛЗ является применение фотоэлектрических измерительных приборов, выполненных на основе лазерных дифрактометров. Однако для автомати-зации геометрического контроля ЛЗ в настоящее время лазерные дифрактометры пока еще мало используются из-за отсутствия их промыш-ленного производства.
1.1. Контроль с помощью микроскопов
Контроль статистических характеристик геометрических размеров a и b квазипериодической структуры ЛЗ в промышленных условиях осуществляют с помощью микроскопов УИМ-21, МИМ-3, МБС-1, МИС-1, МБИ-14.
Применение микроскопов позволяет визуально контролировать не только все размеры элементов квазипериодической структуры ЛЗ, но и качество поверхности, ее шероховатость и структуру, наличие мелких заусенцев и другие дефекты поверхности.
Дефекты обработки материалов контролируют при помощи стерео-скопического микроскопа МБС-1. Этот микроскоп позволяет наблюдать прямое и объемное изображение объекта, как в проходящем, так и в отраженном свете, обеспечивая 3.5х - 88х увеличение.
Универсальные микроскопы УИМ-21 и МИМ-3 позволяют с точностью до 1 мкм выполнять контроль геометрических размеров элементов квази-периодической структуры ЛЗ различных типов. Во всех случаях измерения размеров a и b элементов структуры ЛЗ выполняется визуально оператором-метрологом ОТК, а результаты оформляют в виде таблиц. На основе статистической обработки этих таблиц определяют математические ожидания и дисперсии размеров a и b ЛЗ, по которым выдается заключение о качестве изготовленной ЛЗ.
Однако, методы визуального геометрического контроля размеров структуры ЛЗ с помощью микроскопов обладают рядом существенных недостатков:
· результаты измерений сильно зависят от уровня подготовки опера-торов, т.е. сказывается влияние субъективного фактора;
· физиологическая утомляемость операторов значительно снижает точность и достоверность измерений;
· весь процесс контроля трудоемок, низкая производительность труда, необходимо выполнить большое количество вычислений при статис-тической обработке результатов измерений;
· длительная и ежедневная работа с микроскопом сильно ухудшает зрение контролеров ОТК;
· практическая сложность эффективной автоматизации процесса контроля.
Указанные выше недостатки частично устранены в методах контроля ЛЗ с помощью проекторов и эпидиаскопов.
1.2. Контроль с помощью проекторов
С помощью проекторов удобно контролировать граничные линии элементов квазипериодической структуры ЛЗ. Изменяя кратность увели-чения прибора можно просматривсть отдельные участки, либо в целом всю структуру ЛЗ. Максимальное увеличение, серийно выпускаемых отечест-венной промышленностью проекторов, достигает 200 х, что позволяет определить погрешности изготовления элементов квазипериодической структуры ЛЗ порядка 4 мкм.
Для повышения производительности процесса и осуществления комплексного контроля сравнивают спроецированный контур ЛЗ с так называемым “белком” - чертежом ЛЗ в увеличенном масштабе на экране с координатной сеткой для измерения величины размеров a и b. В условиях серийного производства ЛЗ для улучшения сохраняемости и исключения деформации чертежа взамен “белков” применяют их фотошаблоны, выполняемые на стекле.
Для изготовления фотошаблона засвечивают и проявляют фото-пластинку, на которой затем тонким резцом почерчивают профиль ЛЗ в требуемом масштабе. С целью обеспечения высокой точности, эту операцию выполняют на координатно-расточном станке. Из полученного негатива изготавливают печатным способом диапозитивные изображения ЛЗ на стекле.
Контроль ЛЗ с помощью проекторов является более высоко-производительным, чем с помощью микроскопов, а также меньше влияет на зрение контролеров-операторов ОТК. Но ему присущи существенные недостатки, среди которых главным является практическая сложность автоматизации процесса контроля. В процессе контроля возникает также необходимость статистической обработки результатов измерений для определения СКО 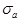 и
и 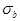 размеров a и b.
размеров a и b.
Поэтому в условиях серийного производства ЛЗ на первый план метрологического обеспечения их контроля выходит проблема создания измерительных систем для контроля статистических характеристик размеров a и b структуры ЛЗ. Они по своему принципу действия являются фотоэлектрическими измерительными приборами и могут быть построены на базе сканирующих фотометрических микроскопов, либо лазерных дифрактометров. Практическое применение этих систем должно обес-печивать:
· сокращение времени измерения размеров a и b, а также времени на их статистическую обработку;
· устранение влияния уровня подготовки метрологов на надежность процесса крнтроля:
· повышение достоверности измерения размеров a и b путем их измерения в нескольких сечениях на высоте h зубьев ЛЗ;
· снижение уставаемости зрения оператора-метролога ОТК.
1.3. Измерительный автомат “Bugs” для контроля
периодичности спиралей ламп бегущей волны
В 70-х годах фирмой “Bugs” (США) был разработан измерительный автомат для контроля периода навивки спиралей ламп бегущей волны (ЛБВ). Использование этого автомата позволило сократить время контроля периодичности навивки спиралей ЛБВ с двух человеко-дней до десяти минут.
В основу работы автомата положен теневой оптический метод последовательного сканирования всех элементов изделия и сравнения их с эталоном. Для достижения высокой точности измерений перемещение контролируемого изделия в поле зрения оптической системы осуществ-ляется гидравлическими приводами.
Точность измерений прибора не зависит от скорости перемещения спирали. Однако вибрации контролируемого изделия, а также деталей всего прибора недопустимо и устраняется применением системы сложных гидравлических приборов. Кроме того, необходима также высокая точность фокусировки оптической системы, нарушение которой приводит к размытию изображения. Так как существует ряд деталей которые перемещаются друг относительно друга, то необходима механическая прецизионная система, что усложняет конструкцию прибора и повышает соответсвенно его стоимость.
В последующие годы конструкция аппарата была модернизирована и улучшены его метрологические характеристики. Но следует отметить, что производительность этого аппарата не может быть существенно увеличена из-за использования в нем теневых оптических методов измерений, возможности которых в данном случае уже исчерпаны, поскольку необходим последовательный просмотр всех элементов пространственной структуры. К недостаткам прибора следует отнести необходимость использоваия системы сложных гидравлических приводов для виброзащиты спирали.
Указанные недостатки частично устранены в фотоэлектрических измерительных микроскопах, которые также могут быть использованы для контроля геометрических размеров элементов ЛЗ.
1.4. Фотоэлектрические сканирующие микроскопы
В работе [24] описана опытно-конструкторская разработка фотоэлект-рического микроскопа ФЭМ-2, предназначенного для геометрического контроля размеров малых объектов. В основу работы микроскопа положено формирование оптической системой увеличенного солинейного изображения измеряемого объекта. В плоскости изображения расположен фотоприемник, выходной сигнал которого поступает на электро-измерительную аппаратуру. К недостаткам этого прибора следует отнести отсутствие коррекции дрейфа “нуля”, малый предел фото-электрических измерений ( до 10 мкм ), ручное управление процессом измерений и окулярный отсчет показаний прибора, что не позволило использовать его в промышленных условиях для геометрического контроля ЛЗ.
Указанные недостатки частично устранены в фотоэлектрическом микроскопе ФЭМ-1Ц [25], который предназначен для измерений линейных размеров малых объектов величиной £ 100 мкм. При этом дискретность отсчетов составляет 0.5 мкм, а максимальная погрешность измерений не более ± 0.3 мкм. Этот микроскоп в бывшем СССР серийно выпускался с 1980 года. В качестве выходного индикатора в нем используется цифровая отсчетная система. Одним из основных недостатков микроскопа ФЭМ-1Ц является малое быстродействие - время автомати-ческого наведения на штрих до 20 с, зависимость погрешности измерений от качества фокусировки оптической системы, что требует практически непрерывного визуального контроля качества изображения в окуляр при измерении длиномерных объектов. Электронная система микроскопа не позволяет выполнять статистическую обработку резудьтатов измерений. В силу указанных недостатков они не нашли применеия для геометрического контроля структуры ЛЗ.
1.5. Лазерные дифракционные измерители
линейных размеров малых объектов
Предположения о возможности использования явления дифракции световых волн для контроля размеров малых объектов были впервые высказаны Роулэндом в 1888 году [13, 14, 15]. Позже он использовал это для качественного контроля изготовления периодической структуры дифракционных решеток. Сущность метода заключалась в том, что, если дифракционную решетку осветить монохроматической световой волной, то на некотором растоянии от нее формируются эквидистантно располо-женные дифракционные максимумы светового потока. При наличии дефек-тов решетки, вокруг этих основных максимумов возникают и добавочные максимумы, которые получили название “духов”. Однако теоретическое обоснование этого явления в то время так и не было сформулировано, что и не позволило определить аналитические зависимости, описывающие функциональную взаимосвязь распределения светового потока в “духах” с дефектами решетки.
Большой вклад в развитие теории дифракционных решеток внес В. Рон-ки, который занимался развитием и совершенствованием их производства более пятидесяти лет, начиная с 1921 года [13, 26]. Он дал простейшую теорию дифракционных решеток, описал их основные свойства и возмож-ность применения для контроля характеристик фотографических объек-тивов.
Г.Харисон [27] в 1949 году предложил способ контроля дифракционных решеток с помощью интерферометра Майкельсона и положил, таким образом, начало разработке схемы интерферометра с дифракционной решеткой для контроля качества самих решеток.
Дифракционные методы контроля качества изготовления периодических структур являются наиболее переспективными. Они положены в основу многочисленных лазерных дифракционных измерителей линейных размеров малых объектов.
Для контроля диаметра тонких отверстий в [28] предложено освещать контролируемые отверстия монохроматической световой волной и измерять амплитуду четных и нечетных максимумов дифракционной картины отверс-тия. Для расширения диапазона диаметра измеряемых отверстий, необхо-димо изменять длину волны 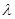 излучения до тех пор, пока амплитуда интерференционного сигнала нечетных гармоник достигнет удвоенного значения амплитуды световой волны в свободном пространстве. Диаметр измеряемого отверстия определяют по формуле :
излучения до тех пор, пока амплитуда интерференционного сигнала нечетных гармоник достигнет удвоенного значения амплитуды световой волны в свободном пространстве. Диаметр измеряемого отверстия определяют по формуле : 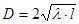 , где
, где 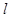 - растояние между измеряемым отверстием и точкой измерения светового поля в дифракционной картине. Недостатком метода является необхо-димость применения лазера с перестраиваемой длиной волны генерации.
- растояние между измеряемым отверстием и точкой измерения светового поля в дифракционной картине. Недостатком метода является необхо-димость применения лазера с перестраиваемой длиной волны генерации.
Известны также устройства [29, 30] для допускового контроля геометрических размеров изделий путем соответствующей обработки их дифракционного изображения сложной фотоэлектрической измерительной системой, либо оптической системой пространственной фильтрации. Однако эти устройства являются узко специализированными и требуют предварительного синтеза сложных голографических пространственных фильтров, что позволяет их использовать лишь для качественного допус-кового контроля изделий.
Таким образом лазерные дифрактометры являются наиболее переспек-тивным научным направлением развития автоматизированного метро-логического оборудования. Оно может быть также успешно использовано и для разработки средств автоматизации контроля статистических характе-ристик квазипериодической структуры ЛЗ. Это, в свою очередь, может быть выполнено лишь с созданием специализированных оптических систем обработки изображений (ОСОИ) на базе когерентных оптических спектро-анализаторов (КОС) пространственных сигналов, положенных в основу практически всех известных лазерных дифрактометров.
2. Обзор схем построения лазерных
дифрактометров
Интенсивное развитие этих систем началось в начале 80-х годов. Построение голографических и дифракционных оптических систем для метрологии основано на получении изображений Френеля, либо Фурье исследуемого объекта с последующим анализом их параметров фото-электической измерительной системой.
Основным преимуществом таких метрологических систем, перед ви-зуальными оптическими измерительными приборами, является высокая производительность, что позволяет автоматизировать ряд метрологических процессов в промышленности. Где требуется интегральная комплексная оценка качества изделия.
Для формирования изображений Фурье или Френеля исследуемого объекта используют когерентный оптический спектроанализатор прост-ранственных сигналов, схему построения и геометрические параметры которого выбирают в зависимости от характера решаемой задачи.
В настоящее время уже стала классической схема когерентного оптического спектроанализатора (КОС), приведенная на рис.1.
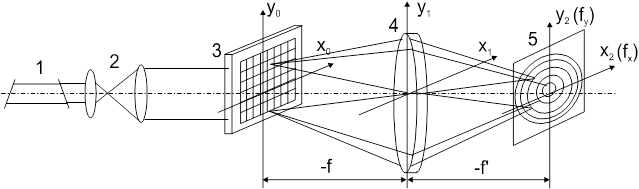
Рис.1. Принципиальная схема когерентного оптического спектро-
анализатора:
1. Лазер;
2. Телескопическая схема Кеплера;
3. Входной транспарант;
4. Фурье-объектив;
5. Дифракционное изображение.
КОС состоит из расположенных последовательно на одной оптической оси источника когерентного излучения - лазера 1 и телескопической систе-мы 2 Кеплера, формирующей плоскую когерентную световую волну. Эта волна падает на входной транспарант 3 с фотографической записью исследуемого сигнала. Входной транспарант 3 расположен в передней фокальной плоскости фурье-объектива 4 (объектива свободного от аберра-ции дисторсии и поперечной сферической ) с фокусным растоянием 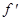 . На входном транспаранте 3 световая волна дифрагирует, и фурье-объективом 4 в задней плоскости 5 формируется дифракционное изображение исследуемого сигнала, которое является его фурье-образом и описывается выражением
. На входном транспаранте 3 световая волна дифрагирует, и фурье-объективом 4 в задней плоскости 5 формируется дифракционное изображение исследуемого сигнала, которое является его фурье-образом и описывается выражением
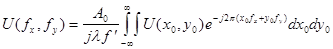 , где А0 -амплитуда плос-кой монохроматической световой волны в плоскости
, где А0 -амплитуда плос-кой монохроматической световой волны в плоскости 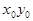 ;
; 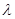 - длина волны;
- длина волны; 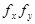 - пространственные частоты, равные
- пространственные частоты, равные 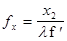 и
и 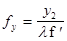 , где х2, у2 - пространственные координаты в плоскости 5.
, где х2, у2 - пространственные координаты в плоскости 5.
Таким образом, распределение комплексных амплитуд световых полей в задней и передней плоскостях фурье-объектива 4 оптической системы связаны между собой парой преобразований Фурье. Поле в задней фокальной плоскости является пространственным амплитудно-фазовым спектром сигнала, помещенного в его передней фокальной плоскости.
Описанная выше оптическая система выполняет спектральное разложе-ние пространственного сигнала и является когерентным оптическим спектроанализатором. Он позволяет анализировать одновременно ампли-тудный и фазовый спектры как одномерных, так и двумерных пространст-венных сигналов.
Существует две основные разновидности схем построения лазерных дифрактометров. Эти схемы представлены на рис .2 и рис. 3.
При условии фокусировки оптической системы, представленной на рис.2, в ней осуществляется спектральное преобразование Фурье, форми-руемое в плоскости х3у3, над сигналом помещенным во входной плоскости х1у1. Однако, фурье-образ сигнала в такой системе содержит квадратичную модуляцию фазы волны из-за наличия фазового сомножителя, стоящего перед интегралом в выражении :
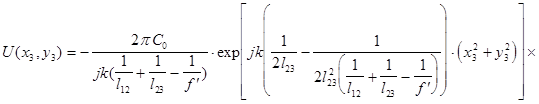
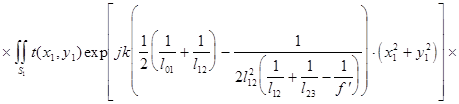
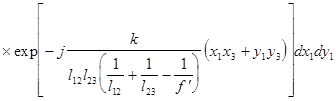 (2.1).
(2.1).
Это выражение описывает пространственное распределение комплекс-ных амплитуд светового поля в плоскости х3у3 спектрального анализа и со-держит ряд взаимонезависимых квадратичных фазовых сомножителей.
Наличие фазовой модуляции фурье-образа приводит к тому, что при ре-гистрации его методами голографии в результирующей интерферограмме возникают дополнительные аберрации, значительно влияющие на его ка-чество. Эта фазовая модуляция также имеет важное значение и не может быть опущена в случае дальнейших преобразований деталями оптической системы фурье-образа сигнала. Но эта модуляция может быть устранена при соответствующем выборе геометрических параметров оптической системы, т.е.
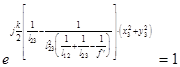 , при
, при 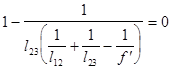 . (2.2).
. (2.2).
Таким образом, квадратическая фазовая модуляция фурье-образа устра-нима лишь в двух случаях:
· при размещении сигнального транспаранта в передней фокальной плоскости фурье-объектива, что полностью совпадает с полученными ранее результатами исследований, но лишь для КОС с плоской вол-ной во входной плоскости, т.е. при 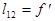 .
.
· при 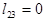 , т.е. плоскость х3у3 спектрального анализа должна совпа-дать с плоскостью х2у2 размещения фурье-объектива, что физически нереализуемо в оптической системе, согласно условию Гауса.
, т.е. плоскость х3у3 спектрального анализа должна совпа-дать с плоскостью х2у2 размещения фурье-объектива, что физически нереализуемо в оптической системе, согласно условию Гауса.
Учитывая выражения 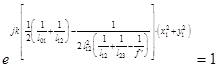 и (2.2) можем преобразовать (2.1) к виду:
и (2.2) можем преобразовать (2.1) к виду:
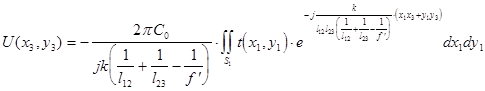 (2.3),
(2.3),
откуда видно, что квадратичные фазовые искажения фурье-образа сигнала устранимы не только при освещении входного транспаранта плоской, но и сферической волной.
При условии фокусировки оптической системы, показанной на рис.3, в ней осуществляется спектральное преобразование Фурье, формируемое в плоскости х3у3, над пространственным сигналом, помещенном в плоскости х2у2. Однако, фурье-образ сигнала в такой системе содержит квадра-тическую модуляцию фазы волны из-за наличия фазового сомножителя. Наличие фазовой модуляции фурье-образа сигнала приводит к допол-нительным аберрациям интерферограммы при регистрации методами голографии. Эта модуляция имеет также важное значение и не может быть опущена. Модуляция может быть устранена на оптической оси системы и при 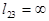 , т.е. при фокусировке оптической системы на бесконечность. Но в этом случае оптическая система не будет осуществлять спектральное преобразование Фурье.
, т.е. при фокусировке оптической системы на бесконечность. Но в этом случае оптическая система не будет осуществлять спектральное преобразование Фурье.
Для оптической системы КОС, представленной на рис.3, квадратичные фазовые искажения, приводящие к аберрационным искажениям фурье-об-раза сигнала, не могут быть устранены лишь путем соответствующего выбора геометрических парметров оптической системы. Для устранения этих искажений необходимо оптическую систему дополнить корректирую-щим фильтром с фазовой характеристикой, сопряженной к квадратичным фазовым искажениям фурье-образа сигнала.
Итак можно сделать выводы:
· Квадратичные фазовые искажения фурье-образа сигнала устранимы путем соответствующего выбора геометрических размеров оптичес-кой системы, но лишь для КОС, выполненного по схеме “входной транспарант - перед фурье-объективом”.
· При расположении ЛЗ в передней фокальной плоскости фурье-объектива масштаб ее дифракционного изображения не зависит от радиуса освещающей волны, а определяется величиной фокусного растояния и длиной волны излучения лазера. Это позволяет рас-ширить дифракционную полосу анализа путем увеличения радиуса освещающей волны, не изменяя, при этом масштаб дифракционного изображения.
· При освещении ЛЗ, расположенной в передней фокальной плоскости фурье-объектива, плоской световой волной, погрешность прост-ранственной частоты зависит лишь от длины волны излучения лазера и фокусного растояния фурье-объектива, что позволяет обеспечить ее уменшение путем увеличения 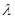 и
и 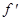 .
.
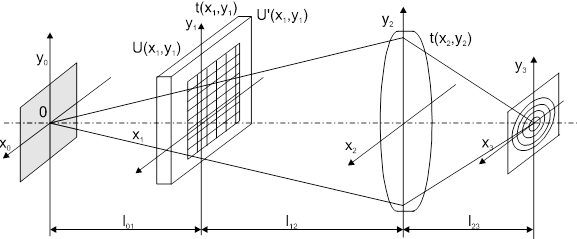
Рис.2. Схема КОС со входным транспарантом перед фурье-объективом
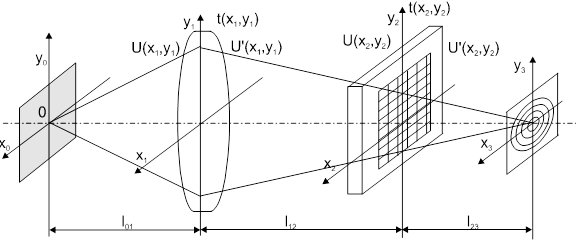
Рис.3. Схема КОС со входным транспарантом за фурье-объективом
3.Математическая модель квазипериодической
структуры СВЧ линий замедления
При статистических исследованиях геометрических размеров элементов пространственной структуры ЛЗ установлено, что из-за различных техноло-гических погрешностей, эти размеры являются величинами случайными с нормальным законом распределения. Таким образом, пространственная структура ЛЗ не является строго переодической, а поэтому ее энер-гетический спектр будет отличаться от энергетического спектра периоди-ческих структур.
Из скалярной теории [7, 8] известно, что оптической системой КОС в плоскости спектрального анализа формируется дифракционное изображе-ние пространственного объекта, помещенного во входной плоскости. Математические зависимости, описывающие форму дифракционного изоб-ражения, могут быть определены лишь путем решения задачи о дифракции когерентной световой волны на пространственной структуре объекта. Одна-ко для пространственной структуры ЛЗ с флуктуациями периодичности, решение такой задачи чисто оптическими методами не может быть полу-чено из-за значительной математической сложности ее. Кроме, того эти методы применимы лишь для решения дифракционных задач на регу-лярных детерминированных пространственных структурах и неприменимы для случайных пространственных сигналов.
Поэтому в настоящее время такие задачи для случайных оптических сигналов решают в оптике с применением методов статистической радио-физики в силу единства физических процессов и математических методов анализа прохождения электрических сигналов в электрических цепях и распостранения пространственных сигналов в оптических системах. Это позволяет определить распределение освещенности в дифракционном изображении квазипериодической пространственной структуры ЛЗ (т.е. ее энергетический спектр) путем вычисления усредненного квадрата преобра-зования Фурье над ее амплитудным коэфициентом пропускания.
Пространственная штриховая структура ЛЗ является квазипериодичес-ким сигналом, в технике ОСОИ, и состоит из взаимонезависимых прозрач-ных щелей и непрозрачных стенок. К тому же период пространственной структуры ЛЗ также является случайной величиной, так как он равен сумме двух взаимонезависимых величин. Таким образом, пространственная струк-тура ЛЗ относится к классу случайных квазипериодических сигналов.
Поскольку освещенность пространственной структуры ЛЗ, помещенной во входной плоскости КОС, равномерна по полю, то ее амплитудный коэфициент попускания 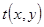 может быть описан единично-нулевой функ-
может быть описан единично-нулевой функ-
цией. Поэтому, в пределах ширины 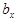 прозрачных щелей функция
прозрачных щелей функция 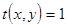 , а в пределах ширины
, а в пределах ширины 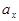 непрозрачных стенок, соответственно, 0. Кроме того, ширина щелей
непрозрачных стенок, соответственно, 0. Кроме того, ширина щелей 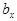 и стенок
и стенок 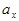 являются величинами взаимонезави-симыми, поскольку при изгибах стенок толщина
являются величинами взаимонезави-симыми, поскольку при изгибах стенок толщина 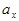 их не изменяется, а изменяется лишь ширина
их не изменяется, а изменяется лишь ширина 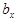 щелей. Взаимонезависимость этих величин также возникает и потому, что зубья в верхней и нижней гребенках наре-заются раздельно на разных заготовках, после спаивания которых обра-зуются между зубьями щели, а ширина их уже не зависит от толщины зубьев, что подтверждается также малостью коэфициента корреляции
щелей. Взаимонезависимость этих величин также возникает и потому, что зубья в верхней и нижней гребенках наре-заются раздельно на разных заготовках, после спаивания которых обра-зуются между зубьями щели, а ширина их уже не зависит от толщины зубьев, что подтверждается также малостью коэфициента корреляции 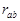 для размеров
для размеров 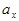 и
и 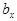 .
.
Фрагмент квазипериодической пространственной структуры ЛЗ и соот-ветствующая ему функция пропускания 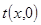 в сечении у=0 показаны на рис.4 (а и б), где Рх - период пространственной структуры, равный
в сечении у=0 показаны на рис.4 (а и б), где Рх - период пространственной структуры, равный 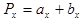 .
.
Поскольку ширина 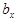 щелей и
щелей и 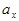 стенок являются величинами случайны-ми и взаимонезависимыми, то и период
стенок являются величинами случайны-ми и взаимонезависимыми, то и период 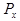 пространственной структуры ЛЗ будет также величиной случайной. Период
пространственной структуры ЛЗ будет также величиной случайной. Период 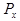 является суммой двух случай-ных величин с нормальными законами распределения, следовательно, закон распределения
является суммой двух случай-ных величин с нормальными законами распределения, следовательно, закон распределения 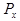 также будет нормальным.
также будет нормальным.
Таким образом, амплитудный коэфициент пропускания 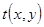 прост-ранственной квазипериодической структуры ЛЗ может быть описан функ-цией вида
прост-ранственной квазипериодической структуры ЛЗ может быть описан функ-цией вида
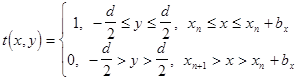 (2.4), где
(2.4), где 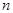 - порядковый номер щели,
- порядковый номер щели, 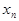 - пространственная координата положения начала щели,
- пространственная координата положения начала щели, 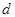 - высота перекрытия зубьев в квазипериодической структуре ЛЗ.
- высота перекрытия зубьев в квазипериодической структуре ЛЗ.
Из выражения (2.4) видно, что переменные х и у функции 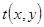 взаимо-независимы, а поэтому эта функция является функцией с разделяемыми переменными, и может быть представлена в виде произведения функций
взаимо-независимы, а поэтому эта функция является функцией с разделяемыми переменными, и может быть представлена в виде произведения функций 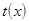 и
и 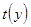 , т.е.
, т.е. 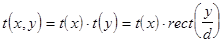 (2.5).
(2.5).
В выражении (2.5) функция 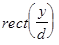 является финитной в пределах высо-ты
является финитной в пределах высо-ты 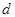 перекрытия зубьев верхней и нижней гребенок пространственной структуры ЛЗ вдоль координаты х, как показано на рис.4б.
перекрытия зубьев верхней и нижней гребенок пространственной структуры ЛЗ вдоль координаты х, как показано на рис.4б.
Для оптической системы КОС пространственная структура ЛЗ является квазипериодическим сигналом. В свою очередь, основными характеристи-ками такого сигнала, т.е. пространственной структуры ЛЗ, являются:
· средние размеры 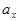 и
и 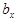 ширины стенок и щелей, а также средние квадратические отклонения СКО
ширины стенок и щелей, а также средние квадратические отклонения СКО 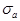 и
и 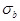 от них соответственно;
от них соответственно;
· законы распределения 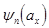 и
и 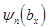 размеров стенок и щелей;
размеров стенок и щелей;
· спектральная и корреляционная функции.
Для описания спектральных и корреляционных функций случайных сигналов часто используются характеристические функции. Характеристи-ческая функция 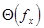 случайной величины
случайной величины 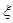 является фурье-образом ее закона распределения
является фурье-образом ее закона распределения 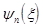 , т.е.
, т.е. 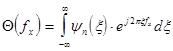 , где
, где 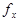 - простран-ственная частота, измеряемая в [мм-1], поскольку в рассматриваемом случае координата
- простран-ственная частота, измеряемая в [мм-1], поскольку в рассматриваемом случае координата 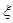 является пространственной и имеет размерность [мм].
является пространственной и имеет размерность [мм].
Тогда с учетом 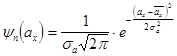 получим:
получим:
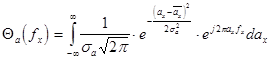 , а вводя замену переменных вида
, а вводя замену переменных вида
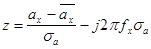 . Этот интеграл в новых пределах интегрирования от
. Этот интеграл в новых пределах интегрирования от 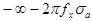 до
до 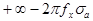 можно представить через элементарные функции следующим выражением
можно представить через элементарные функции следующим выражением
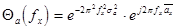 (2.6) , и аналогично
(2.6) , и аналогично 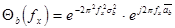 (2.7).
(2.7).
Полученные выражения (2.6) и (2.7) являются характеристическими функциями квазипериодической пространственной структуры ЛЗ с нормаль-ным законом распределения ширины 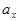 стенок и
стенок и 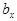 щелей.
щелей.
Как в оптических, так и в электронных устройствах спектрального анали-за сигналов, существует возможность получения как амплитудного, так и энергетического их спектров. Однако в теории спектрального анализа пространственных сигналов известно, что при использовании квадратичес-ких фотодетекторов для регистрации параметров дифракционного изобра-жения, формируемого оптической системой КОС, автоматически на ее вы-ходе формируется энергетический спектр исследуемого сигнала. Парамет-ры такого спектра могут быть измерены соответствующими контрольно-измерительными приборами, а форма его определена с применением мето-дов статистической радиооптики путем интегрального преобразования Винера-Хинчина, либо на основе теоремы Хилли.
Поэтому используя аналогию математических методов исследования спектральных характеристик пространственных и временных сигналов, распределение комплексных амплитуд спектра пропускания 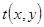 в дифракционном изображении пространственной квазипериодической струк-туры ЛЗ, можно определить как
в дифракционном изображении пространственной квазипериодической струк-туры ЛЗ, можно определить как 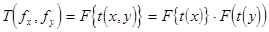 , или с уче-том (2.5)
, или с уче-том (2.5) 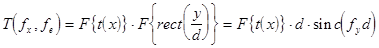 .
.
Полученное выражение описывает амплитудный спектр функции 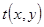 пропускания квазипериодической пространственной структуры ЛЗ. Энерге-тический спектр
пропускания квазипериодической пространственной структуры ЛЗ. Энерге-тический спектр 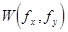 этой функции может быть определен с помощью теоремы Хилли [3.11] как
этой функции может быть определен с помощью теоремы Хилли [3.11] как 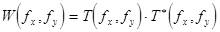 , или же
, или же
 .
.
Однако в работах [16, 17] показано, что для квазипериодического сигнала, описываемого единично-нулевой функцией вида (2.4)
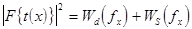 (2.8)
(2.8)
|
из
5.00
|
Обсуждение в статье: характеристик пространственных квазипериодических структур |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

